The derived subgroup, also known as the commutator subgroup, plays a crucial role in understanding the structure of a group by capturing elements generated from all commutators. This subgroup is essential for analyzing properties like solvability and normality within group theory. Explore the full article to deepen your knowledge of how the derived subgroup influences group behavior.
Table of Comparison
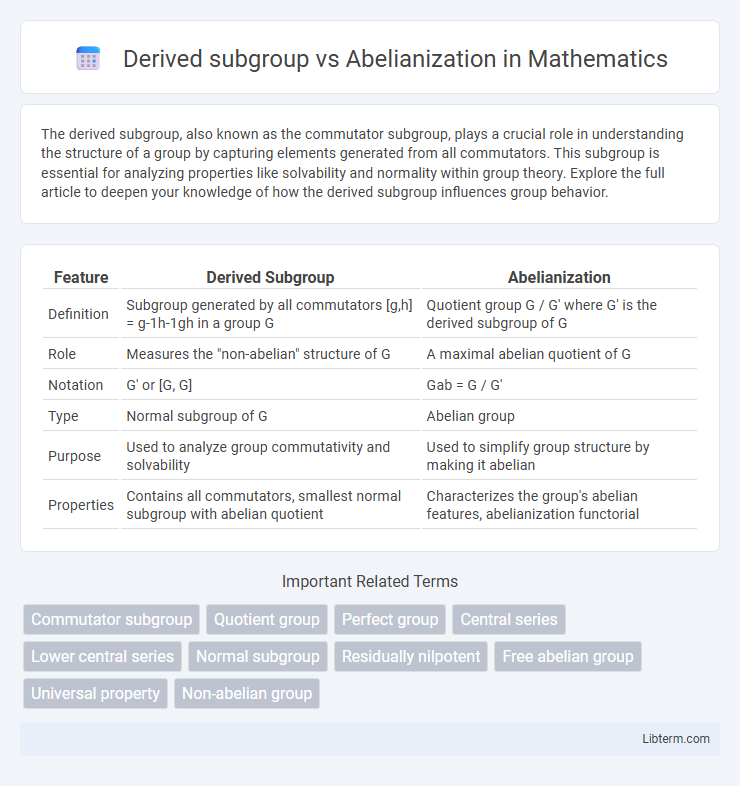
| Feature | Derived Subgroup | Abelianization |
|---|---|---|
| Definition | Subgroup generated by all commutators [g,h] = g-1h-1gh in a group G | Quotient group G / G' where G' is the derived subgroup of G |
| Role | Measures the "non-abelian" structure of G | A maximal abelian quotient of G |
| Notation | G' or [G, G] | Gab = G / G' |
| Type | Normal subgroup of G | Abelian group |
| Purpose | Used to analyze group commutativity and solvability | Used to simplify group structure by making it abelian |
| Properties | Contains all commutators, smallest normal subgroup with abelian quotient | Characterizes the group's abelian features, abelianization functorial |
Introduction to Derived Subgroup and Abelianization
The derived subgroup, also known as the commutator subgroup, is the subgroup generated by all commutators in a given group, capturing the group's non-abelian structure. Abelianization refers to the process of forming the largest abelian quotient group by dividing the original group by its derived subgroup. This construction efficiently measures how far a group is from being abelian by converting it into an abelian group.
Fundamental Definitions in Group Theory
The derived subgroup, or commutator subgroup, of a group G is generated by all commutators [x, y] = x^{-1}y^{-1}xy, capturing the subgroup that measures the non-abelian nature of G. Abelianization refers to the quotient group G/G', where G' is the derived subgroup, resulting in the largest abelian quotient of G that reflects the group's global commutative structure. These fundamental definitions link the internal structure of a group to its abelianized form by isolating elements responsible for non-commutativity through the derived subgroup.
Understanding the Derived Subgroup (Commutator Subgroup)
The derived subgroup, also known as the commutator subgroup, is generated by all commutators [g,h] = g-1h-1gh in a group G and captures the group's non-abelian behavior. Understanding the derived subgroup is crucial because it measures how far G is from being abelian; the smaller the derived subgroup, the closer G is to abelian. In contrast, the abelianization of G is the quotient group G/[G,G], which is always abelian and provides a canonical abelian approximation of G by modding out the derived subgroup.
Exploring Abelianization of a Group
The abelianization of a group G is the quotient group G/[G,G], where [G,G] is the derived subgroup or commutator subgroup generated by all commutators in G. This quotient transforms G into its largest abelian quotient, effectively measuring how far G is from being abelian by collapsing the commutator relations to the identity. Abelianization plays a crucial role in simplifying the study of groups by enabling the application of techniques and invariants from abelian group theory.
Key Differences between Derived Subgroup and Abelianization
The derived subgroup, also known as the commutator subgroup, is generated by all commutators in a group and measures the group's non-abelian nature by capturing elements that express non-commutativity. Abelianization is the quotient group formed by dividing the original group by its derived subgroup, effectively creating the largest abelian quotient. The key difference lies in that the derived subgroup is a specific subgroup within the group, while abelianization is a related factor group representing the group's abelian structure.
Algebraic Properties and Significance
The derived subgroup, also known as the commutator subgroup, is generated by all commutators and measures the extent to which a group fails to be Abelian, serving as a key tool in understanding a group's non-Abelian structure. Abelianization is the quotient group formed by dividing the original group by its derived subgroup, producing the largest Abelian quotient and simplifying the group's structure for analysis. These concepts are fundamental in algebra, with the derived subgroup capturing commutativity obstructions and Abelianization providing a canonical way to study groups through their Abelian images.
Applications in Group Structure Analysis
The derived subgroup, also known as the commutator subgroup, is crucial in measuring how far a group is from being Abelian by capturing all commutators, thus serving as a key tool in non-Abelian group analysis. Abelianization simplifies complex groups by factoring out the derived subgroup, resulting in an Abelian quotient that reveals information about the group's underlying abelian components and facilitates computations in homology and cohomology theories. Both constructions are fundamental in classifying finite groups, understanding normal series, and applying in algebraic topology and algebraic geometry, where the structure of fundamental groups or Galois groups is studied.
Examples Illustrating Derived Subgroup and Abelianization
The derived subgroup of a group \( G \), also known as the commutator subgroup \( G' \), consists of all finite products of commutators and measures how non-abelian the group is; for example, in the symmetric group \( S_3 \), the derived subgroup is the alternating group \( A_3 \), which is a normal subgroup of index two. Abelianization of \( G \) is the quotient group \( G/G' \), which is always abelian, capturing the "abelian essence" of \( G \); for \( S_3 \), the abelianization is isomorphic to the cyclic group \( C_2 \), reflecting that the quotient collapses all commutators to the identity. These examples highlight the relationship between the derived subgroup as a measure of non-commutativity and the abelianization as the universal abelian quotient, fundamental in group theory and its applications.
Interrelation and Exact Sequences
The derived subgroup, also known as the commutator subgroup, is the kernel of the abelianization homomorphism from a group \( G \) to its abelianization \( G^{ab} = G/[G,G] \), establishing an exact sequence \( 1 \to [G,G] \to G \to G^{ab} \to 1 \). This exact sequence highlights the interrelation that the derived subgroup measures the "non-abelianness" of \( G \) by capturing commutators, while the abelianization represents the maximal abelian quotient of \( G \). The process of abelianization thus factors through the derived subgroup, making the derived subgroup a normal subgroup that precisely records the kernel of the canonical surjective map to the largest abelian image.
Summary and Further Research Directions
The derived subgroup, also known as the commutator subgroup, is generated by all commutators and measures a group's non-abelian nature, while Abelianization is the quotient of the group by its derived subgroup, producing the largest abelian quotient. Research continues into the applications of derived subgroups in understanding group extensions, cohomology, and representation theory, as well as refining computational methods for Abelianization in complex group structures. Further inquiries explore connections with homological algebra and potential generalizations in non-classical algebraic systems.
Derived subgroup Infographic
 libterm.com
libterm.com