Homeomorphism is a fundamental concept in topology describing a continuous, bijective function with a continuous inverse between two spaces, signifying they are topologically equivalent. This means that one space can be transformed into the other without tearing or gluing, preserving properties like connectedness and compactness. Explore the rest of the article to understand how homeomorphisms classify shapes and spaces in mathematics.
Table of Comparison
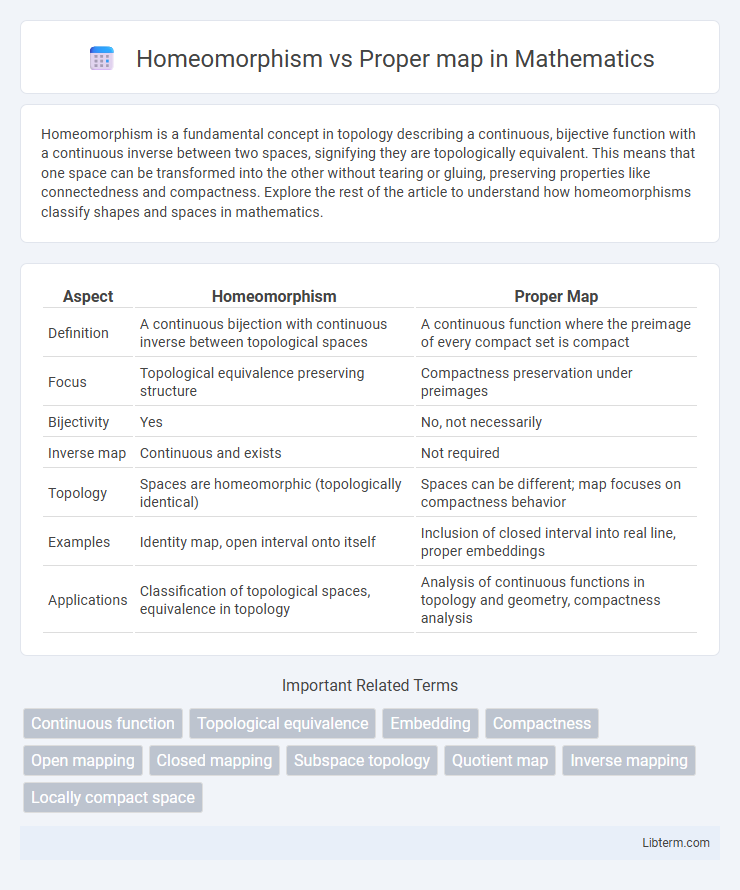
| Aspect | Homeomorphism | Proper Map |
|---|---|---|
| Definition | A continuous bijection with continuous inverse between topological spaces | A continuous function where the preimage of every compact set is compact |
| Focus | Topological equivalence preserving structure | Compactness preservation under preimages |
| Bijectivity | Yes | No, not necessarily |
| Inverse map | Continuous and exists | Not required |
| Topology | Spaces are homeomorphic (topologically identical) | Spaces can be different; map focuses on compactness behavior |
| Examples | Identity map, open interval onto itself | Inclusion of closed interval into real line, proper embeddings |
| Applications | Classification of topological spaces, equivalence in topology | Analysis of continuous functions in topology and geometry, compactness analysis |
Introduction to Homeomorphism and Proper Map
Homeomorphisms are bijective continuous functions with continuous inverses, preserving topological properties between spaces and establishing topological equivalence. Proper maps are continuous functions where the preimage of every compact set is compact, ensuring controlled behavior over infinite regions. Understanding these concepts aids in distinguishing between exact topological equivalences and continuous maps with compactness-preserving features.
Key Definitions: Homeomorphism Explained
A homeomorphism is a continuous, bijective function between topological spaces with a continuous inverse, preserving topological properties and enabling topological equivalence. Proper maps are continuous functions where the preimage of every compact set is compact, crucial in compactness arguments and manifold theory. Understanding homeomorphisms centers on their role in establishing topological sameness through invertible, structure-preserving mappings.
Key Definitions: Proper Map Unveiled
A proper map is a continuous function between topological spaces where the preimage of every compact set is compact, ensuring controlled behavior at infinity. Homeomorphisms are bijective continuous functions with continuous inverses, preserving topological structure exactly, but do not necessarily have the compactness preservation property inherent to proper maps. Proper maps generalize many compactness-related concepts in topology and are crucial for studying spaces with nontrivial boundary or growth conditions.
Fundamental Differences Between Homeomorphism and Proper Map
Homeomorphisms are continuous bijections with continuous inverses that establish topological equivalences between spaces, preserving all topological properties. Proper maps are continuous functions between topological spaces where the preimage of every compact set is compact, focusing on compactness behavior rather than bijectivity or invertibility. The fundamental difference lies in homeomorphisms being isomorphisms in the category of topological spaces, while proper maps emphasize the controlled behavior of compact sets and need not be bijective or invertible.
Topological Properties Preserved by Homeomorphism
Homeomorphisms preserve topological properties such as continuity, open and closed sets, connectedness, compactness, and the number of holes or genus in a space, making two spaces topologically equivalent. Proper maps, while maintaining compactness preimages of compact sets, do not guarantee the preservation of all topological invariants that homeomorphisms ensure. The key distinction lies in homeomorphisms being bijective continuous maps with continuous inverses, establishing a perfect topological equivalence.
Topological Properties Preserved by Proper Map
Proper maps preserve compactness, ensuring the preimage of every compact set remains compact, which is a crucial topological property distinct from homeomorphisms. Unlike homeomorphisms that preserve open sets and enable bijective continuous mappings with continuous inverses, proper maps focus on maintaining the structure of compact subsets through continuous functions. This distinction highlights proper maps' role in extending important topological invariants, such as compactness and closedness, across spaces without requiring bijections.
Examples Illustrating Homeomorphisms
Homeomorphisms are continuous bijections with continuous inverses that preserve topological properties, such as the unit circle \( S^1 \) being homeomorphic to any simple closed curve in the plane. Proper maps, by contrast, require the preimage of every compact set to be compact, exemplified by the map \( f: \mathbb{R} \to \mathbb{R}, f(x) = x^3 \), which is proper but not a homeomorphism due to failure of bijectivity. Classic examples highlighting homeomorphisms include the identity map on any topological space and the exponential map \( \exp: \mathbb{R} \to S^1 \) modulo \( 2\pi i \) showing quotient space homeomorphisms.
Examples Illustrating Proper Maps
Proper maps are continuous functions between topological spaces where the preimage of every compact set is compact, exemplified by the inclusion of a closed interval [0,1] into the real line R. Unlike homeomorphisms, which are bijective continuous maps with continuous inverses preserving topological structure exactly, proper maps need not be bijections but maintain compactness in inverse images, as seen in the map f: R - R defined by f(x) = x2 which is proper but not a homeomorphism due to lack of invertibility on R. These examples highlight how proper maps serve as key tools in topology for handling compactness, contrasting with homeomorphisms that emphasize structural equivalence.
Applications in Topology and Mathematics
Homeomorphisms serve as the foundation of topological equivalences, preserving open sets, continuity, and invertibility, thus enabling classification of spaces up to deformation. Proper maps, characterized by the preimage of compact sets being compact, play a crucial role in the study of non-compact spaces and manifold theory, ensuring controlled behavior at infinity. Applications in topology leverage homeomorphisms for identifying topological invariants, while proper maps facilitate compactification techniques and the extension of continuous functions.
Conclusion: Choosing the Right Concept for Your Problem
Homeomorphisms ensure a perfect one-to-one correspondence preserving topological structure, ideal for problems requiring equivalence between spaces. Proper maps guarantee preimages of compact sets remain compact, crucial in compactification and continuity considerations in non-compact spaces. Selecting between homeomorphisms and proper maps depends on whether structural equivalence or compactness properties are central to the problem's requirements.
Homeomorphism Infographic
 libterm.com
libterm.com