A simple module is a fundamental concept in abstract algebra where the module contains no submodules other than the trivial module and itself. This property makes simple modules essential building blocks in the study of module theory and representation theory. Explore the article to understand how simple modules influence the structure of more complex algebraic systems.
Table of Comparison
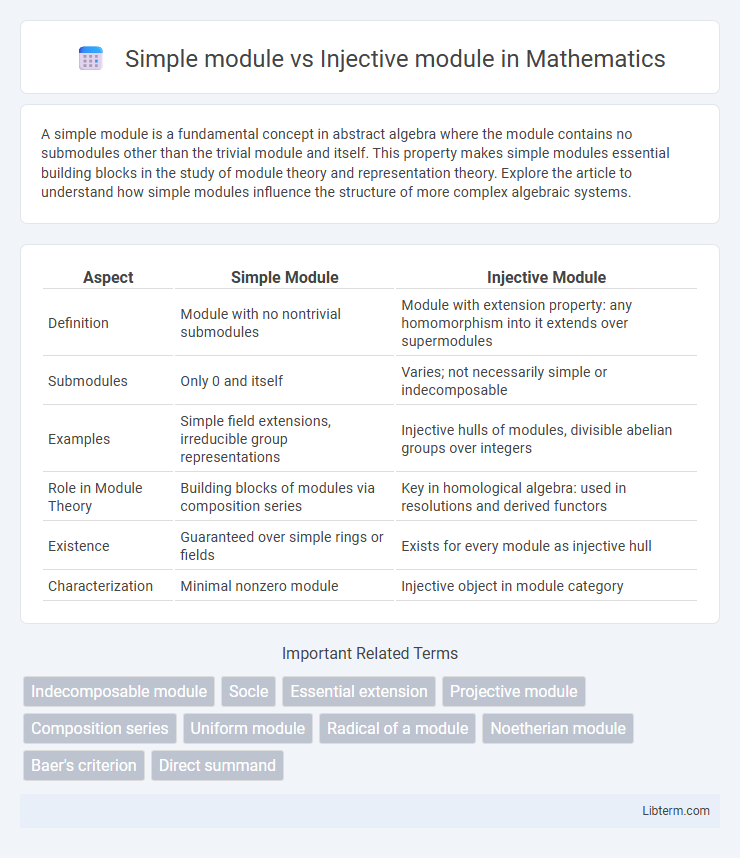
| Aspect | Simple Module | Injective Module |
|---|---|---|
| Definition | Module with no nontrivial submodules | Module with extension property: any homomorphism into it extends over supermodules |
| Submodules | Only 0 and itself | Varies; not necessarily simple or indecomposable |
| Examples | Simple field extensions, irreducible group representations | Injective hulls of modules, divisible abelian groups over integers |
| Role in Module Theory | Building blocks of modules via composition series | Key in homological algebra: used in resolutions and derived functors |
| Existence | Guaranteed over simple rings or fields | Exists for every module as injective hull |
| Characterization | Minimal nonzero module | Injective object in module category |
Introduction to Simple and Injective Modules
Simple modules are modules over a ring that contain no proper nonzero submodules, making them the building blocks of module theory through their irreducibility. Injective modules possess the property that every homomorphism from a submodule can be extended to the entire module, reflecting a form of module-theoretic completeness. Understanding simple and injective modules is fundamental in homological algebra and module classification.
Defining Simple Modules in Module Theory
Simple modules in module theory are modules that have no proper nonzero submodules, making them the building blocks for module decomposition. Unlike injective modules, which generalize the notion of divisible abelian groups and serve as essential extensions in exact sequences, simple modules represent minimal, indivisible structures. The categorization of simple modules plays a crucial role in understanding module homomorphisms and classification problems within algebra.
Characterizing Injective Modules
Injective modules are characterized by the property that every homomorphism from a submodule of any module can be extended to the entire module, distinguishing them from simple modules which contain no proper nontrivial submodules. Unlike simple modules that are minimal building blocks in module theory, injective modules often serve as essential tools in homological algebra due to their extension properties and their role in the characterization of injective hulls. Recognizing injective modules involves examining Baer's criterion, which asserts that a module is injective if and only if every homomorphism from an ideal of the ring to the module can be extended to the ring itself.
Key Differences: Simple vs Injective Modules
Simple modules contain no proper submodules besides zero, representing the smallest building blocks in module theory, whereas injective modules are defined by their property of extending homomorphisms from submodules to the entire module. Simple modules are characterized by minimality and irreducibility, while injective modules exhibit maximality in terms of embedding and homomorphism extension. The distinction lies in simplicity of structure versus the functional extension capability within module categories over a ring.
Examples of Simple Modules
Simple modules include examples such as the field \( \mathbb{F} \) viewed as a module over itself or the vector space \( \mathbb{F}^n \) under linear transformations where submodules correspond to subspaces. For instance, over a ring \( R \), simple modules are often isomorphic to \( R/I \) where \( I \) is a maximal ideal, such as the quotient \( \mathbb{Z}/p\mathbb{Z} \) for a prime \( p \) as a simple \(\mathbb{Z}\)-module. In contrast, injective modules like \( \mathbb{Q} \) as a \(\mathbb{Z}\)-module are characterized by their extension properties rather than minimality, highlighting the structural differences between simple and injective modules.
Examples of Injective Modules
Injective modules include important examples such as the Baer module over the ring of integers, which is an injective envelope of the integers as an abelian group, and divisible abelian groups like the rational numbers Q considered as Z-modules. Over fields, every vector space is both simple and injective since fields are simple rings. Another key example consists of injective modules over Noetherian rings, where injective hulls provide minimal injective extensions for modules like the direct sum of injective envelopes of simple modules.
Homomorphisms between Simple and Injective Modules
Homomorphisms from a simple module to an injective module are either zero or monomorphisms due to the simplicity of the domain, making every nonzero homomorphism injective. Injective modules exhibit the property that any homomorphism defined on a submodule, including the image of a simple module, extends to the entire module, ensuring rich morphism structures. The interplay between simple and injective modules often characterizes decomposition properties in module theory, leveraging homomorphism behavior to understand module embeddings and extensions.
Structural Properties and Implications
Simple modules exhibit a minimal structure with no proper nonzero submodules, providing a clear baseline for module decomposition. Injective modules extend this framework by possessing an essential extension property, allowing every module homomorphism into them to be extended from submodules to the entire module, which facilitates the classification of module categories and the solution of extension problems. The interplay between simple and injective modules underpins the characterization of semisimple rings and influences homological dimensions in module theory.
Applications in Algebra and Beyond
Simple modules serve as building blocks in module theory, essential for classifying modules through composition series and enabling the analysis of ring structures via the Jordan-Holder theorem. Injective modules facilitate solving extension problems, proving crucial in homological algebra for constructing injective resolutions and derived functors like Ext, which have applications in algebraic geometry and representation theory. Both types of modules underpin the structural study of algebraic systems and extend to fields such as category theory and functional analysis.
Summary and Conclusion
Simple modules are modules with no nontrivial submodules, representing the building blocks of module theory, while injective modules are characterized by their property that any homomorphism into them can be extended from submodules to the whole module. Simple modules are minimal and often used to classify modules via composition series, whereas injective modules serve as essential tools in homological algebra due to their extensibility and decomposition properties. Understanding the distinction highlights that simplicity concerns minimal structure, whereas injectivity involves an extension property critical for module decomposition and homological constructions.
Simple module Infographic
 libterm.com
libterm.com