Simple design emphasizes clarity and functionality, making it easier for users to navigate and understand content quickly. Minimalist elements reduce distractions, enhancing user experience and engagement. Explore the rest of the article to discover how simplicity can transform your projects effectively.
Table of Comparison
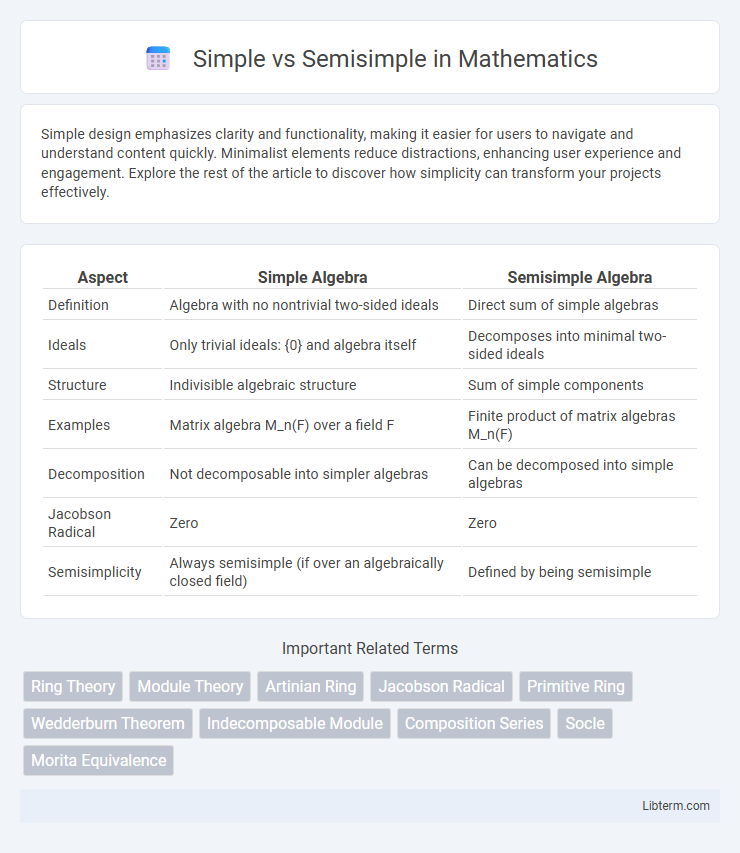
| Aspect | Simple Algebra | Semisimple Algebra |
|---|---|---|
| Definition | Algebra with no nontrivial two-sided ideals | Direct sum of simple algebras |
| Ideals | Only trivial ideals: {0} and algebra itself | Decomposes into minimal two-sided ideals |
| Structure | Indivisible algebraic structure | Sum of simple components |
| Examples | Matrix algebra M_n(F) over a field F | Finite product of matrix algebras M_n(F) |
| Decomposition | Not decomposable into simpler algebras | Can be decomposed into simple algebras |
| Jacobson Radical | Zero | Zero |
| Semisimplicity | Always semisimple (if over an algebraically closed field) | Defined by being semisimple |
Introduction to Simple and Semisimple Concepts
Simple algebraic structures feature no nontrivial ideals, ensuring indivisibility within ring or module theory. Semisimple entities decompose fully into direct sums of simple components, facilitating classification and analysis through their irreducible parts. This distinction underpins foundational approaches in representation theory and module decomposition, enabling effective study of algebraic systems.
Defining Simple Structures
Simple algebraic structures contain no nontrivial proper ideals, meaning their internal composition cannot be further decomposed or broken down, which is fundamental in ring theory and module analysis. Semisimple structures arise from direct sums of simple components, exhibiting complete reducibility and a rich decomposition, crucial in representation theory and module classification. Defining simple structures centers on their indivisibility and lack of nontrivial substructures, providing a baseline for understanding more complex algebraic forms.
Understanding Semisimple Structures
Semisimple structures, particularly in algebra, decompose into direct sums of simple components, allowing complex algebraic systems to be analyzed through their simpler, indivisible parts. Unlike simple structures, which contain no proper nontrivial ideals, semisimple objects exhibit complete reducibility and lack of radical elements, facilitating representation theory and module classification. This decomposition principle underpins key advancements in Lie algebras, group representations, and ring theory, highlighting the importance of understanding semisimple structures in modern mathematics.
Key Differences Between Simple and Semisimple
Simple algebraic structures contain no non-trivial proper ideals, representing indivisible building blocks in ring or module theory. Semisimple structures decompose into direct sums of simple components, allowing for complete reducibility and eliminating radical ideals. The fundamental difference lies in simplicity's strict indivisibility versus semisimplicity's structured decomposition into simple constituents.
Examples of Simple Objects
In category theory and algebra, simple objects are those with no nontrivial subobjects other than zero and themselves, exemplified by simple modules like the field of complex numbers viewed as a vector space over itself. For instance, in the category of vector spaces over a field, one-dimensional vector spaces serve as prime examples of simple objects since they contain no proper subspaces. These contrast with semisimple objects, which can be decomposed into direct sums of simple objects, illustrating the building blocks of more complex algebraic structures.
Examples of Semisimple Objects
Semisimple objects in algebra include semisimple modules such as finite-dimensional semisimple representations of groups, where each module decomposes into a direct sum of simple modules like irreducible representations of the symmetric group S_n. For instance, over a field, semisimple algebras decompose into direct sums of matrix algebras, such as the group algebra of a finite group being semisimple by Maschke's theorem. Another example involves semisimple Lie algebras, like \(\mathfrak{sl}_n(\mathbb{C})\), which decompose into simple components with no non-trivial ideals.
Importance in Algebra and Representation Theory
Simple and semisimple structures play a crucial role in algebra and representation theory by characterizing the building blocks of modules and algebras. Simple modules, having no nontrivial submodules, provide fundamental irreducible representations essential for understanding symmetry operations and group actions. Semisimple algebras decompose into direct sums of simple components, enabling classification of representations and facilitating computation of invariants in linear algebra and group theory.
Applications in Mathematics and Physics
Simple algebraic structures, such as simple Lie algebras, serve as fundamental building blocks in representation theory and particle physics by describing symmetry groups with no nontrivial normal subalgebras. Semisimple structures, composed of direct sums of simple components, facilitate the classification of vibrations in molecules and the study of angular momentum in quantum mechanics through their decomposable representations. The distinction between simple and semisimple frameworks underpins the development of gauge theories and the analysis of invariant subspaces in both pure and applied mathematical contexts.
Common Misconceptions
Simple algebras are often mistakenly thought to be the same as semisimple algebras, but simple algebras contain no nontrivial two-sided ideals, while semisimple algebras are direct sums of simple algebras, allowing for a more complex structure. Another common misconception is that all semisimple algebras must be simple, overlooking that semisimplicity emphasizes decomposability into simple components rather than indivisibility. Understanding that simplicity implies semisimplicity but not vice versa clarifies their distinct algebraic classifications and properties.
Summary and Concluding Thoughts
Simple algebras contain no nontrivial two-sided ideals, making them irreducibly structured and fundamental in representation theory. Semisimple algebras decompose into direct sums of simple algebras, allowing comprehensive classification and enabling modular analysis. Understanding the difference between simple and semisimple structures is crucial for applications in ring theory, module theory, and algebraic geometry.
Simple Infographic
 libterm.com
libterm.com