The canonical module is a fundamental concept in commutative algebra and algebraic geometry, often used to study properties of rings and modules through duality theory. It provides a way to understand the depth, dimension, and structural behavior of Cohen-Macaulay rings by serving as a dualizing module. Explore the rest of this article to uncover how the canonical module influences your algebraic understanding and applications.
Table of Comparison
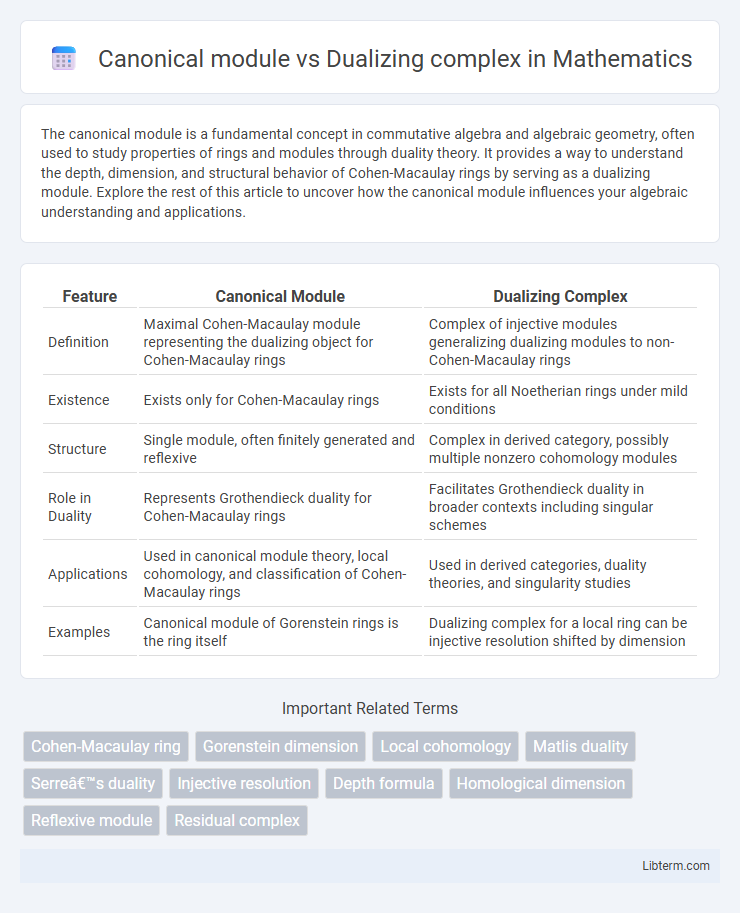
| Feature | Canonical Module | Dualizing Complex |
|---|---|---|
| Definition | Maximal Cohen-Macaulay module representing the dualizing object for Cohen-Macaulay rings | Complex of injective modules generalizing dualizing modules to non-Cohen-Macaulay rings |
| Existence | Exists only for Cohen-Macaulay rings | Exists for all Noetherian rings under mild conditions |
| Structure | Single module, often finitely generated and reflexive | Complex in derived category, possibly multiple nonzero cohomology modules |
| Role in Duality | Represents Grothendieck duality for Cohen-Macaulay rings | Facilitates Grothendieck duality in broader contexts including singular schemes |
| Applications | Used in canonical module theory, local cohomology, and classification of Cohen-Macaulay rings | Used in derived categories, duality theories, and singularity studies |
| Examples | Canonical module of Gorenstein rings is the ring itself | Dualizing complex for a local ring can be injective resolution shifted by dimension |
Introduction to Canonical Module and Dualizing Complex
Canonical modules provide a refined tool in commutative algebra for understanding the intrinsic duality properties of Cohen-Macaulay rings, serving as a key object in local duality theory. Dualizing complexes generalize this concept to a broader class of rings, including non-Cohen-Macaulay cases, by offering a complex in the derived category that facilitates Grothendieck duality. Both concepts are central to homological methods, with canonical modules representing a module-level dualizing object while dualizing complexes encode deeper cohomological duality structures.
Historical Background and Motivation
The concept of the canonical module emerged in commutative algebra as a tool to describe duality properties in Cohen-Macaulay rings, providing a module that behaves like a dualizing object in a more tractable form. Grothendieck introduced the dualizing complex in the 1960s during the development of local cohomology and duality theories, generalizing the notion of dualizing modules to broader classes of rings and schemes, addressing the limitations of canonical modules for non-Cohen-Macaulay contexts. The motivation for both concepts centers on establishing a coherent framework for duality, with the dualizing complex offering a more flexible and powerful apparatus for homological and geometric applications beyond the classical scope of canonical modules.
Definitions and Basic Concepts
The canonical module is a finitely generated module that generalizes the concept of differential forms for Cohen-Macaulay rings, providing a dualizing object in the module category. The dualizing complex is a bounded complex of injective modules that serves as a fundamental tool in Grothendieck duality theory, encoding deep homological information about a ring or scheme. Both notions enable duality principles in commutative algebra and algebraic geometry, but the canonical module is a module-level construct often defined for Cohen-Macaulay rings, whereas the dualizing complex applies in greater generality and captures more refined derived category data.
Canonical Module: Properties and Examples
Canonical modules are finitely generated modules over a Cohen-Macaulay ring that generalize the concept of dualizing modules, providing a framework for duality theory in commutative algebra. Key properties include their uniqueness up to isomorphism, the support matching the ring's dimension, and their role in characterizing Gorenstein rings where the canonical module is isomorphic to the ring itself. Examples of canonical modules appear in local rings of algebraic varieties, where they serve as dualizing objects facilitating local duality theorems and linking homological dimensions with geometric properties.
Dualizing Complex: Properties and Examples
The dualizing complex in algebraic geometry and commutative algebra generalizes the concept of a canonical module, providing a fundamental tool for Grothendieck duality theory. It is a bounded complex of injective modules that reflects key properties such as finite injective dimension, local duality, and supports functorial isomorphisms between Hom and Ext groups. Classic examples include the dualizing complex for a Gorenstein ring, where it is isomorphic to a shift of the canonical module, revealing deep connections between homological dimensions and ring symmetry.
Key Differences Between Canonical Module and Dualizing Complex
The canonical module is a specific type of module over a Noetherian ring exhibiting properties that generalize dualizing sheaves in algebraic geometry, typically used to study Cohen-Macaulay rings and local cohomology. In contrast, the dualizing complex is a bounded complex in the derived category that provides a more flexible and broad framework for Grothendieck duality, applicable to a wider class of schemes or rings. Key differences include the canonical module being a single module often requiring Cohen-Macaulay conditions, whereas the dualizing complex can exist in more general settings and encodes duality through its entire complex structure rather than a single module.
Relationship and Interplay in Commutative Algebra
The canonical module and the dualizing complex both serve as fundamental tools in commutative algebra for studying local cohomology and homological properties of rings, especially Cohen-Macaulay and Gorenstein rings. The canonical module can be viewed as a specific case or "shadow" of the dualizing complex, particularly significant in rings of finite injective dimension, where the dualizing complex generalizes canonical duality to complexes rather than modules. Their interplay allows for powerful duality theorems and facilitates deeper insights into ring structure, depth, and dimension theory, highlighting the intrinsic relationship between homological algebra and algebraic geometry.
Applications in Algebraic Geometry and Homological Algebra
The canonical module provides a concrete tool for studying Cohen-Macaulay rings and their local cohomology, enabling explicit calculations in singularity theory and duality principles. The dualizing complex extends this framework to more general schemes and non-Cohen-Macaulay settings, facilitating Grothendieck duality and derived category formulations in algebraic geometry. Both concepts are fundamental in homological algebra for understanding depth, injective dimensions, and the structure of local cohomology modules.
Criteria for Existence and Construction Methods
The canonical module exists for Cohen-Macaulay rings and can be constructed explicitly using the top local cohomology module or through certain Ext functors relative to a Gorenstein ring. In contrast, the dualizing complex exists more generally for excellent schemes or local rings and is constructed via Grothendieck's duality theory, often involving derived categories and injective resolutions. Criteria for the existence of a dualizing complex are broader, requiring conditions such as finite Krull dimension and noetherian properties, while the canonical module demands stronger assumptions like Cohen-Macaulayness and often a local or graded ring structure.
Summary and Future Directions
The canonical module serves as a key object in commutative algebra, encapsulating duality properties for Cohen-Macaulay rings, while the dualizing complex generalizes this concept to broader classes of rings and schemes, allowing for more flexible duality theories. Research continues to explore extending dualizing complexes to non-Noetherian and singular settings, improving computational methods, and applying these tools in algebraic geometry and representation theory. Future directions emphasize deeper connections with derived categories, enhancing explicit constructions, and integrating with homological conjectures to broaden theoretical and practical impacts.
Canonical module Infographic
 libterm.com
libterm.com