A surjection is a type of function where every element in the target set is mapped to by at least one element from the domain, ensuring full coverage. This concept is essential in mathematical fields such as set theory and algebra for understanding function behaviors. Explore the rest of the article to deepen your grasp of surjections and their applications.
Table of Comparison
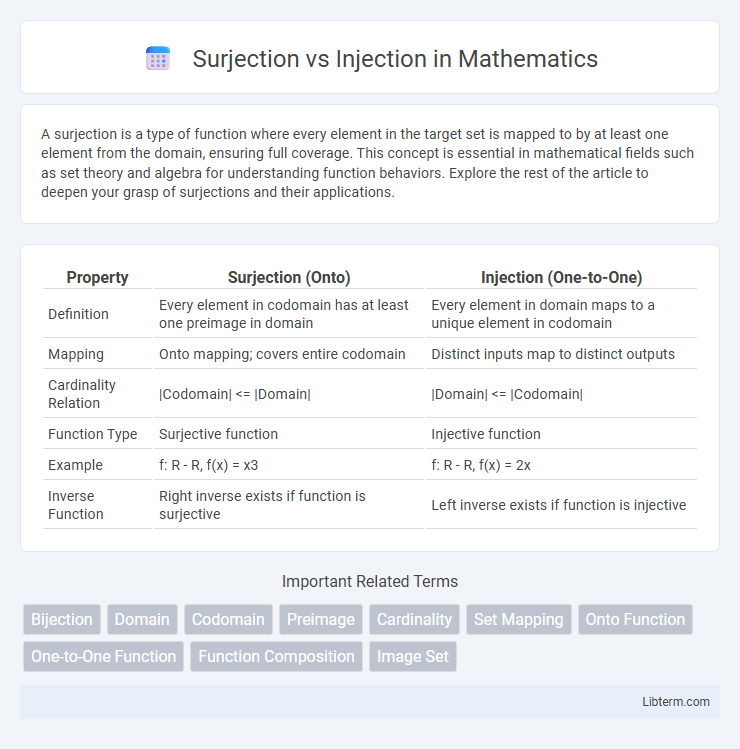
| Property | Surjection (Onto) | Injection (One-to-One) |
|---|---|---|
| Definition | Every element in codomain has at least one preimage in domain | Every element in domain maps to a unique element in codomain |
| Mapping | Onto mapping; covers entire codomain | Distinct inputs map to distinct outputs |
| Cardinality Relation | |Codomain| <= |Domain| | |Domain| <= |Codomain| |
| Function Type | Surjective function | Injective function |
| Example | f: R - R, f(x) = x3 | f: R - R, f(x) = 2x |
| Inverse Function | Right inverse exists if function is surjective | Left inverse exists if function is injective |
Introduction to Functions in Mathematics
Surjection and injection are fundamental concepts in the introduction to functions in mathematics, defining how elements map between sets. A surjection (or onto function) ensures every element in the codomain has a preimage in the domain, emphasizing complete coverage. Injection (or one-to-one function) guarantees distinct elements in the domain map to distinct elements in the codomain, focusing on uniqueness.
Understanding Surjective (Onto) Functions
Surjective (onto) functions map every element of the codomain to at least one element in the domain, ensuring complete coverage of the codomain set. In contrast to injective functions, surjections allow multiple domain elements to correspond to the same codomain element, emphasizing the importance of surjectivity in defining function output range comprehensively. Understanding surjective functions is crucial for analyzing mappings where every possible output is guaranteed representation in the function's range.
Understanding Injective (One-to-One) Functions
Injective functions, also known as one-to-one functions, map each element of the domain to a unique element in the codomain, ensuring no two distinct inputs have the same output. This property is crucial in mathematics and computer science for preserving distinctness and enabling invertibility on the image of the function. Understanding injectivity aids in concepts such as inverses, function composition, and bijections, which are fundamental in set theory and algebra.
Key Differences Between Surjection and Injection
Surjection, also known as onto function, maps every element in the codomain to at least one element in the domain, ensuring full coverage of the target set. Injection, or one-to-one function, assigns distinct elements in the domain to unique elements in the codomain, preventing any duplication of images. The key difference lies in surjection's focus on covering the entire codomain, while injection emphasizes uniqueness and non-repetition of mapping values.
Visualizing Surjection and Injection with Examples
Surjection, or onto function, maps every element of the codomain to at least one element from the domain, illustrated by a function f: R - R where f(x) = x2 + 1 covering all values y >= 1 in the codomain. Injection, or one-to-one function, assigns distinct elements in the domain to distinct elements in the codomain, exemplified by f: R - R where f(x) = 2x, ensuring no two domain points share the same output value. Visualizing these concepts often involves graphing functions to highlight whether every codomain point has a preimage (surjection) or whether each input maps uniquely without duplication in outputs (injection).
Mathematical Definitions and Notations
Surjection, or onto function, is defined as a mapping \( f: A \to B \) where for every element \( b \in B \), there exists at least one \( a \in A \) such that \( f(a) = b \), ensuring the codomain \( B \) is fully covered. Injection, or one-to-one function, requires that if \( f(a_1) = f(a_2) \), then \( a_1 = a_2 \) for all \( a_1, a_2 \in A \), guaranteeing distinct inputs map to distinct outputs. These definitions are formally expressed as: surjection \( \forall b \in B, \exists a \in A : f(a) = b \); injection \( \forall a_1, a_2 \in A, f(a_1) = f(a_2) \implies a_1 = a_2 \).
Real-World Applications of Surjections and Injections
Surjections are crucial in database management systems where every element in a target set, such as user IDs, must correspond to at least one element in the source set, ensuring comprehensive data retrieval. Injections find applications in cryptography, where unique mappings from plaintext to ciphertext prevent collisions and enhance data security. Both concepts underpin algorithms in machine learning for feature mapping and dimensionality reduction, optimizing data representation without loss of essential information.
Importance in Set Theory and Mapping
Surjection and injection are fundamental concepts in set theory that describe specific types of functions crucial for understanding mappings between sets. Surjections ensure that every element in the codomain has a preimage, facilitating the study of onto mappings and enabling the characterization of quotient sets. Injections, characterized by one-to-one mappings, are essential for establishing subset relations and constructing bijections, which form the basis for set equivalence and cardinality comparisons.
Common Mistakes and Misconceptions
A common mistake in understanding surjections and injections is confusing their definitions: injections require each element of the domain to map to a unique element in the codomain, while surjections require every element of the codomain to be mapped by at least one element from the domain. Misconceptions often arise when learners assume that all functions must be both injective and surjective, neglecting the distinct criteria that define one-to-one (injective) and onto (surjective) mappings. Another frequent error is overlooking that a function can be surjective without being injective, and vice versa, which affects properties like invertibility and cardinality relations in set theory.
Surjection, Injection, and Bijection: A Comparative Overview
Surjection, or onto function, maps every element in the codomain to at least one element in the domain, ensuring full coverage of the codomain. Injection, or one-to-one function, assigns distinct elements in the domain to distinct elements in the codomain, preserving uniqueness but not requiring complete codomain coverage. Bijection combines both properties, establishing a perfect pairing between domain and codomain elements, enabling invertible mappings and forming the foundation for equivalence relations in set theory.
Surjection Infographic
 libterm.com
libterm.com