A Taylor series is a powerful mathematical tool that represents functions as infinite sums of terms calculated from the function's derivatives at a single point. This series enables precise approximations of complex functions, making it essential in fields such as calculus, physics, and engineering. Discover how mastering Taylor series can enhance your problem-solving skills by reading the rest of the article.
Table of Comparison
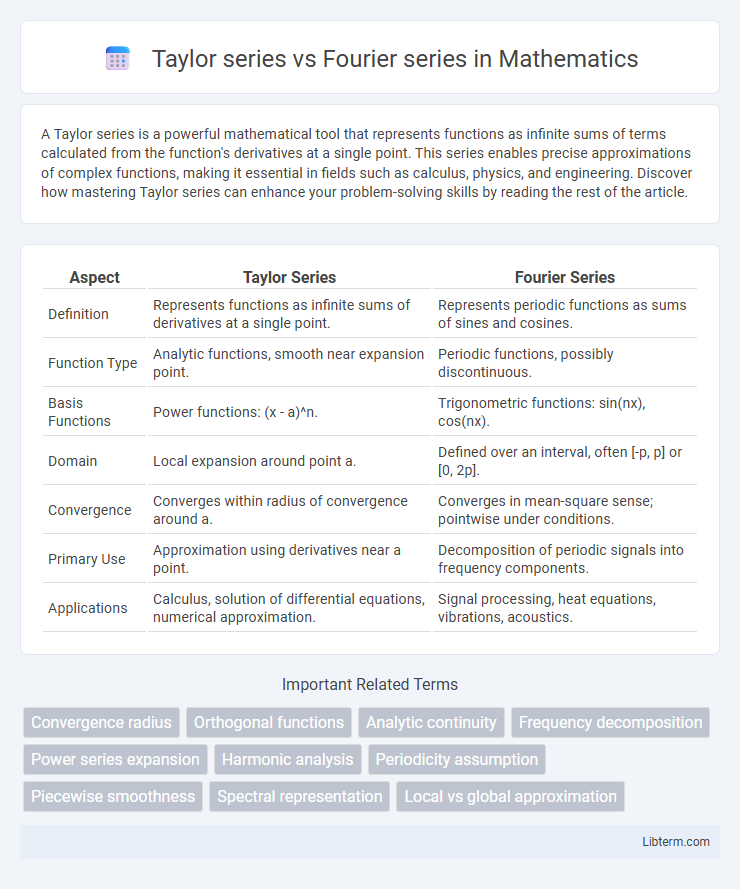
| Aspect | Taylor Series | Fourier Series |
|---|---|---|
| Definition | Represents functions as infinite sums of derivatives at a single point. | Represents periodic functions as sums of sines and cosines. |
| Function Type | Analytic functions, smooth near expansion point. | Periodic functions, possibly discontinuous. |
| Basis Functions | Power functions: (x - a)^n. | Trigonometric functions: sin(nx), cos(nx). |
| Domain | Local expansion around point a. | Defined over an interval, often [-p, p] or [0, 2p]. |
| Convergence | Converges within radius of convergence around a. | Converges in mean-square sense; pointwise under conditions. |
| Primary Use | Approximation using derivatives near a point. | Decomposition of periodic signals into frequency components. |
| Applications | Calculus, solution of differential equations, numerical approximation. | Signal processing, heat equations, vibrations, acoustics. |
Introduction to Taylor and Fourier Series
Taylor series approximate smooth functions using an infinite sum of polynomial terms derived from the function's derivatives at a single point, enabling local function representation and differentiation. Fourier series decompose periodic functions into sums of sine and cosine terms with different frequencies, effectively capturing global behavior through harmonic components. Both series facilitate function analysis, with Taylor series excelling in local approximations and Fourier series in periodic signal processing.
Fundamental Concepts and Definitions
Taylor series approximate functions using infinite sums of derivatives at a single point, representing local behavior with polynomials. Fourier series decompose periodic functions into sums of sines and cosines, capturing global frequency components over an interval. Both serve as powerful tools in mathematical analysis but differ fundamentally in their basis functions and application domains.
Mathematical Formulations
Taylor series express a function as an infinite sum of its derivatives at a single point, formulated as f(x) = S (f(n)(a)/n!)(x - a)n for n=0 to , emphasizing local approximation with power series. Fourier series decompose periodic functions into sums of sines and cosines, represented as f(x) = a0/2 + S [a_n cos(nox) + b_n sin(nox)] for n=1 to , capturing global frequency components. Taylor series focus on smoothness and differentiability at a point, whereas Fourier series leverage orthogonality of trigonometric bases to analyze periodicity in function behavior.
Key Differences Between Taylor and Fourier Series
Taylor series approximates functions using polynomials based on derivatives at a single point, making it ideal for smooth functions near that point, while Fourier series represents functions as sums of sines and cosines, suitable for periodic functions over an interval. Taylor series expansion relies on local behavior and convergence radius, whereas Fourier series captures global frequency components and converges in the mean-square sense. Key differences include the nature of basis functions--polynomial versus trigonometric--and application scope, with Taylor series emphasizing local approximation and Fourier series enabling global periodic analysis.
Domains of Convergence and Applicability
Taylor series converge within a radius determined by the nearest singularity in the complex plane, making them ideal for approximating analytic functions locally around a single point. Fourier series converge in the mean square sense for piecewise continuous periodic functions, allowing representation over entire intervals regardless of pointwise continuity. The Taylor series is suited for local approximations with smooth behavior, whereas Fourier series excel in representing periodic functions with potential discontinuities across their domain.
Use Cases in Science and Engineering
Taylor series excel in approximating smooth, differentiable functions near a specific point, making them invaluable for solving differential equations and modeling physical phenomena like fluid dynamics and electrical circuits. Fourier series decompose periodic signals into sums of sines and cosines, enabling analysis and synthesis of waveforms in signal processing, acoustics, and heat transfer. In engineering, Fourier series optimize system frequency responses, while Taylor series facilitate local behavior approximations and control system designs.
Advantages and Limitations
Taylor series excel at approximating smooth functions locally around a specific point using polynomial terms, providing rapid convergence for analytic functions with well-behaved derivatives. Fourier series effectively decompose periodic functions into sums of sines and cosines, making them ideal for studying signals and systems in frequency domains, especially with applications in heat transfer and vibration analysis. Limitations include Taylor series struggling with non-analytic or discontinuous functions due to poor global convergence, while Fourier series require periodicity and may exhibit Gibbs phenomenon near discontinuities, affecting accuracy.
Illustration with Practical Examples
Taylor series approximate functions locally by expanding them into infinite sums of derivatives at a single point, ideal for smooth, analytic functions, such as sin(x) near zero, where it converges rapidly with polynomials. Fourier series decompose periodic functions into sums of sines and cosines over entire intervals, useful for analyzing signals like square waves in electrical engineering, capturing fundamental frequency and harmonics. Practical application in signal processing shows Taylor series excels in local behavior modeling, while Fourier series is superior for global periodic pattern representation.
Computational Complexity and Efficiency
Taylor series approximate functions using polynomials derived from derivatives at a single point, leading to fast evaluation with complexity primarily dependent on the polynomial degree. Fourier series represent functions as sums of sine and cosine terms, requiring computation of coefficients via integrals, often evaluated using the Fast Fourier Transform (FFT) algorithm with O(n log n) complexity. In terms of efficiency, Taylor series excel in local approximations with low computational cost, while Fourier series provide efficient global approximations for periodic functions, especially when leveraging FFT.
Choosing the Right Series for Your Problem
Choosing between Taylor and Fourier series depends on the problem's nature; Taylor series excel in approximating smooth, analytic functions locally near a point, capturing behavior via polynomial terms derived from derivatives. Fourier series are ideal for periodic functions, decomposing them into sums of sines and cosines to analyze frequency components globally over an interval. For problems involving signal processing or periodic boundary conditions, Fourier series provide superior convergence, while Taylor series suit non-periodic functions requiring local approximation.
Taylor series Infographic
 libterm.com
libterm.com