A locally cartesian closed category provides a rich framework for interpreting dependent types and higher-order logic in category theory, offering powerful tools for structuring mathematical and computational concepts. Its properties enable elegant manipulations of fibered categories and support advanced constructions in homotopy theory and type theory. Explore the rest of the article to deepen your understanding of how these categories can enhance your work in mathematics and computer science.
Table of Comparison
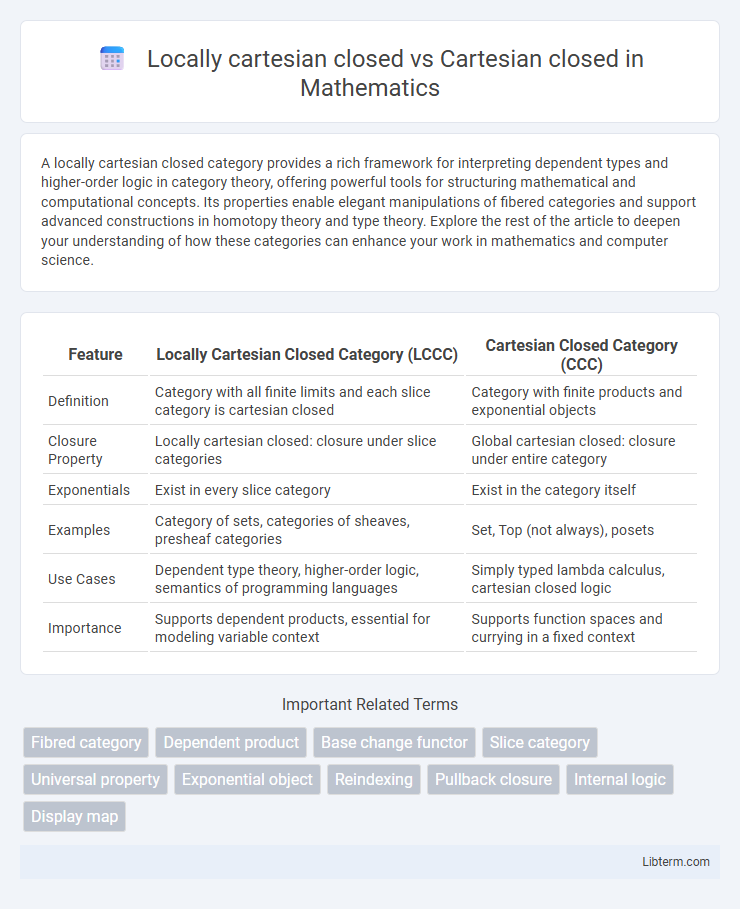
| Feature | Locally Cartesian Closed Category (LCCC) | Cartesian Closed Category (CCC) |
|---|---|---|
| Definition | Category with all finite limits and each slice category is cartesian closed | Category with finite products and exponential objects |
| Closure Property | Locally cartesian closed: closure under slice categories | Global cartesian closed: closure under entire category |
| Exponentials | Exist in every slice category | Exist in the category itself |
| Examples | Category of sets, categories of sheaves, presheaf categories | Set, Top (not always), posets |
| Use Cases | Dependent type theory, higher-order logic, semantics of programming languages | Simply typed lambda calculus, cartesian closed logic |
| Importance | Supports dependent products, essential for modeling variable context | Supports function spaces and currying in a fixed context |
Introduction to Cartesian Closed Categories
Cartesian closed categories (CCCs) provide a framework where objects have internal hom-objects, enabling function spaces and lambda calculus interpretations within category theory. Locally cartesian closed categories (LCCCs) generalize CCCs by requiring that each slice category over an object is itself cartesian closed, allowing more refined handling of dependent types and indexed families. This structure is fundamental in categorical logic and type theory, bridging categorical semantics with dependent type systems.
Understanding Locally Cartesian Closed Categories
Locally cartesian closed categories (LCCCs) generalize cartesian closed categories (CCCs) by requiring that every slice category be cartesian closed, enabling the interpretation of dependent types and higher-order logic within each fiber. Unlike CCCs, which only guarantee exponentials globally, LCCCs support more refined constructions such as pullbacks and internal hom-objects varying over different base objects, facilitating a richer categorical semantics for dependent type theories. This structure is fundamental in understanding categorical models of type theory and sheaf theory, where local cartesian closure captures context-dependent function spaces and variable binding mechanisms.
Key Differences Between CCC and LCCC
Cartesian closed categories (CCC) provide a framework where every object has a corresponding exponential object, ensuring the existence of function spaces and supporting simply typed lambda calculus. Locally cartesian closed categories (LCCC) extend this by requiring each slice category to be cartesian closed, enabling dependent types and more expressive internal logic for modeling variable contexts. Key differences include LCCCs' ability to handle dependent products and sums, making them fundamental in higher-order type theory, unlike CCCs which are limited to non-dependent function spaces.
Examples of Cartesian Closed Categories
Cartesian closed categories include Set, the category of sets and functions, and Poset, the category of partially ordered sets with monotone functions. Top, the category of topological spaces and continuous maps, is not cartesian closed, but its subcategory of compactly generated spaces is. In contrast, locally cartesian closed categories generalize cartesian closedness by requiring the slice categories over any object to be cartesian closed, as seen in categories like the category of sheaves on a site.
Examples of Locally Cartesian Closed Categories
Locally cartesian closed categories (LCCCs) extend cartesian closed categories (CCCs) by requiring the existence of right adjoints to pullback functors, enabling dependent type constructions. Common examples of LCCCs include the category of sets (Set), the category of presheaves on a small category, and the category of sheaves on a site, which support dependent sums and products critical for modeling type theory. In contrast, Cartesian closed categories like Set focus solely on product and exponential objects without the additional structure required for dependent types.
Functorial Properties in CCC vs LCCC
Cartesian closed categories (CCCs) exhibit functorial properties where exponential objects correspond to internal hom-functors, enabling well-defined currying and evaluation maps consistent across the category. Locally cartesian closed categories (LCCCs) extend this structure by ensuring each slice category is cartesian closed, allowing for dependent types and fibrations to be handled functorially via pullback functors that preserve these exponential objects. This local cartesian closure enriches the functorial behavior by incorporating context-dependent transformations, crucial for modeling dependent type theory and categorical logic.
Internal Logic: Lambda Calculus & Dependent Types
Locally cartesian closed categories (LCCCs) extend Cartesian closed categories (CCCs) by supporting dependent types essential for modeling dependent lambda calculus and internal logic with variable contexts. While CCCs facilitate standard simply typed lambda calculus through their exponential objects, LCCCs capture a richer internal language enabling both dependent function types (P-types) and dependent pair types (S-types). This structure allows LCCCs to interpret powerful type theories like Martin-Lof type theory, enhancing the expressiveness of internal logic beyond the scope of CCCs.
Applications in Category Theory and Computer Science
Locally cartesian closed categories generalize cartesian closed categories by supporting dependent types and interpreting contexts with variable dependencies, crucial for modeling type theories in computer science. Cartesian closed categories are fundamental in representing simply-typed lambda calculus, enabling function spaces and application-based reasoning in programming language semantics. The richer structure of locally cartesian closed categories facilitates advanced applications such as dependent type theories, higher-order abstract syntax, and the categorical semantics of proof assistants.
Why Choose Locally Cartesian Closed Categories?
Locally cartesian closed categories generalize cartesian closed categories by allowing each slice category to be cartesian closed, enabling more sophisticated handling of dependent types and variable contexts essential in category theory and type theory applications. This property makes locally cartesian closed categories particularly suitable for modeling dependent type theories, homotopy type theory, and sophisticated logical frameworks where context-dependent constructions are pivotal. Their enhanced expressive power compared to cartesian closed categories supports advanced semantics in programming languages, higher-order logic, and formal verification systems.
Summary: CCC vs LCCC in Modern Mathematics
Cartesian closed categories (CCCs) provide a foundational framework for modeling simply typed lambda calculus with products, emphasizing global exponentiation and terminal objects. Locally cartesian closed categories (LCCCs) extend this structure by incorporating slice categories that are themselves cartesian closed, enabling a refined treatment of dependent types and variable contexts central to modern type theory and homotopy type theory. The distinction between CCCs and LCCCs is pivotal in contemporary mathematics, as LCCCs offer a powerful setting for interpreting dependent type theories and higher-order categorical semantics, surpassing the expressive power of traditional CCC frameworks.
Locally cartesian closed Infographic
 libterm.com
libterm.com