A free group is a fundamental concept in abstract algebra, defined by a set of generators with no relations other than those required by group axioms. This structure allows every element to be uniquely represented as a finite sequence of generator symbols and their inverses, enabling simplified group calculations and theoretical analysis. Explore the rest of the article to deepen your understanding of free groups and their applications.
Table of Comparison
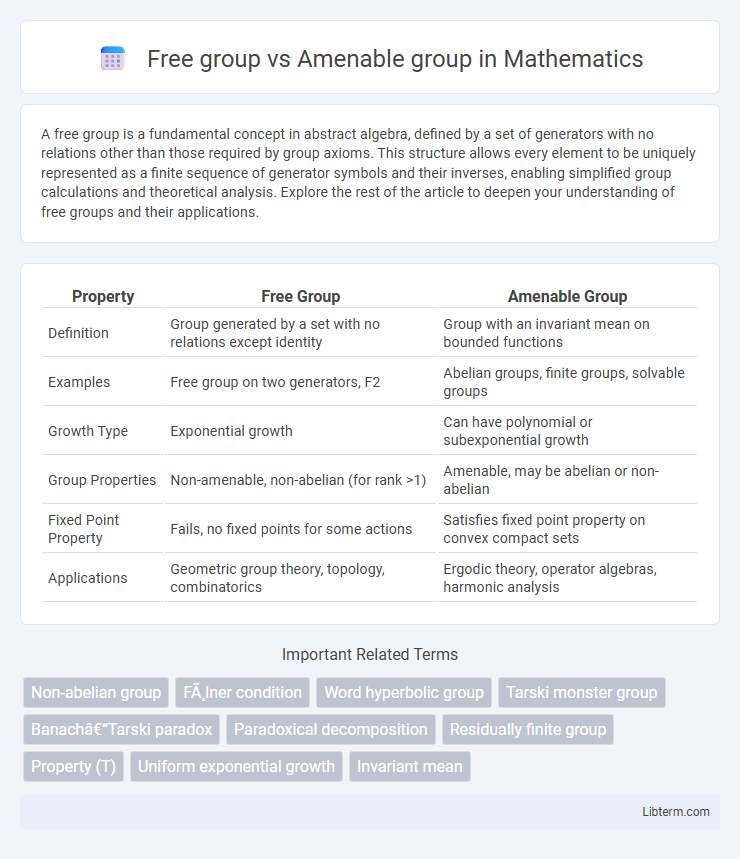
| Property | Free Group | Amenable Group |
|---|---|---|
| Definition | Group generated by a set with no relations except identity | Group with an invariant mean on bounded functions |
| Examples | Free group on two generators, F2 | Abelian groups, finite groups, solvable groups |
| Growth Type | Exponential growth | Can have polynomial or subexponential growth |
| Group Properties | Non-amenable, non-abelian (for rank >1) | Amenable, may be abelian or non-abelian |
| Fixed Point Property | Fails, no fixed points for some actions | Satisfies fixed point property on convex compact sets |
| Applications | Geometric group theory, topology, combinatorics | Ergodic theory, operator algebras, harmonic analysis |
Introduction to Group Theory
Free groups serve as foundational examples in group theory, characterized by a set of generators with no relations other than the group axioms, representing the most unrestricted algebraic structures. Amenable groups include groups that admit an invariant mean, encompassing finite groups, abelian groups, and solvable groups, and are crucial for understanding phenomena in ergodic theory and harmonic analysis. The contrast between free groups, which are non-amenable and exhibit exponential growth, and amenable groups highlights essential differences in algebraic properties and applications within mathematical analysis and topology.
Defining Free Groups
Free groups are algebraic structures generated by a set of elements where no relations exist other than those required by group axioms, allowing for unique reduced word representations. They contrast with amenable groups, which possess an invariant mean and satisfy the Folner condition, highlighting differences in growth, boundary behavior, and measure-theoretic properties. Defining free groups involves specifying a basis set whose elements and their inverses freely generate all group members without imposed relations.
Defining Amenable Groups
Amenable groups are defined by the existence of a finitely additive, left-invariant probability measure on all their subsets, distinguishing them from free groups, which lack such invariant means. This invariant measure property implies that amenable groups satisfy the Folner condition, allowing for approximations by finite subsets with small boundary relative to volume. In contrast, free groups, being non-amenable, exhibit exponential growth and fail to admit invariant means, making them fundamental objects in geometric group theory and ergodic theory.
Historical Development of Free and Amenable Groups
The concept of free groups was introduced by Jakob Nielsen in the 1920s to formalize the idea of groups generated by sets without relations, providing a foundation for combinatorial group theory. Amenable groups emerged in the 1920s through John von Neumann's work addressing the Banach-Tarski paradox, defining groups with invariant means and linking group theory to measure theory. The historical development of free and amenable groups reflects a progression from purely algebraic structures to those intertwining algebra, analysis, and geometric group theory.
Key Properties of Free Groups
Free groups exhibit the property of having a basis consisting of freely generating elements, enabling any element to be uniquely expressed as a reduced word over this basis. They are non-amenable, characterized by exponential growth and containing free subgroups of rank two or more, which contrasts with amenable groups that have invariant means and satisfy Folner conditions. The absence of a finitely additive invariant measure on free groups highlights their key divergence from amenable groups in harmonic analysis and geometric group theory.
Key Properties of Amenable Groups
Amenable groups are characterized by the existence of an invariant mean, which ensures they admit finitely additive measures invariant under group action, distinguishing them from free groups that lack this property. These groups display important properties such as closure under taking subgroups, quotients, and extensions, as well as having fixed-point properties on compact convex sets. Unlike free groups, amenable groups do not contain paradoxical decompositions, reflecting their measure-theoretic and geometric regularity.
Distinctions Between Free and Amenable Groups
Free groups have a structure characterized by non-abelian, highly non-amenable properties with exponential growth and no invariant mean, distinguishing them sharply from amenable groups. Amenable groups possess an invariant mean, exhibit subexponential or polynomial growth, and include all finite, abelian, and solvable groups, reflecting a level of measure-theoretic regularity absent in free groups. These distinctions underpin critical differences in geometric group theory, ergodic theory, and operator algebras, emphasizing the contrasting complexity and symmetry in their algebraic and analytical behaviors.
Examples of Free and Amenable Groups
Free groups include the infinite free group on two or more generators, characterized by all reduced words formed from these generators without any relations except the group axioms. Amenable groups comprise all finite groups, abelian groups like the integers under addition, and solvable groups such as the group of upper triangular matrices with entries in a field. While a free group on two or more generators is non-amenable due to its exponential growth and lack of invariant mean, amenable groups exhibit properties like the existence of Folner sets and invariant means.
Applications in Mathematics and Other Fields
Free groups are fundamental in algebraic topology and geometric group theory, providing a framework for modeling symmetry and group actions with minimal relations, which is crucial in combinatorial group theory and the study of covering spaces. Amenable groups, characterized by the existence of invariant means, have significant applications in ergodic theory, harmonic analysis, and probability theory, contributing to the understanding of dynamical systems, random walks, and operator algebras. The distinctions between free and amenable groups influence the classification of group von Neumann algebras and impact theoretical physics, particularly in statistical mechanics and quantum field theory.
Open Problems and Research Directions
Open problems in the study of free groups versus amenable groups include characterizing the borderlines of amenability within various classes of groups and understanding the implications for group actions on different spaces. Research directions emphasize exploring connections between geometric group theory and operator algebras, particularly examining whether certain group properties imply amenability or non-amenability. Advances in understanding the structure of free groups provide insight into the limits of amenability, guiding investigations into invariant means, growth rates, and ergodic theory applications.
Free group Infographic
 libterm.com
libterm.com