Torsion-free abelian groups are algebraic structures where no element other than the identity has finite order, meaning multiplying any non-identity element by a nonzero integer never results in the identity. These groups play a critical role in module theory and algebraic topology due to their structural properties and lack of torsion elements. Explore the rest of the article to deepen your understanding of torsion-free abelian groups and their applications.
Table of Comparison
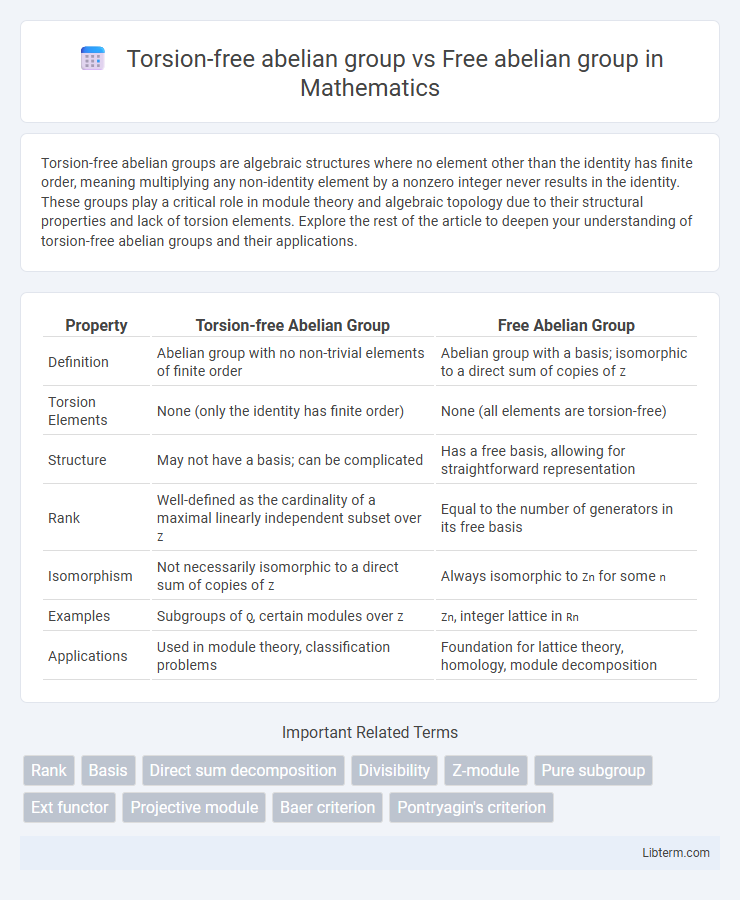
| Property | Torsion-free Abelian Group | Free Abelian Group |
|---|---|---|
| Definition | Abelian group with no non-trivial elements of finite order | Abelian group with a basis; isomorphic to a direct sum of copies of Z |
| Torsion Elements | None (only the identity has finite order) | None (all elements are torsion-free) |
| Structure | May not have a basis; can be complicated | Has a free basis, allowing for straightforward representation |
| Rank | Well-defined as the cardinality of a maximal linearly independent subset over Z |
Equal to the number of generators in its free basis |
| Isomorphism | Not necessarily isomorphic to a direct sum of copies of Z |
Always isomorphic to Zn for some n |
| Examples | Subgroups of Q, certain modules over Z |
Zn, integer lattice in Rn |
| Applications | Used in module theory, classification problems | Foundation for lattice theory, homology, module decomposition |
Introduction to Abelian Groups
Torsion-free abelian groups are abelian groups in which no nonzero element has finite order, ensuring elements cannot be annihilated by multiplication with a nonzero integer. Free abelian groups are a special subclass characterized by a basis, meaning every element can be uniquely expressed as a finite linear combination of basis elements with integer coefficients. Understanding the distinction between torsion-free and free abelian groups is fundamental in the study of abelian groups, as it highlights structural differences critical to classification and application in algebraic topology and module theory.
Defining Free Abelian Groups
Free abelian groups are defined as abelian groups with a basis, allowing every element to be uniquely expressed as a finite linear combination of basis elements with integer coefficients. A torsion-free abelian group has no elements of finite order except the identity, but unlike free abelian groups, it may lack a basis for unique representation. The key distinction lies in the existence of a free generating set in free abelian groups, making them structurally simpler and fully decomposable into direct sums of copies of the integers.
What are Torsion-Free Abelian Groups?
Torsion-free abelian groups are abelian groups in which no nonzero element has finite order, meaning for every nonzero element \( x \) and every nonzero integer \( n \), the equation \( nx = 0 \) does not hold. These groups generalize free abelian groups by allowing more complex structures without elements of finite order, distinguishing them from groups with torsion elements. Unlike free abelian groups, which are isomorphic to direct sums of copies of the integers \( \mathbb{Z} \), torsion-free abelian groups may not have a basis or decomposition into simple integer modules.
Key Differences Between Free and Torsion-Free Abelian Groups
Free abelian groups are characterized by the presence of a basis, allowing every element to be uniquely expressed as a finite linear combination of basis elements with integer coefficients. Torsion-free abelian groups lack elements of finite order other than the identity but do not necessarily admit a basis, which means they may not be free. The fundamental difference lies in the structure: all free abelian groups are torsion-free, but not all torsion-free abelian groups are free, particularly in cases of higher rank or infinite generation.
Examples of Free Abelian Groups
Free abelian groups are abelian groups with a basis such that every element can be uniquely expressed as a finite linear combination of basis elements with integer coefficients, exemplified by the group \(\mathbb{Z}^n\) for some integer \(n\). Torsion-free abelian groups, in contrast, are abelian groups with no nontrivial elements of finite order, but they may lack a free basis, such as the additive group of rational numbers \(\mathbb{Q}\). Classic examples of free abelian groups include \(\mathbb{Z}\), \(\mathbb{Z}^2\), and more generally, \(\mathbb{Z}^n\), each serving as foundational structures in algebra and topology due to their direct sum decomposition and free generators.
Examples of Torsion-Free Non-Free Abelian Groups
Torsion-free abelian groups are groups where no nonzero element has finite order, but not all such groups are free abelian groups, which are direct sums of infinite cyclic groups. A classic example of torsion-free non-free abelian groups is the additive group of rational numbers \(\mathbb{Q}\), which is torsion-free but not free since it cannot be decomposed into a direct sum of copies of \(\mathbb{Z}\). Other examples include nontrivial subgroups of \(\mathbb{Q}^n\) that fail to have a basis over \(\mathbb{Z}\), illustrating the distinction between torsion-free and free abelian groups.
Structure Theorem for Finitely Generated Abelian Groups
Torsion-free abelian groups are characterized by the absence of elements with finite order except the identity, whereas free abelian groups have a basis allowing every element to be uniquely expressed as an integer linear combination of basis elements. The Structure Theorem for Finitely Generated Abelian Groups states that every finitely generated abelian group is isomorphic to a direct sum of a free abelian group of finite rank and a finite torsion subgroup. This decomposition highlights that finitely generated torsion-free abelian groups are precisely free abelian groups, confirming their classification via rank and basis elements.
Applications of Torsion-Free and Free Abelian Groups
Torsion-free abelian groups play a crucial role in algebraic topology and module theory, where their structure aids in understanding homology groups and linear independence over integral domains. Free abelian groups find extensive applications in combinatorial group theory and algebraic K-theory, providing foundational models for groups with well-defined bases facilitating computations of invariants. Both structures are pivotal in number theory and cryptographic algorithms, with torsion-free groups ensuring stability in group actions and free abelian groups offering a basis for analyzing lattice structures.
Criteria for Identifying Free Abelian Groups
A free abelian group is characterized by the existence of a basis such that every element can be uniquely expressed as a finite linear combination of basis elements with integer coefficients, whereas torsion-free abelian groups have no elements of finite order but do not necessarily possess such a basis. The criterion for identifying a free abelian group involves verifying the presence of a generating set that is linearly independent over the integers, ensuring its structure is isomorphic to a direct sum of copies of the integer group Z. In contrast, torsion-free abelian groups may lack this linear independence property, making free abelian groups a strict subset distinguished by their basis and decomposability into free components.
Summary: Comparing Free and Torsion-Free Abelian Groups
Free abelian groups are characterized by a basis allowing every element to be expressed uniquely as an integer linear combination of basis elements, ensuring a completely decomposable and direct sum structure. Torsion-free abelian groups, while containing no elements of finite order other than the identity, may lack a basis and cannot always be decomposed into a direct sum of infinite cyclic groups. The key distinction lies in that all free abelian groups are torsion-free, but not all torsion-free abelian groups are free, reflecting differences in structural and decomposability properties.
Torsion-free abelian group Infographic
 libterm.com
libterm.com