Graded algebra is a powerful mathematical framework where algebraic structures are decomposed into direct sums indexed by degrees, enabling the study of elements based on their grading properties. This approach is essential in areas like homological algebra, algebraic topology, and representation theory, providing tools to analyze complex systems with hierarchical layers. Explore the rest of the article to deepen your understanding of graded algebra's versatile applications and foundational concepts.
Table of Comparison
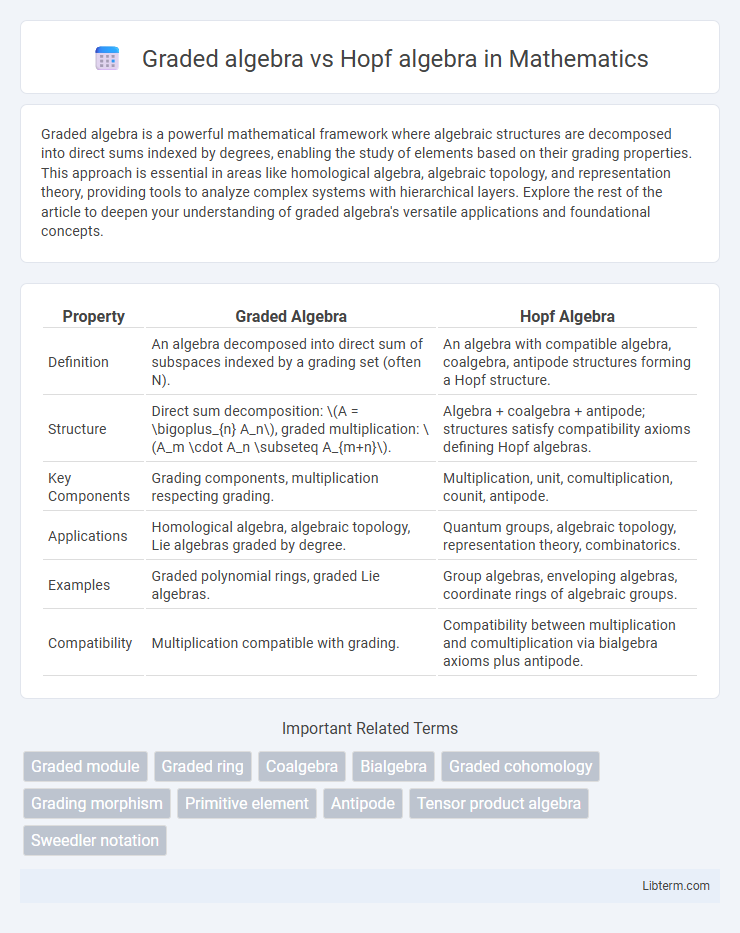
| Property | Graded Algebra | Hopf Algebra |
|---|---|---|
| Definition | An algebra decomposed into direct sum of subspaces indexed by a grading set (often N). | An algebra with compatible algebra, coalgebra, antipode structures forming a Hopf structure. |
| Structure | Direct sum decomposition: \(A = \bigoplus_{n} A_n\), graded multiplication: \(A_m \cdot A_n \subseteq A_{m+n}\). | Algebra + coalgebra + antipode; structures satisfy compatibility axioms defining Hopf algebras. |
| Key Components | Grading components, multiplication respecting grading. | Multiplication, unit, comultiplication, counit, antipode. |
| Applications | Homological algebra, algebraic topology, Lie algebras graded by degree. | Quantum groups, algebraic topology, representation theory, combinatorics. |
| Examples | Graded polynomial rings, graded Lie algebras. | Group algebras, enveloping algebras, coordinate rings of algebraic groups. |
| Compatibility | Multiplication compatible with grading. | Compatibility between multiplication and comultiplication via bialgebra axioms plus antipode. |
Introduction to Graded Algebras
Graded algebras are algebraic structures decomposed into direct sums of subspaces indexed by a grading set, often the non-negative integers, which allows for degree-wise operations central to homological algebra and algebraic topology. Unlike Hopf algebras, graded algebras emphasize the hierarchical layering of elements by degree, facilitating the study of algebraic objects with intrinsic gradation properties, such as polynomial rings and cohomology rings. This degree-based framework underpins advanced constructions in representation theory and category theory, providing a foundational tool distinct from the bialgebraic intertwining of multiplication and comultiplication seen in Hopf algebras.
Fundamental Structure of Hopf Algebras
Hopf algebras extend graded algebras by incorporating a rich structure combining algebra and coalgebra properties equipped with an antipode map, enabling dual operations such as convolution and symmetry in algebraic topology and quantum groups. The fundamental structure of Hopf algebras includes a multiplication, unit, comultiplication, counit, and antipode that satisfy compatibility axioms ensuring coherence between these maps. This algebraic framework supports graded structures but enhances them with coalgebraic duality and invertibility features critical for applications in representation theory and non-commutative geometry.
Key Differences Between Graded and Hopf Algebras
Graded algebras consist of direct sum decompositions indexed by integers or other grading sets, allowing elements to be studied according to their degree, while Hopf algebras combine algebra, coalgebra, and antipode structures to facilitate duality and symmetry operations in algebraic topology and quantum groups. The key difference lies in the presence of a compatible coalgebra structure and antipode in Hopf algebras, which is absent in graded algebras that primarily emphasize degree-based composition. Applications of Hopf algebras include representation theory and quantum field theory, contrasting with graded algebras' role in homological algebra and graded ring theory.
Algebraic Operations: Grading vs. Coalgebra Structure
Graded algebras feature a decomposition into direct sums indexed by a grading set, where multiplication respects the grading by combining elements from graded components to produce outputs in a corresponding grade. Hopf algebras incorporate both algebraic and coalgebraic structures, equipped with multiplication, unit, comultiplication, counit, and antipode maps, satisfying compatibility conditions that unify algebra and coalgebra properties. The key distinction lies in graded algebras focusing on the stratification of elements via grading, while Hopf algebras emphasize dual algebraic and coalgebraic operations facilitating structures like group-like and primitive elements.
Examples of Graded Algebras
Examples of graded algebras include polynomial rings with natural degree gradation, exterior algebras with degree given by wedge product length, and group algebras graded by group elements. Unlike Hopf algebras, graded algebras emphasize decomposition into homogeneous components without necessarily having comultiplication or antipode structures. Common examples of Hopf algebras arise in quantum groups and algebraic topology, where grading assists in cohomological computations but the structures extend beyond simple grading.
Classic Illustrations of Hopf Algebras
Classic illustrations of Hopf algebras include group algebras and coordinate rings of algebraic groups, which possess rich algebraic structures combining multiplication, comultiplication, and antipode maps. In contrast, graded algebras are vector spaces decomposed into direct sums indexed by grades, emphasizing filtration without necessarily including coproduct or antipode operations. Hopf algebras extend the concept of graded algebras by incorporating coalgebra and antipode properties critical in fields such as quantum groups and algebraic topology.
Compatibility Conditions in Both Algebra Types
Graded algebras require a multiplication operation compatible with the grading, ensuring the product of elements from graded components respects the additive grading structure. Hopf algebras combine algebra and coalgebra structures with compatibility conditions between multiplication, comultiplication, unit, counit, and antipode maps, guaranteeing coherence in their bialgebra and antipodal properties. The key distinction lies in graded algebras enforcing degree compatibility in multiplication, while Hopf algebras demand intricate compatibility between both algebraic and coalgebraic operations.
Applications of Graded and Hopf Algebras
Graded algebras find extensive applications in algebraic topology, particularly in the study of cohomology rings and spectral sequences, where their grading encodes geometric or topological information. Hopf algebras play a crucial role in quantum groups, non-commutative geometry, and the theory of Lie groups, enabling the algebraic formalism of symmetry and duality concepts. Both structures are instrumental in representation theory, with graded algebras often organizing module categories by degree and Hopf algebras providing key frameworks for tensor categories and quantum invariants.
Interconnections: When Graded Algebras Become Hopf Algebras
Graded algebras transform into Hopf algebras when equipped with a compatible coalgebra structure, allowing the grading to align with the coproduct and antipode maps. This interplay ensures that the algebra's gradation respects the Hopf algebra axioms, particularly the coassociativity and counit conditions within each graded component. Examples include graded connected Hopf algebras, where the degree zero part forms the base field, facilitating a rich theory connecting representation theory and quantum groups.
Summary: Choosing Between Graded and Hopf Algebraic Frameworks
Graded algebras provide a structured decomposition by degree, facilitating the analysis of algebraic objects through layers corresponding to grading components, which is crucial in homological algebra and representation theory. Hopf algebras combine algebraic and coalgebraic structures with antipodes, enabling the study of symmetry in algebraic topology, quantum groups, and noncommutative geometry. Choosing between graded and Hopf algebraic frameworks depends on the problem's need for layered structural insights versus the requirement for dual algebra-coalgebra interactions and symmetry operations.
Graded algebra Infographic
 libterm.com
libterm.com