Harmonic frequencies play a crucial role in music and signal processing by enriching sounds and enhancing audio clarity. Understanding how harmonics interact can help you optimize acoustic environments and improve sound quality. Explore the article to dive deeper into the science and applications of harmonics.
Table of Comparison
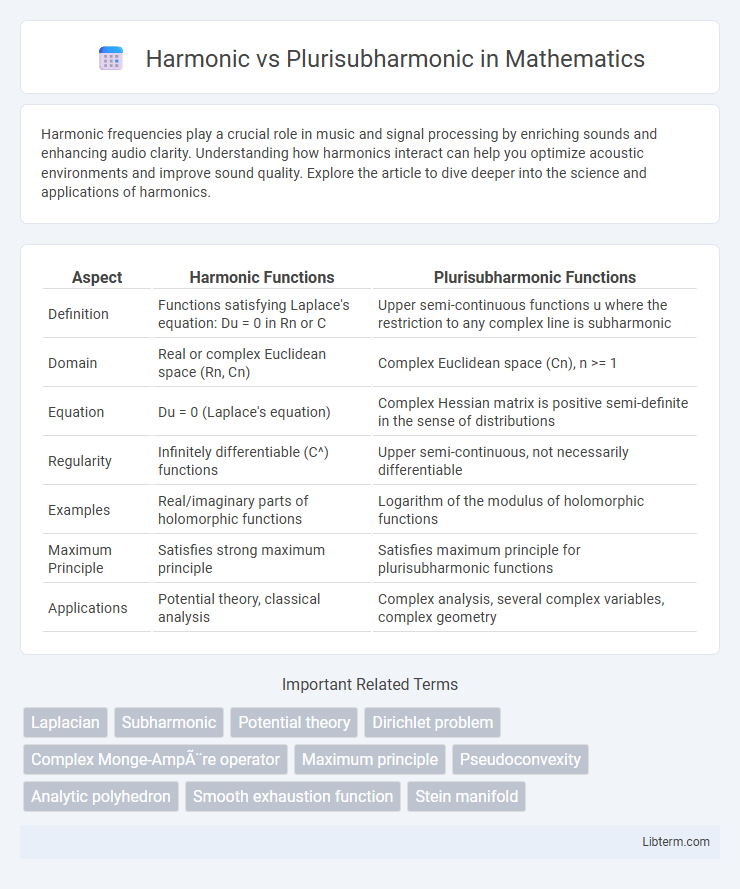
| Aspect | Harmonic Functions | Plurisubharmonic Functions |
|---|---|---|
| Definition | Functions satisfying Laplace's equation: Du = 0 in Rn or C | Upper semi-continuous functions u where the restriction to any complex line is subharmonic |
| Domain | Real or complex Euclidean space (Rn, Cn) | Complex Euclidean space (Cn), n >= 1 |
| Equation | Du = 0 (Laplace's equation) | Complex Hessian matrix is positive semi-definite in the sense of distributions |
| Regularity | Infinitely differentiable (C^) functions | Upper semi-continuous, not necessarily differentiable |
| Examples | Real/imaginary parts of holomorphic functions | Logarithm of the modulus of holomorphic functions |
| Maximum Principle | Satisfies strong maximum principle | Satisfies maximum principle for plurisubharmonic functions |
| Applications | Potential theory, classical analysis | Complex analysis, several complex variables, complex geometry |
Introduction to Harmonic and Plurisubharmonic Functions
Harmonic functions satisfy Laplace's equation, exhibiting mean value properties and arising naturally in potential theory, while plurisubharmonic functions generalize subharmonic functions to several complex variables, characterized by their upper semi-continuity and complex Hessian positivity. Both function classes are fundamental in complex analysis and partial differential equations, with harmonic functions representing equilibrium states and plurisubharmonic functions serving as tools in complex geometry and several complex variables theory. Their interplay enriches the study of complex manifolds and potential theory, defining key regularity and convexity concepts.
Mathematical Definitions and Core Concepts
Harmonic functions are twice continuously differentiable functions satisfying Laplace's equation, u = 0, indicating that they have zero Laplacian and are characterized by mean value properties and smoothness. Plurisubharmonic functions generalize subharmonic functions to several complex variables, requiring upper semi-continuity and the property that their restriction to any complex line is subharmonic, playing a central role in complex analysis and several complex variables. The key distinction lies in harmonic functions being solutions to a linear PDE with precise smoothness, while plurisubharmonic functions form a convex cone of functions that are generally less regular but instrumental in complex potential theory.
Key Differences Between Harmonic and Plurisubharmonic Functions
Harmonic functions are twice continuously differentiable functions that satisfy Laplace's equation, resulting in mean value properties and the condition of being both subharmonic and superharmonic. Plurisubharmonic functions generalize subharmonic functions to several complex variables, characterized by their upper semi-continuity and the property that their restriction to any complex line is subharmonic. The key differences lie in domain and dimensionality: harmonic functions apply to real variables with strict Laplace equations, whereas plurisubharmonic functions operate in complex variables with a focus on complex Hessian positivity conditions.
Properties and Theorems of Harmonic Functions
Harmonic functions, defined as twice continuously differentiable functions satisfying Laplace's equation Du = 0, exhibit the mean value property, ensuring the function's value at any point equals the average over surrounding spheres. Key theorems include the Maximum Principle, stating that harmonic functions achieve their extrema on the boundary of a domain, and the Weyl's Lemma, which guarantees smoothness and analyticity of solutions. In contrast, plurisubharmonic functions generalize subharmonic functions to several complex variables, lacking strict linearity but preserving properties like upper semi-continuity and the comparison principle within complex domains.
Essential Properties of Plurisubharmonic Functions
Plurisubharmonic functions are upper semi-continuous functions defined on complex domains that generalize subharmonic functions to several complex variables, characterized by their property of being subharmonic along every complex line. Essential properties include their stability under taking maximums, closure under limits of decreasing sequences, and the fact that they cannot attain a local maximum unless constant, reflecting their critical role in complex analysis and potential theory. In contrast to harmonic functions, which are smooth solutions to Laplace's equation, plurisubharmonic functions may lack smoothness but still capture complex convexity through their Levi form being positive semi-definite.
Applications in Complex Analysis and Potential Theory
Harmonic functions, characterized by satisfying Laplace's equation, play a central role in classical potential theory and model steady-state heat flow and electrostatics. Plurisubharmonic functions extend the concept of subharmonicity to several complex variables, crucial for complex analysis, particularly in understanding pseudoconvexity and the theory of several complex variables. Applications include solving the Dirichlet problem for harmonic functions, while plurisubharmonic functions underpin the construction of plurisubharmonic exhaustion functions essential in the study of complex manifolds and domains of holomorphy.
Geometric Interpretation and Visualizations
Harmonic functions represent solutions to Laplace's equation, visually characterized by smooth surfaces with no local maxima or minima inside the domain, reflecting equilibrium states such as steady heat distribution. Plurisubharmonic functions generalize subharmonic functions to several complex variables, forming level sets that resemble convex shapes in complex Euclidean space and embody complex geometric structures like pseudoconvexity. Geometrically, harmonic functions illustrate potential theory's equilibrium, while plurisubharmonic functions capture complex analytic geometry's convexity in multidimensional complex domains.
Role in Partial Differential Equations
Harmonic functions satisfy Laplace's equation Du = 0 and play a central role in solving boundary value problems in partial differential equations, representing equilibrium states in physics. Plurisubharmonic functions generalize subharmonic functions to several complex variables, crucial in complex analysis and complex Monge-Ampere equations, providing tools for studying pseudoconvex domains and pluripotential theory. The contrast lies in harmonic functions being solutions to elliptic PDEs, while plurisubharmonic functions serve as upper semicontinuous functions that help characterize complex structures via plurisubharmonicity conditions.
Examples in Real and Complex Spaces
Harmonic functions in real spaces include solutions to Laplace's equation like u(x,y) = x2 - y2, which are twice continuously differentiable with zero Laplacian. Plurisubharmonic functions in complex spaces often appear as upper semi-continuous functions u(z,w) = log|z| or u(z,w) = |z|2 + |w|2, exhibiting subharmonicity along complex lines and playing a crucial role in several complex variables theory. These examples highlight harmonic functions' real-variable PDE nature versus plurisubharmonic functions' complex-variable convexity and analytic structure.
Comparison Table: Harmonic vs Plurisubharmonic Functions
Harmonic functions satisfy Laplace's equation Du = 0 and are real-valued with mean value properties in Euclidean spaces, whereas plurisubharmonic functions are upper semi-continuous, defined on complex variables, and satisfy the complex Hessian inequality 2u/z_jz_k >= 0 in the sense of distributions. Harmonic functions are both subharmonic and superharmonic, ensuring smoothness and analytic continuation, while plurisubharmonic functions generalize subharmonicity to several complex variables with applications in complex analysis and complex geometry. The comparison table highlights distinctions in domain (real vs complex), smoothness (harmonic functions are smooth, plurisubharmonic functions may be non-smooth), and key properties such as mean value property versus pseudoconvexity.
Harmonic Infographic
 libterm.com
libterm.com