Cell complexes provide a structured way to study topological spaces by decomposing them into basic building blocks called cells, such as points, line segments, and disks. This approach helps analyze shapes and spaces in various dimensions, revealing properties like connectivity and holes through homology and homotopy theories. Explore the full article to understand how cell complexes can deepen your grasp of geometric and algebraic topology.
Table of Comparison
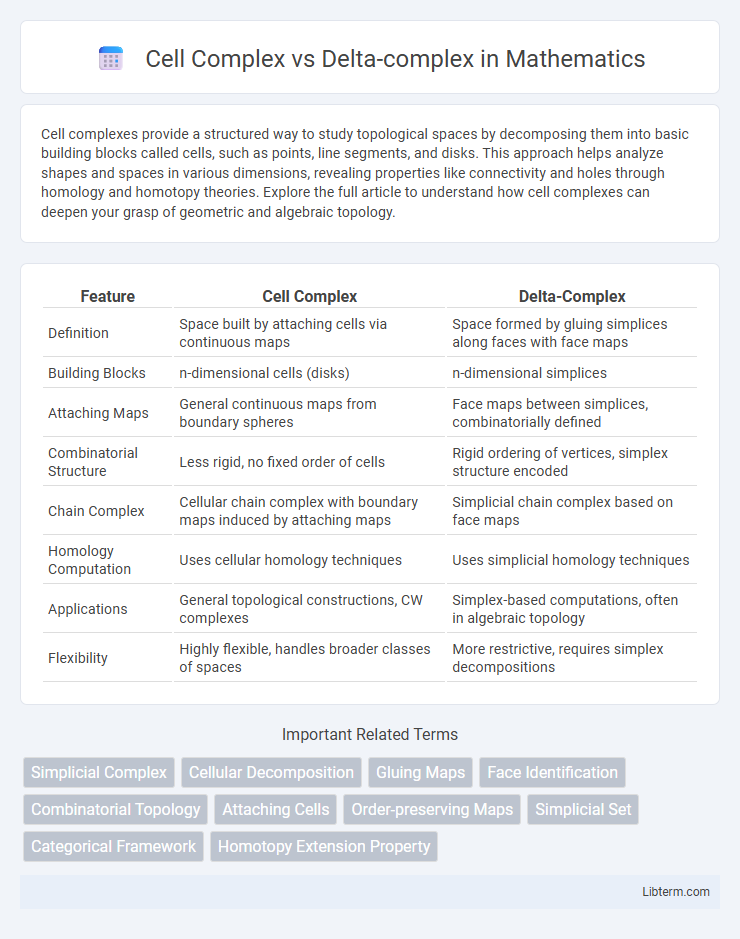
| Feature | Cell Complex | Delta-Complex |
|---|---|---|
| Definition | Space built by attaching cells via continuous maps | Space formed by gluing simplices along faces with face maps |
| Building Blocks | n-dimensional cells (disks) | n-dimensional simplices |
| Attaching Maps | General continuous maps from boundary spheres | Face maps between simplices, combinatorially defined |
| Combinatorial Structure | Less rigid, no fixed order of cells | Rigid ordering of vertices, simplex structure encoded |
| Chain Complex | Cellular chain complex with boundary maps induced by attaching maps | Simplicial chain complex based on face maps |
| Homology Computation | Uses cellular homology techniques | Uses simplicial homology techniques |
| Applications | General topological constructions, CW complexes | Simplex-based computations, often in algebraic topology |
| Flexibility | Highly flexible, handles broader classes of spaces | More restrictive, requires simplex decompositions |
Introduction to Cell Complexes and Delta-complexes
Cell complexes and Delta-complexes are fundamental structures in algebraic topology used to study topological spaces through combinatorial means. A cell complex is built by successively attaching n-dimensional cells to lower-dimensional skeletons using continuous maps, enabling the decomposition of spaces into basic building blocks. Delta-complexes refine this concept by imposing simplicial structures with ordered vertices, allowing for combinatorial manipulations based on simplices and face maps.
Historical Background and Development
Cell complexes originated from early 20th-century topological research, with Henri Poincare's work laying foundational concepts in algebraic topology. Delta-complexes emerged as a refinement introduced by J.H.C. Whitehead in the mid-20th century, aiming to simplify computations by using ordered simplices glued along faces. The development of delta-complexes provided a more combinatorial approach, facilitating advancements in simplicial homology while maintaining the generality of cell complexes.
Formal Definitions of Cell Complex and Delta-complex
A cell complex is a topological space constructed by inductively attaching n-dimensional cells via continuous maps from the boundary of the n-cell to the (n-1)-skeleton, forming a CW-complex with closure-finite and weak topology properties. A delta-complex is a combinatorial object where simplices are glued together along face maps defined by injective order-preserving functions from standard simplices, generating a simplicial set structure without degeneracies. While a cell complex allows arbitrary attaching maps and flexible cell shapes, a delta-complex formalizes the gluing of simplices with an emphasis on ordered combinatorial data and face identifications.
Building Blocks: Cells vs Simplices
Cell complexes are constructed from cells, which are topological spaces homeomorphic to open balls of various dimensions, allowing more general shapes beyond simplices. Delta-complexes specifically use simplices--the building blocks that are standard geometric triangles, tetrahedra, and their higher-dimensional analogs--glued together via face maps following a strict combinatorial pattern. This distinction enables cell complexes greater flexibility in modeling spaces, while delta-complexes provide a more algebraically tractable framework grounded in simplicial geometry.
Attachment Maps: Rules and Restrictions
Attachment maps in cell complexes must be continuous functions from the boundary of an n-cell, typically an (n-1)-sphere, to the existing complex, ensuring the cell is attached via closed, well-defined neighborhoods without overlaps that violate the Hausdorff condition. Delta-complexes use simplicial attachment maps that are face inclusions preserving the order of vertices, enforcing strict combinatorial rules that simplify homological computations but restrict the types of gluing allowed. These restrictions in delta-complexes guarantee that each simplex is attached along a union of its faces via injective maps, contrasting with the more flexible but topologically intricate attachment maps permitted in general cell complexes.
Examples of Cell Complexes
Cell complexes include CW complexes like spheres, tori, and projective planes formed by gluing cells of varying dimensions together, such as attaching 2-disks to 1-skeletons. Delta-complexes, used primarily in algebraic topology, represent spaces with simplices glued via face maps, exemplified by standard triangulations of surfaces. Notable examples of cell complexes are the 2-sphere constructed from one 0-cell and one 2-cell or the torus formed by attaching a 2-cell to a wedge of two circles in a prescribed manner.
Examples of Delta-complexes
Delta-complexes provide a combinatorial model for topological spaces built from simplices by specifying how faces are glued together, commonly illustrated by the standard 2-simplex and the triangulated torus. Unlike general cell complexes, delta-complexes restrict gluings to simplices via order-preserving maps, enabling clear descriptions of spaces such as wedge sums of circles or surfaces with polygonal boundaries. Examples include the triangulation of the Klein bottle using a delta-complex structure and the realization of complex projective spaces through iterated simplicial constructions.
Applications in Algebraic Topology
Cell complexes provide a flexible framework for constructing topological spaces by attaching cells of various dimensions, which aids in computing homology and cohomology groups. Delta-complexes, a specialized form of simplicial complexes, offer combinatorial convenience by encoding spaces with explicit simplicial structures, simplifying the calculation of fundamental groups and singular homology. Applications in algebraic topology leverage these structures to analyze space decomposition, enabling efficient computation of invariants used in classification and mapping problems.
Advantages and Limitations of Each Structure
Cell complexes provide a flexible framework for constructing topological spaces by gluing cells of various dimensions, offering greater generality and applicability in modeling complex geometries. Delta-complexes simplify computations by restricting attachments to simplices with ordered vertices, making homology calculations more explicit but less adaptable to irregular topologies. While cell complexes handle a broader class of spaces with potentially non-simplicial structure, delta-complexes benefit from combinatorial clarity and easier algorithmic implementation at the cost of reduced expressive power.
Conclusion: Choosing Between Cell Complex and Delta-complex
Choosing between a cell complex and a delta-complex depends on the specific requirements of topological modeling and combinatorial structure. Cell complexes provide greater flexibility with general cells and diverse attaching maps, making them suitable for complex geometric configurations and higher-dimensional manifolds. Delta-complexes offer a more rigid simplicial structure, which simplifies computations and theoretical analysis, especially in algebraic topology and homology calculations.
Cell Complex Infographic
 libterm.com
libterm.com