Matrix algebra is a fundamental branch of mathematics focusing on the manipulation and analysis of matrices, which are rectangular arrays of numbers or symbols. It plays a critical role in solving systems of linear equations, transformations in computer graphics, and various applications across engineering and data science. Explore this article to deepen your understanding of matrix algebra and how it can enhance your problem-solving skills.
Table of Comparison
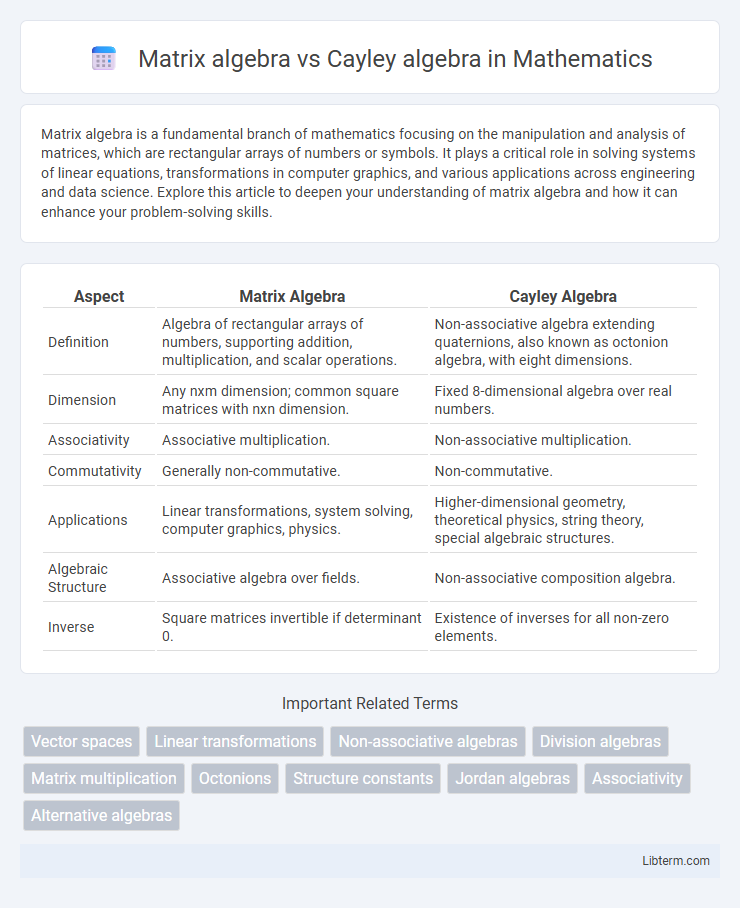
| Aspect | Matrix Algebra | Cayley Algebra |
|---|---|---|
| Definition | Algebra of rectangular arrays of numbers, supporting addition, multiplication, and scalar operations. | Non-associative algebra extending quaternions, also known as octonion algebra, with eight dimensions. |
| Dimension | Any nxm dimension; common square matrices with nxn dimension. | Fixed 8-dimensional algebra over real numbers. |
| Associativity | Associative multiplication. | Non-associative multiplication. |
| Commutativity | Generally non-commutative. | Non-commutative. |
| Applications | Linear transformations, system solving, computer graphics, physics. | Higher-dimensional geometry, theoretical physics, string theory, special algebraic structures. |
| Algebraic Structure | Associative algebra over fields. | Non-associative composition algebra. |
| Inverse | Square matrices invertible if determinant 0. | Existence of inverses for all non-zero elements. |
Introduction to Matrix Algebra and Cayley Algebra
Matrix algebra studies rectangular arrays of numbers with operations like addition, multiplication, and inversion central to linear transformations and system solving. Cayley algebra, an example of a normed division algebra, extends complex numbers through octonions featuring nonassociative properties with applications in theoretical physics and geometry. Both algebras serve distinct roles: matrix algebra facilitates practical computation in vector spaces, while Cayley algebra underpins abstract algebraic structures.
Historical Development of Both Algebras
Matrix algebra originated in the 19th century through the works of Arthur Cayley and James Joseph Sylvester, formalizing the manipulation of arrays of numbers to solve linear equations and transformations. Cayley algebra, also known as the algebra of octonions, was developed later in the late 19th century by Arthur Cayley and John T. Graves as an extension of quaternions, introducing non-associative multiplication in an eight-dimensional number system. Both algebras significantly influenced modern mathematics by providing fundamental frameworks for abstract algebra, with matrix algebra becoming essential in linear algebra and Cayley algebra pioneering studies in non-associative algebras.
Fundamental Concepts and Definitions
Matrix algebra centers on operations involving matrices, such as addition, multiplication, and inversion, emphasizing linear transformations and vector space properties. Cayley algebra, or Cayley-Dickson construction, generalizes complex numbers and quaternions to create higher-dimensional algebras like octonions, characterized by non-associative multiplication and normed division properties. Fundamental concepts in matrix algebra include determinants, eigenvalues, and rank, whereas Cayley algebra focuses on basis elements, multiplication rules, and algebraic structures extending beyond associative norms.
Structure and Operations in Matrix Algebra
Matrix algebra revolves around the manipulation of matrices using operations such as addition, multiplication, and inversion, emphasizing properties like associativity and distributivity. It operates within a well-defined structure of vector spaces and linear transformations, facilitating solutions to systems of linear equations and eigenvalue problems. In contrast, Cayley algebra extends these concepts to non-associative algebras like octonions, where the multiplication operation lacks associativity but retains other algebraic properties.
Structure and Operations in Cayley Algebra
Cayley algebra, also known as the algebra of octonions, is a non-associative extension of complex numbers characterized by an eight-dimensional vector space over the real numbers. Unlike matrix algebra, which is associative and based on operations such as matrix multiplication and addition, Cayley algebra uses a multiplication operation that is non-associative but alternative, meaning it satisfies weaker associativity-like conditions. The structure of Cayley algebra includes a norm and conjugation operation, enabling division but requiring a more complex approach to operations and inverses compared to the straightforward linear transformations inherent in matrix algebra.
Differences in Algebraic Properties
Matrix algebra involves the study of linear transformations represented by matrices, primarily focusing on associative multiplication where the product of two matrices depends on the order but satisfies (AB)C = A(BC). Cayley algebra, also known as octonion algebra, is a non-associative algebra extending quaternions, where multiplication is neither associative nor commutative, exhibiting alternative properties instead. The key difference lies in associativity: matrix algebra maintains strict associativity, while Cayley algebra is non-associative but alternative, impacting their applications in various mathematical and physical contexts.
Applications in Science and Engineering
Matrix algebra underpins numerous applications in science and engineering, including systems of linear equations, computer graphics transformations, and stability analysis in control systems. Cayley algebra, particularly through the Cayley-Dickson construction, extends matrix concepts to non-associative structures used in theoretical physics, robotics, and computer vision for modeling rotations and quantum computations. These algebras provide distinct yet complementary frameworks for solving complex problems involving multidimensional data and symmetry operations.
Computational Aspects and Complexities
Matrix algebra involves operations on arrays of numbers with well-established computational algorithms, where complexities depend on matrix size n, typically O(n^3) for multiplication using classical methods, while advanced techniques like Strassen's algorithm reduce this to approximately O(n^2.81). Cayley algebra, as an extension of quaternion and octonion algebras, introduces non-associativity and higher-dimensional hypercomplex numbers, increasing computational complexity due to less straightforward multiplication rules and the necessity for specialized algorithms. The computational efficiency of matrix algebra often surpasses Cayley algebra in numerical linear algebra tasks, though Cayley algebra offers advantages in specific applications like 3D rotations and theoretical physics where non-commutative properties are essential.
Advantages and Limitations
Matrix algebra offers efficient computation and well-established numerical methods for linear transformations, making it ideal for computer graphics and engineering applications. Cayley algebra, which generalizes complex numbers and quaternions, excels in representing rotations and orientations in higher dimensions with fewer singularities. However, matrix algebra can become computationally intensive in very high dimensions, whereas Cayley algebra's abstract structure may limit its straightforward applicability in standard linear algebra problems.
Conclusion and Future Perspectives
Matrix algebra offers a well-established framework with extensive applications in linear transformations, quantum mechanics, and computer graphics, whereas Cayley algebra introduces non-associative elements that extend classical algebraic structures and provide insights into octonions and higher-dimensional number systems. Future perspectives highlight the potential for Cayley algebra to enrich theoretical physics, particularly in string theory and exceptional Lie groups, while advancements in matrix algebra continue to drive innovations in machine learning and data analysis. Bridging these algebras could lead to novel computational techniques and a deeper understanding of symmetry and structure in mathematics and physics.
Matrix algebra Infographic
 libterm.com
libterm.com