Fiber bundles are intricate structures in mathematics that consist of a base space, a total space, and a projection map connecting the two, with each point in the base space having a fiber attached. These bundles play a crucial role in topology and geometry by allowing the study of spaces locally resembling a product space while possessing a more complex global structure. Explore the rest of the article to understand how fiber bundles influence modern mathematical theories and applications.
Table of Comparison
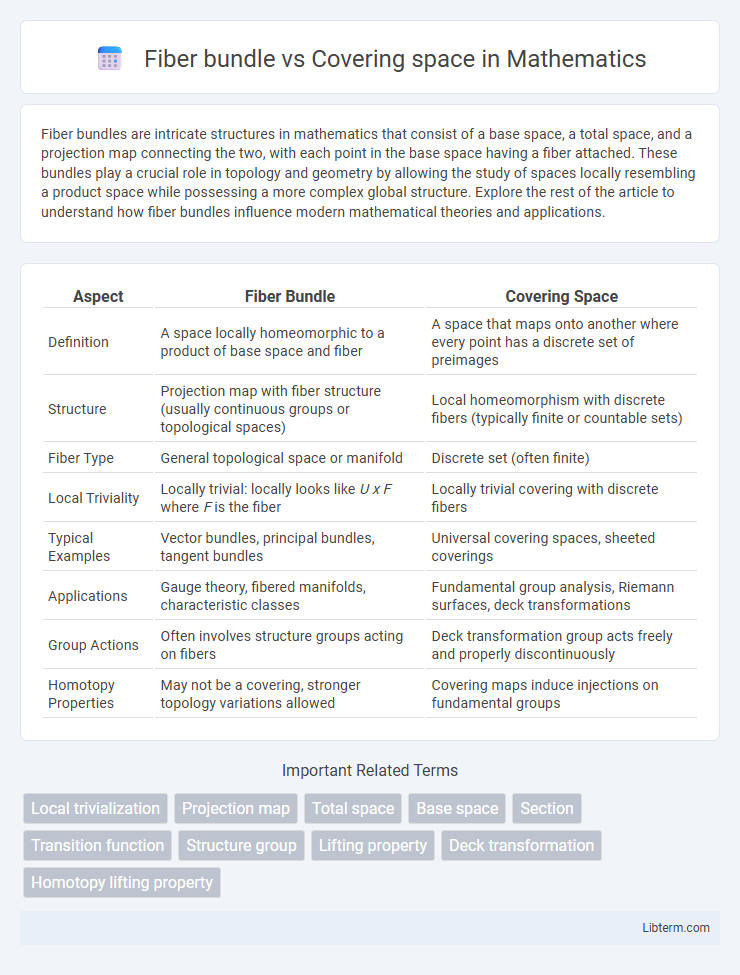
| Aspect | Fiber Bundle | Covering Space |
|---|---|---|
| Definition | A space locally homeomorphic to a product of base space and fiber | A space that maps onto another where every point has a discrete set of preimages |
| Structure | Projection map with fiber structure (usually continuous groups or topological spaces) | Local homeomorphism with discrete fibers (typically finite or countable sets) |
| Fiber Type | General topological space or manifold | Discrete set (often finite) |
| Local Triviality | Locally trivial: locally looks like U x F where F is the fiber | Locally trivial covering with discrete fibers |
| Typical Examples | Vector bundles, principal bundles, tangent bundles | Universal covering spaces, sheeted coverings |
| Applications | Gauge theory, fibered manifolds, characteristic classes | Fundamental group analysis, Riemann surfaces, deck transformations |
| Group Actions | Often involves structure groups acting on fibers | Deck transformation group acts freely and properly discontinuously |
| Homotopy Properties | May not be a covering, stronger topology variations allowed | Covering maps induce injections on fundamental groups |
Introduction to Fiber Bundles and Covering Spaces
Fiber bundles and covering spaces are fundamental concepts in topology, where a fiber bundle consists of a total space, base space, and a typical fiber with a continuous surjective projection exhibiting local triviality. Covering spaces are special cases of fiber bundles with discrete fibers and unique path lifting properties, often used to study the fundamental group of the base space. Understanding fiber bundles involves grasping local product structures and transition functions, while covering spaces emphasize deck transformations and lifting criteria.
Fundamental Definitions
A fiber bundle is a topological space that locally looks like a product space but may have a different global structure, defined by a continuous surjection p: E - B with fiber F and base space B such that for every b in B, there exists a neighborhood U where p^-1(U) is homeomorphic to U x F. A covering space is a special case of a fiber bundle where the fiber is a discrete set, and the map p is a local homeomorphism with evenly covered neighborhoods in the base space. Both concepts involve projections onto base spaces, but fiber bundles emphasize local product structures with continuous fibers, while covering spaces focus on discrete fiber and lifting properties.
Key Differences: Fiber Bundles vs Covering Spaces
Fiber bundles feature a continuous surjective map with typical fibers resembling a fixed space and local triviality resembling a product structure, while covering spaces specifically have discrete fibers and local homeomorphisms allowing unique path lifting. The structure group in fiber bundles can be any topological group acting on the fiber, whereas covering spaces correspond to actions of discrete groups, often related to the fundamental group of the base space. Fiber bundles are generalizations including vector bundles and principal bundles, while covering spaces form a special class characterized by evenly covered neighborhoods and unique lifting properties.
Structure and Local Triviality
Fiber bundles consist of a total space mapped onto a base space such that each fiber resembles a typical fiber space, maintaining local triviality by appearing as a product of the base and the fiber. Covering spaces are a special case of fiber bundles where the fiber is discrete, and the projection map is locally homeomorphic, ensuring local triviality as trivial covering maps over open neighborhoods. The key structural difference lies in the type of fibers: fiber bundles allow continuous, typically manifold-like fibers, while covering spaces have discrete fibers with a lifting property fundamental to algebraic topology.
Examples of Fiber Bundles
Examples of fiber bundles include the Mobius strip, which serves as a non-trivial line bundle over the circle S^1, and the Hopf fibration, a principal bundle with fiber S^1 over the base space S^2. Tangent bundles of smooth manifolds provide another key example, where the fiber consists of tangent spaces attached smoothly to each point of the manifold. Unlike covering spaces, fiber bundles allow fibers with more complex structure than discrete sets, enabling richer topological and geometric constructions.
Examples of Covering Spaces
Covering spaces include classic examples such as the universal cover of the circle \( S^1 \), represented by the real line \( \mathbb{R} \) with the covering map \( p: \mathbb{R} \to S^1 \) defined by \( p(t) = e^{2\pi it} \). Another fundamental example is the torus \( T^2 \), which can be viewed as a covering space over itself via the map induced by integer lattice translations on \( \mathbb{R}^2 \). These examples illustrate how covering spaces provide locally homeomorphic surjective maps that are discrete and evenly cover the base space, differing from general fiber bundles by their emphasis on lifting properties and local biholomorphic structure.
Applications in Topology and Geometry
Fiber bundles enable the systematic study of spaces by providing local product structures, crucial for classifying vector bundles and principal bundles in differential geometry. Covering spaces facilitate the analysis of fundamental groups and provide tools for lifting properties, essential in algebraic topology for understanding space connectivity and homotopy. Applications in topology and geometry leverage fiber bundles for gauge theory and characteristic classes, while covering spaces support universal covers and deck transformations in manifold theory.
Homotopy and Lifting Properties
Fiber bundles and covering spaces differ primarily in their homotopy lifting properties, where covering spaces guarantee unique path lifting and homotopy lifting for any space, ensuring that fibers are discrete and typically totally disconnected. Fiber bundles generalize this concept by allowing fibers to be more complex spaces, with homotopy lifting holding locally but not necessarily globally, requiring additional structure such as a connection for unique lifting. The distinction is crucial in algebraic topology, as covering spaces correspond to principal G-bundles with discrete structure group G, while fiber bundles accommodate continuous groups, impacting their classification via homotopy groups and lifting criteria.
Visualizing Fiber Bundles and Covering Spaces
Fiber bundles are visualized as a space appearing locally like a product of a base space and a typical fiber, where each fiber smoothly varies over the base, such as a Mobius strip depicted as a twisted bundle over a circle. Covering spaces can be represented by multiple sheets or layers evenly projecting onto the base space, like a multi-layered spiral staircase covering a circle. Both structures encode topological information, but fiber bundles emphasize smooth local trivializations with structured fibers, whereas covering spaces focus on discrete sheeted projections preserving local homeomorphisms.
Choosing Between Fiber Bundles and Covering Spaces
Choosing between fiber bundles and covering spaces depends on the complexity and structure of the space in question; fiber bundles provide a richer framework for spaces with varying fibers and allow for the study of local trivializations and transition functions, essential in differential geometry and topology. Covering spaces are more specialized, focusing on locally homeomorphic projections with discrete fibers, primarily useful in algebraic topology for analyzing fundamental groups and lifting properties. Understanding the nature of the fibers and the desired topological or geometric properties guides the decision, with fiber bundles favored for applications requiring smoothness and structure group actions, while covering spaces excel in situations demanding simpler, discrete layer decompositions.
Fiber bundle Infographic
 libterm.com
libterm.com