Range defines the span between the minimum and maximum values in a data set, providing a simple measure of variability. Understanding range helps you quickly grasp the spread of your data, which is essential for statistical analysis and decision-making. Explore the full article to discover practical examples and how range compares to other measures of dispersion.
Table of Comparison
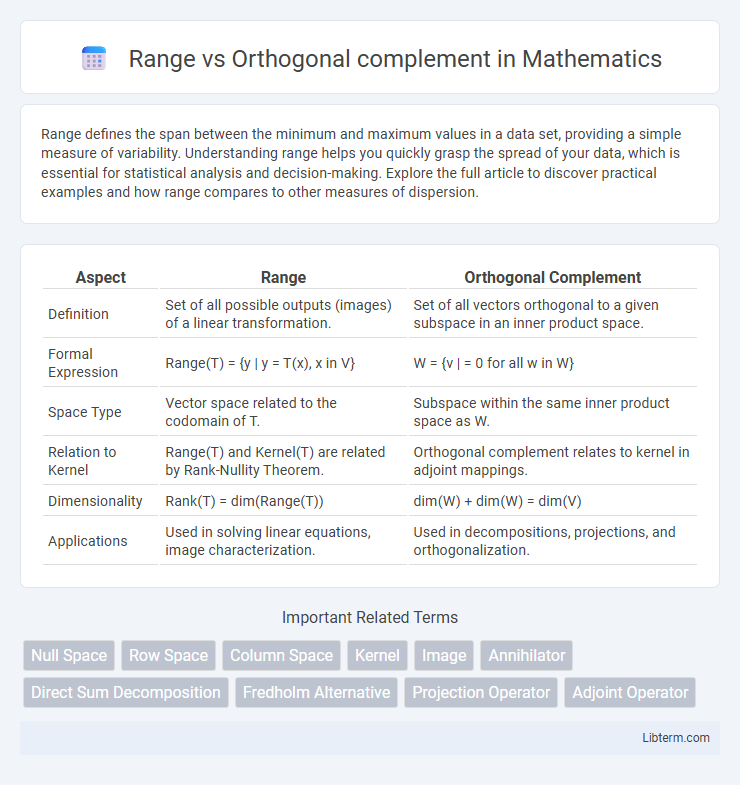
| Aspect | Range | Orthogonal Complement |
|---|---|---|
| Definition | Set of all possible outputs (images) of a linear transformation. | Set of all vectors orthogonal to a given subspace in an inner product space. |
| Formal Expression | Range(T) = {y | y = T(x), x in V} | W = {v | |
| Space Type | Vector space related to the codomain of T. | Subspace within the same inner product space as W. |
| Relation to Kernel | Range(T) and Kernel(T) are related by Rank-Nullity Theorem. | Orthogonal complement relates to kernel in adjoint mappings. |
| Dimensionality | Rank(T) = dim(Range(T)) | dim(W) + dim(W) = dim(V) |
| Applications | Used in solving linear equations, image characterization. | Used in decompositions, projections, and orthogonalization. |
Introduction to Range and Orthogonal Complement
The range of a linear operator or matrix represents all possible outputs or vectors that can be expressed as a linear combination of the operator's columns, defining the span of its action. The orthogonal complement consists of all vectors that are perpendicular to every vector in a given subspace, including the range, characterizing directions that yield zero inner product with the subspace elements. Understanding these concepts is fundamental in linear algebra as they underpin key results such as the Fundamental Theorem of Linear Algebra, linking the dimensions and relationships between subspaces.
Definitions: Range and Orthogonal Complement Explained
The range of a linear operator or matrix refers to the set of all possible output vectors it can produce, representing the span of its column vectors. The orthogonal complement of a subspace consists of all vectors that are perpendicular to every vector in that subspace, capturing the idea of orthogonality within vector spaces. Understanding the range and orthogonal complement is crucial for solving systems of linear equations and analyzing vector space structures.
The Role of Inner Products in Orthogonality
Inner products define orthogonality by measuring the zero angle between vectors, which underpins the concept of the orthogonal complement as the set of all vectors orthogonal to a given subspace. The range of a linear operator relates to its orthogonal complement through the fundamental theorem of linear algebra, where the orthogonal complement of the range space corresponds to the null space of the adjoint operator. Understanding inner products allows precise characterization of subspace decompositions, enabling projections onto the range and orthogonal complements essential in functional analysis and signal processing.
Properties of Range in Linear Transformations
The range of a linear transformation T: V - W is the set of all vectors in W that can be expressed as T(v) for some v in V, forming a subspace of W. It characterizes the image or output space of T, reflecting the dimension as the rank of T. The range's relationship with the orthogonal complement of the null space is fundamental in the rank-nullity theorem, highlighting how the range's dimension plus the dimension of the null space equals the dimension of V.
Understanding Orthogonal Complements in Vector Spaces
Orthogonal complements in vector spaces consist of all vectors orthogonal to a given subspace, providing a fundamental tool for decomposing spaces into perpendicular components. The range of a linear operator represents all possible outputs, while the orthogonal complement of this range captures vectors that the operator maps to zero, revealing insights into null spaces and solution uniqueness. Mastering the relationship between range and orthogonal complements enriches understanding of projections, least squares approximations, and eigenvalue problems in linear algebra.
Relationship Between Range and Orthogonal Complement
The range of a linear operator T on a Hilbert space is closely related to its orthogonal complement, as the orthogonal complement of the range is the null space of the adjoint operator T*. This relationship can be expressed by the fundamental identity (Range(T)) = Null(T*), which is central in functional analysis and operator theory. Understanding this duality helps characterize projections, solve linear equations, and analyze the structure of linear transformations in inner product spaces.
Applications in Solving Linear Equations
The Range and Orthogonal Complement concepts play crucial roles in solving linear equations, particularly in determining solution existence and uniqueness. The Range (or column space) of a matrix contains all possible output vectors for the linear transformation, helping identify if a system is consistent by checking if the target vector lies within this subspace. The Orthogonal Complement, often linked to the null space of the transpose matrix, aids in characterizing solution sets by identifying all vectors orthogonal to the range, which is essential in least squares solutions to overdetermined systems.
Geometric Interpretation and Visualization
The range of a linear transformation represents all possible output vectors, visualized as a subspace where the transformation projects inputs. The orthogonal complement consists of vectors perpendicular to every vector in the range, forming a subspace that spans the space outside the range. Geometrically, these two subspaces are perpendicular and together cover the entire vector space, enabling decomposition of any vector into components aligned with the range and orthogonal complement.
Role in Least Squares and Projections
The range of a matrix A represents all possible linear combinations of its columns, directly corresponding to the set of attainable outputs in linear transformations, essential for understanding the column space in least squares problems. The orthogonal complement to this range, known as the null space of AT, captures vectors orthogonal to the range, defining the residual error in least squares approximations. Projections onto the range minimize the error norm by decomposing vectors into components parallel and orthogonal to the range, facilitating optimal solutions in projection-based methods.
Summary of Key Differences and Connections
The range of a linear transformation consists of all possible output vectors, while the orthogonal complement includes all vectors orthogonal to a given subspace, typically the range's orthogonal complement contains vectors orthogonal to the range. The range and its orthogonal complement intersect only at the zero vector, highlighting their perpendicular nature in vector space decomposition. In finite-dimensional inner product spaces, the entire space can be expressed as the direct sum of the range and its orthogonal complement.
Range Infographic
 libterm.com
libterm.com