The Gaussian function is a fundamental concept in mathematics and statistics, characterized by its symmetric bell-shaped curve representing the normal distribution. Widely used in data analysis, signal processing, and machine learning, it models random variables with a specific mean and variance. Explore the rest of the article to understand how the Gaussian function can enhance your data interpretation and predictive modeling.
Table of Comparison
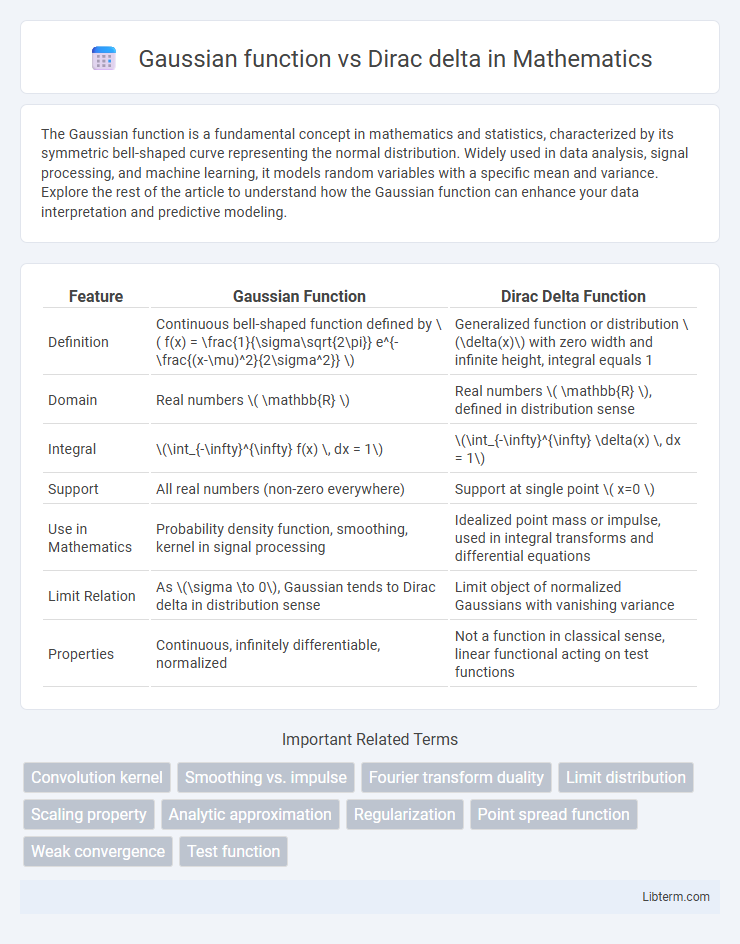
| Feature | Gaussian Function | Dirac Delta Function |
|---|---|---|
| Definition | Continuous bell-shaped function defined by \( f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}} \) | Generalized function or distribution \(\delta(x)\) with zero width and infinite height, integral equals 1 |
| Domain | Real numbers \( \mathbb{R} \) | Real numbers \( \mathbb{R} \), defined in distribution sense |
| Integral | \(\int_{-\infty}^{\infty} f(x) \, dx = 1\) | \(\int_{-\infty}^{\infty} \delta(x) \, dx = 1\) |
| Support | All real numbers (non-zero everywhere) | Support at single point \( x=0 \) |
| Use in Mathematics | Probability density function, smoothing, kernel in signal processing | Idealized point mass or impulse, used in integral transforms and differential equations |
| Limit Relation | As \(\sigma \to 0\), Gaussian tends to Dirac delta in distribution sense | Limit object of normalized Gaussians with vanishing variance |
| Properties | Continuous, infinitely differentiable, normalized | Not a function in classical sense, linear functional acting on test functions |
Introduction to Gaussian Function and Dirac Delta
The Gaussian function is a continuous, smooth bell-shaped curve characterized by its mean and variance, widely used in probability, statistics, and signal processing for modeling normal distributions and smoothing data. In contrast, the Dirac delta is a generalized function or distribution that represents an idealized point mass or impulse, with zero width and infinite height, integrating to one over its entire domain. While the Gaussian function serves as a practical approximation, the Dirac delta functions as a theoretical tool for sampling and impulse representation in mathematical physics and engineering.
Mathematical Definitions
The Gaussian function is defined as \( f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}} \), where \(\mu\) is the mean and \(\sigma\) is the standard deviation, forming a continuous function with finite amplitude. The Dirac delta function, denoted \(\delta(x)\), is not a traditional function but a distribution satisfying \(\int_{-\infty}^{\infty} \delta(x) \, dx = 1\) and \(\delta(x) = 0\) for all \(x \neq 0\), mathematically representing an idealized point mass or impulse. Whereas the Gaussian is smooth and integrable with finite width, the Dirac delta approaches the limit of a Gaussian as \(\sigma \to 0\), concentrating all area at a single point.
Key Properties and Characteristics
The Gaussian function is a smooth, continuous function characterized by its bell-shaped curve, defined by the mean and standard deviation, and is widely used in probability and signal processing due to its integrability and finite values. In contrast, the Dirac delta is a distribution, not a function in the classical sense, with an infinitesimal width and infinite peak, used to model point impulses and defined by the sifting property, where its integral over the entire real line equals one. Key differences include the Gaussian's role as a probability density function with spread and smoothness, while the Dirac delta serves as an idealized limit, concentrating all mass at a single point, making it crucial in theoretical physics and engineering.
Visualization and Graphical Interpretation
The Gaussian function appears as a smooth, bell-shaped curve with finite width and height, illustrating continuous values over the entire real line, while the Dirac delta is represented graphically as an infinitely narrow spike at zero with infinite height, embodying an idealized point mass or impulse. Visualization of the Gaussian emphasizes its probabilistic distribution properties and smooth decay on both sides, whereas the Dirac delta visualization highlights its role as a distribution or generalized function that integrates to one but lacks a conventional graph. Graphical interpretation reveals the Gaussian's behavior as a kernel in convolution operations, contrasting with the Dirac delta's function as the identity element in integral transforms like the Fourier transform.
Role in Signal Processing
The Gaussian function serves as a fundamental smoothing filter in signal processing, effectively reducing noise while preserving signal characteristics due to its continuous and bell-shaped curve. In contrast, the Dirac delta acts as an idealized impulse signal used to analyze system responses through convolution, enabling the extraction of system characteristics like impulse response and transfer function. Both functions are pivotal; the Gaussian aids in filtering and feature extraction, whereas the Dirac delta forms the theoretical basis for system identification and sampling.
Application in Probability and Statistics
The Gaussian function, characterized by its bell-shaped curve and defined by mean and variance parameters, models continuous probability distributions such as the normal distribution, essential for statistical inference and hypothesis testing. The Dirac delta function serves as an idealized probability density, representing a degenerate distribution concentrated at a single point, frequently used to model deterministic outcomes or initial conditions in stochastic processes. Together, these functions enable precise representation of uncertainty, with the Gaussian capturing variability and the Dirac delta emphasizing exactness in probabilistic modeling and signal processing.
Limit Relationship: Gaussian Approximating Dirac Delta
The Gaussian function \( g_\sigma(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{x^2}{2\sigma^2}} \) approximates the Dirac delta \(\delta(x)\) as the variance \(\sigma^2\) approaches zero, concentrating all probability mass at the origin. In the limit \(\sigma \to 0\), the Gaussian satisfies the sifting property of the delta distribution, where \(\int_{-\infty}^\infty g_\sigma(x) f(x) \, dx \to f(0)\) for any continuous function \(f\). This limit relationship is fundamental in signal processing and distribution theory, linking smooth approximations to idealized point sources.
Convolution Differences
The Gaussian function is a smooth, continuous function used in convolution to produce blurred or smoothed signals by averaging nearby values with weighted importance decreasing exponentially from the center. The Dirac delta function acts as an identity element under convolution, leaving the original signal unchanged by effectively sampling it at a single point. While Gaussian convolution results in signal smoothing and noise reduction, convolution with the Dirac delta serves as a mathematical idealization to extract instantaneous values without altering the signal's content.
Common Use Cases in Physics and Engineering
The Gaussian function is commonly used in physics and engineering to model probability distributions, heat diffusion, and signal smoothing due to its smooth, bell-shaped curve. The Dirac delta function serves as an idealized impulse in systems analysis, representing point sources or instantaneous events in fields such as quantum mechanics, control theory, and electromagnetics. Both functions play critical roles in Fourier transforms, with the Gaussian function preserving shape under transformation and the Dirac delta acting as the identity element in convolution operations.
Summary and Comparative Analysis
The Gaussian function is a smooth, bell-shaped curve defined by the formula \( f(x) = \frac{1}{\sigma \sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2\sigma^2}} \), commonly used in probability theory and signal processing for modeling continuous distributions with finite variance. The Dirac delta function, denoted \( \delta(x) \), is a generalized function or distribution characterized by being zero everywhere except at zero, where it is infinite, with the integral over the entire real line equal to one, serving as an idealized point mass or impulse. Compared to the Dirac delta, the Gaussian function approaches the delta function in the limit as its standard deviation \( \sigma \) tends to zero, offering a smooth approximation that is mathematically well-defined and widely used in applications requiring a transition between continuous and discrete models.
Gaussian function Infographic
 libterm.com
libterm.com