Szemeredi's theorem is a fundamental result in arithmetic combinatorics, establishing that any subset of the integers with positive density contains arbitrarily long arithmetic progressions. This theorem has profound implications for understanding the structure of sets within number theory and has influenced various areas such as ergodic theory and Ramsey theory. Discover how Szemeredi's theorem shapes modern mathematics and its surprising applications by reading the rest of this article.
Table of Comparison
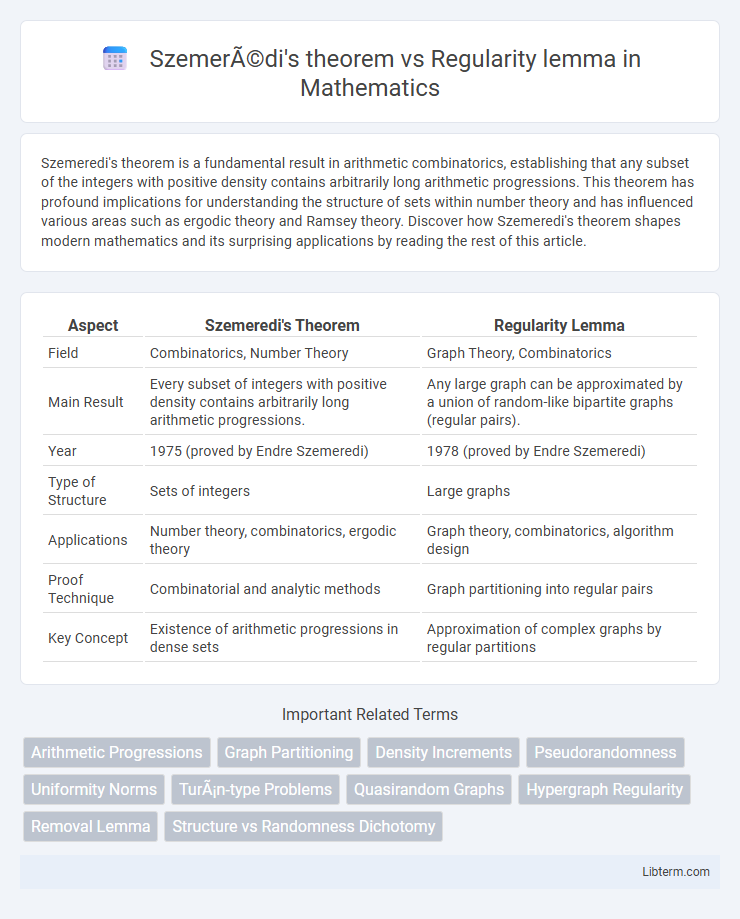
| Aspect | Szemeredi's Theorem | Regularity Lemma |
|---|---|---|
| Field | Combinatorics, Number Theory | Graph Theory, Combinatorics |
| Main Result | Every subset of integers with positive density contains arbitrarily long arithmetic progressions. | Any large graph can be approximated by a union of random-like bipartite graphs (regular pairs). |
| Year | 1975 (proved by Endre Szemeredi) | 1978 (proved by Endre Szemeredi) |
| Type of Structure | Sets of integers | Large graphs |
| Applications | Number theory, combinatorics, ergodic theory | Graph theory, combinatorics, algorithm design |
| Proof Technique | Combinatorial and analytic methods | Graph partitioning into regular pairs |
| Key Concept | Existence of arithmetic progressions in dense sets | Approximation of complex graphs by regular partitions |
Introduction to Szemerédi's Theorem and the Regularity Lemma
Szemeredi's theorem states that any subset of the integers with positive density contains arbitrarily long arithmetic progressions, a fundamental result in additive combinatorics. The Regularity Lemma, introduced by Szemeredi, provides a powerful tool for approximating large graphs by a union of random-like bipartite graphs, enabling the analysis of complex combinatorial structures. Together, these concepts form the backbone of modern combinatorics, linking arithmetic progressions and graph theory through structural regularity.
Historical Context and Significance
Szemeredi's theorem, proved by Endre Szemeredi in 1975, marked a breakthrough in combinatorial number theory by establishing that any subset of the integers with positive density contains arbitrarily long arithmetic progressions. The Regularity Lemma, developed by Endre Szemeredi in 1978, provides a fundamental tool for analyzing large graphs by approximating them with a structured, quasi-random partition. Together, these results shaped modern combinatorics by linking number theory with graph theory, enabling profound advances in understanding the distribution of patterns in large discrete structures.
Statement of Szemerédi’s Theorem
Szemeredi's theorem states that any subset of the integers with positive upper density contains arbitrarily long arithmetic progressions, a fundamental result in additive combinatorics and number theory. This theorem guarantees the existence of k-term arithmetic progressions for any integer k, demonstrating deep structural properties of dense sets of integers. The Regularity Lemma, by Szemeredi, provides a powerful graph partitioning tool essential for combinatorial proofs related to but distinct from the arithmetic progressions guaranteed by Szemeredi's theorem.
Formal Definition of the Regularity Lemma
Szemeredi's Regularity Lemma formalizes the idea that every large enough graph can be partitioned into a bounded number of random-like bipartite subgraphs, called regular pairs, where the edge distribution between vertex subsets is uniform up to a small error. Formally, for every e > 0 and integer t_0, there exists T = T(e, t_0) such that any graph G with at least T vertices admits an e-regular partition of its vertex set into k parts with t_0 <= k <= T, where all but an e-fraction of the pairs are e-regular. This lemma underpins Szemeredi's Theorem by enabling the decomposition of graphs into structured components that control arithmetic progression densities in subsets of integers.
Core Ideas: Arithmetic Progressions vs. Graph Regularity
Szemeredi's theorem asserts that any subset of the integers with positive density contains arbitrarily long arithmetic progressions, highlighting the deep structure within number theory and combinatorics. The Regularity Lemma, developed by Endre Szemeredi, provides a powerful tool for approximating large graphs by a union of random-like bipartite graphs, capturing graph regularity and enabling analysis of complex structures. While Szemeredi's theorem focuses on finding arithmetic progressions in dense sets, the Regularity Lemma generalizes these combinatorial insights to graph theory, facilitating the study of irregularities through partitioning into quasi-random components.
Proof Techniques: Combinatorial vs. Analytical Approaches
Szemeredi's theorem primarily employs combinatorial proof techniques, using intricate combinatorial constructions and density arguments to establish the existence of arithmetic progressions within dense subsets of integers. In contrast, the Regularity lemma relies on analytical approaches, utilizing graph theory and measure theory concepts to approximate large graphs with random-like structures, facilitating the study of their global properties. While Szemeredi's combinatorial methods focus on discrete configurations, the Regularity lemma's analytical techniques provide a powerful tool for decomposing complex graphs into simpler, quasi-random components.
Interrelationship and Mutual Implications
Szemeredi's theorem guarantees the existence of long arithmetic progressions in dense subsets of integers, while the Regularity Lemma provides a structural decomposition of large graphs into quasi-random components. The Regularity Lemma plays a crucial role in simplifying the combinatorial framework to prove Szemeredi's theorem by enabling the translation of number-theoretic problems into graph-theoretic settings. Mutual implications arise as advancements in the Regularity Lemma's techniques influence deeper understanding and generalizations of Szemeredi-type results in additive combinatorics and graph theory.
Applications in Combinatorics and Number Theory
Szemeredi's theorem, a cornerstone in additive combinatorics, guarantees the existence of long arithmetic progressions within dense subsets of integers, with profound implications in number theory such as proving that primes contain arbitrarily long arithmetic progressions. The Regularity lemma, a powerful tool in graph theory, enables the partitioning of large graphs into pseudo-random components, facilitating the analysis of complex combinatorial structures and proving results in extremal graph theory and property testing. Both results intersect in combinatorics and number theory by enabling the decomposition and understanding of large, complex sets or graphs, driving advances in analyzing uniformity and structure in discrete mathematics.
Extensions and Generalizations
Szemeredi's theorem, which guarantees the existence of arithmetic progressions in dense subsets of integers, has been extensively extended to various algebraic and combinatorial structures, including polynomial progressions and multidimensional settings. The Regularity lemma, particularly Szemeredi's Regularity lemma, has been generalized to hypergraphs and sparse graphs, enabling analysis of complex combinatorial patterns beyond simple graphs. These extensions collectively enhance tools for understanding uniformity and structure in large discrete systems and have applications in number theory, ergodic theory, and theoretical computer science.
Open Problems and Future Directions
Szemeredi's theorem and the Regularity lemma are foundational in combinatorics, yet several open problems remain, such as finding effective bounds for Szemeredi's theorem and improving the quantitative aspects of the Regularity lemma. Future research aims to refine polynomial bounds and develop constructive algorithms to enhance practical applications in graph theory and number theory. Delving into multidimensional generalizations and extensions to sparse structures represents a promising direction for advancing both theoretical insights and computational methods.
Szemerédi's theorem Infographic
 libterm.com
libterm.com