Non-bijective functions lack the one-to-one correspondence between elements of their domain and codomain, resulting in either non-injective or non-surjective mappings. This property affects how data or elements are paired and can influence outcomes in mathematical modeling or computer science. Explore the rest of this article to understand the implications of non-bijective functions on your work.
Table of Comparison
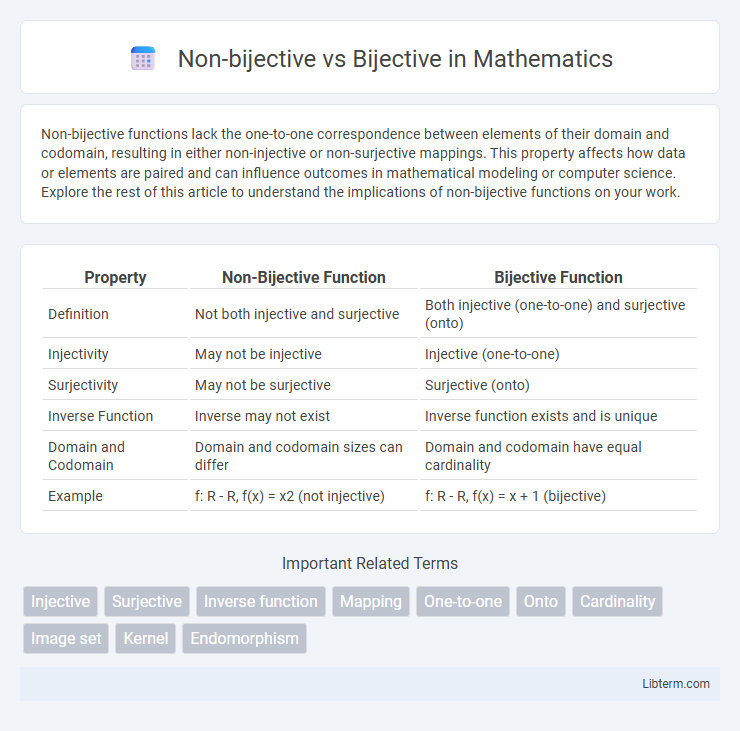
| Property | Non-Bijective Function | Bijective Function |
|---|---|---|
| Definition | Not both injective and surjective | Both injective (one-to-one) and surjective (onto) |
| Injectivity | May not be injective | Injective (one-to-one) |
| Surjectivity | May not be surjective | Surjective (onto) |
| Inverse Function | Inverse may not exist | Inverse function exists and is unique |
| Domain and Codomain | Domain and codomain sizes can differ | Domain and codomain have equal cardinality |
| Example | f: R - R, f(x) = x2 (not injective) | f: R - R, f(x) = x + 1 (bijective) |
Understanding Bijective and Non-Bijective Functions
Bijective functions establish a perfect one-to-one correspondence between elements of the domain and codomain, ensuring both injectivity (no two distinct domain elements map to the same codomain element) and surjectivity (every codomain element is mapped by some domain element). Non-bijective functions fail to satisfy one or both of these properties, resulting in functions that are either not one-to-one (non-injective) or not onto (non-surjective). Understanding these differences is crucial in fields like linear algebra, cryptography, and data mapping, where precise function behavior impacts invertibility and data integrity.
Key Differences Between Bijective and Non-Bijective Functions
Bijective functions create a one-to-one correspondence between elements of the domain and codomain, ensuring both injectivity (no two inputs map to the same output) and surjectivity (every element in the codomain is mapped). Non-bijective functions lack this dual property, as they can be either injective without being surjective or surjective without being injective, resulting in incomplete or overlapping mappings. The key difference lies in bijective functions enabling reversible mappings and thus invertibility, while non-bijective functions do not guarantee an inverse due to missing injective or surjective characteristics.
Mathematical Definitions and Properties
A bijective function is both injective (one-to-one) and surjective (onto), ensuring every element in the codomain corresponds to exactly one element in the domain, which guarantees the existence of an inverse function. A non-bijective function fails to meet either injectivity, surjectivity, or both, meaning it may map multiple domain elements to a single codomain element or leave some codomain elements without a preimage. In mathematical analysis and set theory, bijective functions establish isomorphisms between sets, preserving structure, while non-bijective functions do not provide such perfect correspondence.
Real-World Examples of Bijective Functions
Bijective functions establish a one-to-one correspondence between elements of the domain and codomain, ensuring each input maps to a unique output and every output has a unique input. Real-world examples include telephone number assignments in a city where each number corresponds to exactly one subscriber, and encryption-decryption processes in cryptography where every encrypted message uniquely corresponds to one plaintext. These practical applications highlight the importance of bijective functions in ensuring precise, reversible mappings without ambiguity or data loss.
Practical Applications of Non-Bijective Mappings
Non-bijective mappings, which include injective and surjective functions that are not both one-to-one and onto, are essential in data compression algorithms where multiple inputs map to a single output to reduce storage. In cryptographic hash functions, non-bijective mappings ensure security by allowing numerous possible inputs to produce the same hash value, preventing reverse engineering. These mappings also play a critical role in machine learning models for feature reduction, enabling simplification without requiring an exact one-to-one correspondence between features and outputs.
Visualizing Bijective vs Non-Bijective Relationships
Visualizing bijective relationships involves mapping each element of one set to a unique element of another set, creating a perfect one-to-one correspondence that allows for reversible transformations. In contrast, non-bijective relationships either map multiple elements to the same target (non-injective) or leave some elements without a counterpart (non-surjective), resulting in lost information or incomplete mappings. Diagrams illustrating bijections show paired elements with exclusive arrows, while non-bijective visuals demonstrate overlapping or missing links, highlighting differences in function invertibility and data preservation.
Impact on Data Mapping and Transformations
Non-bijective functions can lead to data loss or ambiguity during mapping and transformations due to their non-invertible nature, causing multiple inputs to map to the same output or some outputs lacking a pre-image. Bijective functions ensure a one-to-one correspondence between data elements, enabling precise and lossless transformations with reversible mappings. This injective and surjective property of bijections guarantees that every input uniquely maps to an output and vice versa, which is critical for consistent data synchronization and integrity in database migrations and encryption algorithms.
Advantages of Bijective Functions in Cryptography
Bijective functions provide a one-to-one mapping between input and output, ensuring every element in the domain corresponds uniquely to an element in the codomain, which is crucial for secure encryption and decryption processes. This unique reversibility prevents information loss and guarantees that encrypted messages can be accurately decrypted without ambiguity. In cryptographic systems, the bijection property enables strong key management and robust data integrity by maintaining consistent and invertible transformations.
Limitations and Challenges of Non-Bijective Functions
Non-bijective functions face limitations such as non-invertibility, resulting in the inability to uniquely recover input values from outputs, which complicates reverse mapping. This restriction impairs certain applications like cryptography and data compression where unique input-output correspondence is crucial. Furthermore, challenges include potential information loss and ambiguity, hindering precise mathematical modeling and problem-solving tasks that require one-to-one mappings.
Choosing Between Bijective and Non-Bijective Approaches
Choosing between bijective and non-bijective approaches depends on the need for unique and reversible mappings, where bijective functions ensure one-to-one correspondences critical for data integrity and symmetry in cryptography. Non-bijective methods allow many-to-one mappings, useful in compression and hashing where multiple inputs can map to the same output without requiring invertibility. Evaluating the trade-offs between reversibility and efficiency guides the optimal selection for specific applications in mathematics, computing, and data science.
Non-bijective Infographic
 libterm.com
libterm.com