Homology groups are fundamental tools in algebraic topology that classify topological spaces based on their cycles and boundaries, revealing intrinsic structural properties. These groups help identify holes of different dimensions within a space, providing a powerful method for distinguishing between complex shapes. Explore the rest of this article to deepen your understanding of how homology groups function and their applications in mathematics.
Table of Comparison
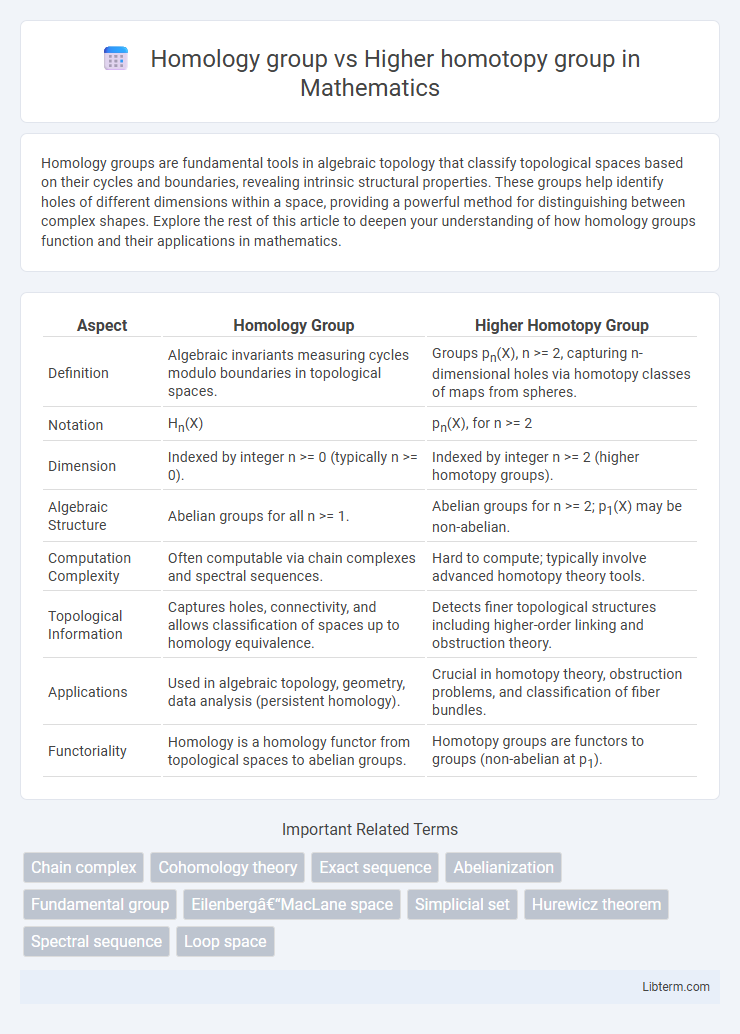
| Aspect | Homology Group | Higher Homotopy Group |
|---|---|---|
| Definition | Algebraic invariants measuring cycles modulo boundaries in topological spaces. | Groups pn(X), n >= 2, capturing n-dimensional holes via homotopy classes of maps from spheres. |
| Notation | Hn(X) | pn(X), for n >= 2 |
| Dimension | Indexed by integer n >= 0 (typically n >= 0). | Indexed by integer n >= 2 (higher homotopy groups). |
| Algebraic Structure | Abelian groups for all n >= 1. | Abelian groups for n >= 2; p1(X) may be non-abelian. |
| Computation Complexity | Often computable via chain complexes and spectral sequences. | Hard to compute; typically involve advanced homotopy theory tools. |
| Topological Information | Captures holes, connectivity, and allows classification of spaces up to homology equivalence. | Detects finer topological structures including higher-order linking and obstruction theory. |
| Applications | Used in algebraic topology, geometry, data analysis (persistent homology). | Crucial in homotopy theory, obstruction problems, and classification of fiber bundles. |
| Functoriality | Homology is a homology functor from topological spaces to abelian groups. | Homotopy groups are functors to groups (non-abelian at p1). |
Introduction to Algebraic Topology: Homology and Homotopy
Homology groups measure the global topological structure of a space by capturing information about holes of different dimensions using chain complexes and boundary operators, producing abelian groups that reflect cycles modulo boundaries. Higher homotopy groups generalize the fundamental group by classifying homotopy classes of maps from higher-dimensional spheres into the space, providing non-abelian invariants that detect more subtle, higher-dimensional connectivity properties. Both concepts form the backbone of algebraic topology, enabling rigorous comparison of topological spaces through algebraic invariants that characterize shape and connectivity beyond intuition.
Defining Homology Groups: Intuition and Formalism
Homology groups measure the algebraic structure of topological spaces by capturing information about cycles and boundaries using chain complexes and homology classes. They are defined through sequences of abelian groups where the boundary operators identify cycles (closed chains) modulo boundaries (exact chains), reflecting holes of various dimensions. Unlike higher homotopy groups, which classify continuous maps from spheres and often have non-abelian structure, homology groups provide computable, abelian invariants that facilitate detecting topological features in a more algebraically tractable manner.
Understanding Higher Homotopy Groups: Beyond Fundamental Group
Higher homotopy groups, denoted \(\pi_n(X)\) for \(n > 1\), capture multi-dimensional loop structures in a topological space \(X\), extending beyond the fundamental group \(\pi_1(X)\) which classifies loops up to homotopy equivalence. Unlike homology groups \(H_n(X)\), which measure cycles and boundaries through abelian groups reflecting topology's "shape" algebraically, higher homotopy groups retain more refined, non-abelian information about the space's higher-dimensional connectivity. Understanding higher homotopy groups involves analyzing maps from \(n\)-spheres into \(X\), revealing intricate properties of \(X\) inaccessible from homology alone.
Key Differences Between Homology and Homotopy Groups
Homology groups classify topological spaces based on cycles and boundaries, capturing holes of different dimensions through abelian groups, while higher homotopy groups measure the multilevel structure of loops and spheres up to homotopy equivalence, often forming non-abelian groups. Homology is computable via chain complexes and is invariant under homotopy, providing algebraic invariants that detect the presence of n-dimensional holes, whereas higher homotopy groups reflect more intricate geometric information about mappings of spheres and the fundamental group's higher-dimensional analogs. Key differences include homology's linearity and abelian nature contrasted with the typically non-abelian and more complex structure of higher homotopy groups, influencing their computational tractability and applications in algebraic topology.
Computational Techniques: Homology vs Higher Homotopy
Computational techniques for homology groups typically utilize boundary operators on chain complexes, enabling efficient calculation through algebraic algorithms such as persistence homology and matrix reduction. In contrast, higher homotopy groups require more intricate computational approaches involving simplicial sets, spectral sequences, or obstruction theory due to their inherently non-abelian structure and the computational complexity of higher-dimensional loops. Software tools like CHomP and Kenzo reflect these differences by providing fast homology computations, while higher homotopy calculations often remain limited to specialized cases through advanced algebraic topology methods.
Examples: Calculating Homology and Higher Homotopy Groups
The homology group of a torus \( T^2 \) is calculated as \( H_0(T^2) \cong \mathbb{Z} \), \( H_1(T^2) \cong \mathbb{Z}^2 \), and \( H_2(T^2) \cong \mathbb{Z} \), revealing its two 1-dimensional holes and one 2-dimensional hole. The higher homotopy groups, such as \( \pi_2(T^2) \), are trivial since the torus is a 2-dimensional manifold, while spheres like \( S^2 \) have \( \pi_2(S^2) \cong \mathbb{Z} \), illustrating nontrivial second homotopy groups. Calculating homology groups employs simplicial or singular homology techniques with chain complexes, whereas higher homotopy groups are typically deduced via obstruction theory or long exact sequences in homotopy.
Applications in Topology: Uses of Each Group
Homology groups quantify topological spaces by measuring cycles and boundaries, useful in classifying surfaces, computing Betti numbers, and detecting holes in arbitrary dimensions. Higher homotopy groups capture detailed information about spaces' higher-dimensional loops and spheres, playing a crucial role in obstruction theory, fiber bundle classification, and stable homotopy theory. Applications in algebraic topology leverage homology for simpler invariants, while higher homotopy groups enable refined analysis of continuous deformations and homotopy types.
Connections to Other Mathematical Concepts
Homology groups provide algebraic invariants that classify topological spaces based on cycles and boundaries, directly connecting to chain complexes and algebraic topology. Higher homotopy groups generalize the fundamental group by capturing information about higher-dimensional spheres mapped into spaces, linking homotopy theory with category theory and fiber bundles. Both concepts intersect with spectral sequences and cohomology theories, deepening the understanding of space structure through algebraic methods.
Limitations and Challenges in Homology and Homotopy
Homology groups effectively capture information about the structure of spaces by associating algebraic invariants to topological features like holes and voids, but they often fail to detect finer, non-abelian structural properties present in more complex spaces. Higher homotopy groups provide deeper insights into the higher-dimensional "twists" and "loops" of spaces that homology overlooks, yet these groups are notoriously difficult to compute explicitly due to their non-abelian, intricate algebraic nature. Both homology and higher homotopy face challenges in computational complexity, with homology benefiting from robust algorithmic frameworks while higher homotopy requires advanced, often non-algorithmic, algebraic topological methods to analyze.
Summary: Choosing Between Homology and Higher Homotopy Groups
Homology groups provide an algebraic characterization of topological spaces by measuring cycles and boundaries, making them computationally accessible and widely applicable in classifying spaces. Higher homotopy groups capture more subtle and intricate features of spaces by describing equivalence classes of higher-dimensional spheres, but they are often complex to compute and interpret. Selecting between homology and higher homotopy groups depends on the balance between computational feasibility and the depth of geometric information required for the topological analysis.
Homology group Infographic
 libterm.com
libterm.com