Initial topology defines the coarsest topology on a set that makes a given family of functions continuous, ensuring minimal openness to preserve continuity. It plays a crucial role in various branches of mathematics, including functional analysis and topology, by providing a structured approach to understanding continuity through mappings. Explore the rest of the article to deepen your understanding of initial topology and its applications.
Table of Comparison
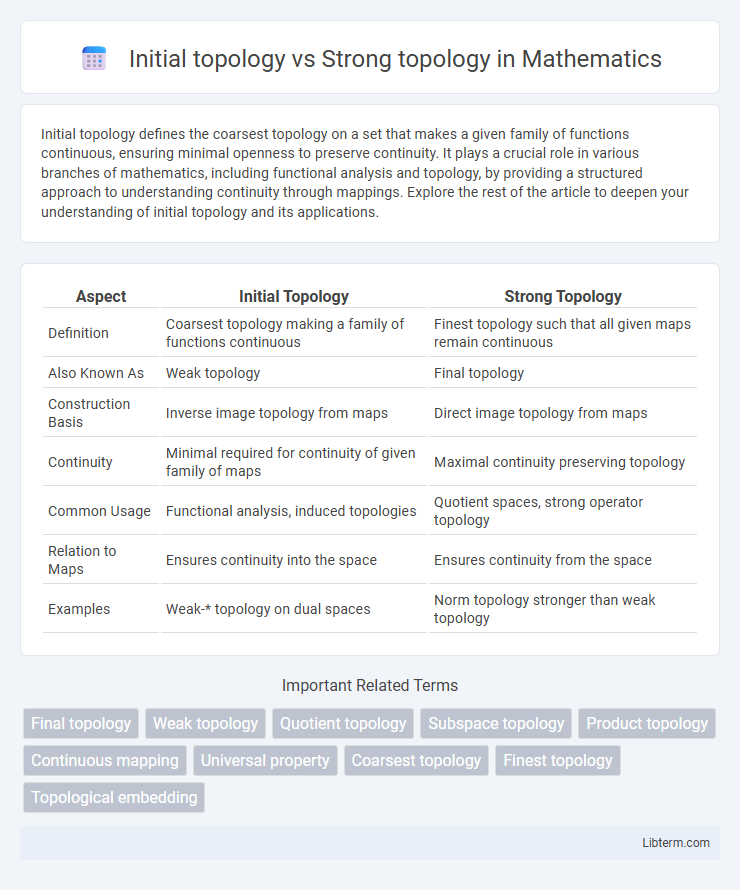
| Aspect | Initial Topology | Strong Topology |
|---|---|---|
| Definition | Coarsest topology making a family of functions continuous | Finest topology such that all given maps remain continuous |
| Also Known As | Weak topology | Final topology |
| Construction Basis | Inverse image topology from maps | Direct image topology from maps |
| Continuity | Minimal required for continuity of given family of maps | Maximal continuity preserving topology |
| Common Usage | Functional analysis, induced topologies | Quotient spaces, strong operator topology |
| Relation to Maps | Ensures continuity into the space | Ensures continuity from the space |
| Examples | Weak-* topology on dual spaces | Norm topology stronger than weak topology |
Introduction to Initial and Strong Topologies
Initial topology on a set X is defined as the coarsest topology making a given family of functions from X to topological spaces continuous, ensuring minimal open sets while preserving continuity. Strong topology, often known as the final or colimit topology, is the finest topology on a space Y that makes a given family of functions from topological spaces into Y continuous, maximizing open sets to maintain continuity. Understanding these dual concepts is fundamental in topology, influencing constructions in product spaces, quotient spaces, and functional analysis.
Defining Topological Spaces
Initial topology on a set \(X\) is defined relative to a family of functions \(\{ f_i : X \to Y_i \}\) to topological spaces \(\{Y_i\}\), making it the coarsest topology on \(X\) that renders all \(f_i\) continuous. Strong topology, often used in functional analysis, is the finest topology on a space \(X\) induced by a family of seminorms or maps, ensuring convergence properties are captured more robustly. While initial topology ensures minimal structural constraints for continuity, strong topology maximizes open sets to enhance convergence and functional properties.
What is the Initial Topology?
Initial topology is the coarsest topology on a set that makes a given family of functions from that set to topological spaces continuous. It is constructed by taking the preimages of open sets under these functions as the subbasis for the topology, ensuring minimal refinement. This contrasts with strong topology, which is generally finer, designed to facilitate convergence or continuity properties more robustly in function spaces.
Understanding the Strong Topology
The strong topology on a vector space is the finest locally convex topology that agrees with the dual pair under consideration, making all continuous linear functionals remain continuous. It is generated by a family of seminorms derived from bounded subsets of the dual space, ensuring convergence is closely tied to uniform convergence on these bounded sets. This contrasts with the initial topology, which is coarser and defined by the weakest topology that makes a given family of maps continuous, often leading to less stringent convergence criteria.
Constructing Initial vs Strong Topologies
Constructing initial topologies involves defining the coarsest topology on a set that makes a given family of functions continuous, ensuring minimal open sets while preserving continuity. In contrast, strong topologies are constructed as the finest topologies with respect to a family of continuous functions, maximizing open sets and convergence criteria. Initial and strong topologies serve dual purposes in topology, with initial topologies facilitating pullbacks and strong topologies enabling pushforwards in function spaces.
Key Differences Between Initial and Strong Topologies
Initial topology is defined as the coarsest topology making a given family of functions continuous, whereas strong topology is the finest topology that turns all mappings in a family continuous. The initial topology emphasizes minimal open sets to preserve continuity from target spaces, commonly used in product and subspace constructions. Strong topology, often appearing in functional analysis, refines open sets to capture stronger convergence properties, making it significantly finer than the initial topology.
Examples Illustrating Initial and Strong Topologies
The initial topology on a set X with respect to a family of functions {f_i : X - Y_i} is the coarsest topology making all f_i continuous, such as the weak* topology on the dual space of a normed vector space induced by evaluation maps. The strong topology on a function space, like the topology of uniform convergence on compact sets in C(X), results from a family of seminorms generating a finer topology than the initial topology derived from pointwise convergence. For instance, the initial topology on continuous functions C(X) induced by evaluation at points yields pointwise convergence, while the strong topology corresponds to uniform convergence, illustrating the difference in their generated open sets and convergence behavior.
Applications in Mathematical Analysis
Initial topology simplifies constructing topologies on function spaces, enabling continuity characterization through mappings from simpler spaces, essential in functional analysis and category theory. Strong topology, often defined by uniform convergence on bounded sets, equips spaces like duals of locally convex spaces with structures suitable for studying bounded linear operators and duality theory. These topologies optimize analysis in infinite-dimensional vector spaces, facilitating applications in operator theory and distribution theory.
Advantages and Limitations of Each Topology
Initial topology ensures the coarsest topology making a family of maps continuous, optimizing simplicity and minimal structure, advantageous for preserving continuity with fewer open sets but limited by its potential coarseness that may miss finer topological properties. Strong topology, formed as the finest topology combining given topologies, enhances convergence and separation properties, beneficial for detailed analysis and stronger continuity control, yet can become complex and overly fine, complicating direct application and computation. Selecting between initial and strong topology hinges on balancing the need for minimal continuity conditions versus richer structural detail in topological spaces.
Conclusion: Choosing the Right Topology
Selecting the appropriate topology depends on the desired continuity properties and the nature of the space in question; the initial topology ensures the coarsest topology making a family of functions continuous, ideal for preserving continuity while minimizing open sets. In contrast, the strong topology provides the finest topology generated by a family of seminorms, often used in functional analysis to facilitate convergence and completeness. Understanding these distinctions helps determine whether minimizing open sets (initial topology) or maximizing convergence properties (strong topology) better suits specific mathematical or applied problems.
Initial topology Infographic
 libterm.com
libterm.com