A principal bundle is a mathematical structure fundamental in differential geometry and gauge theory, consisting of a base space, a total space, and a continuous group action defining its fibers. Understanding its properties allows you to delve into connections, curvature, and symmetry in various physical and geometric contexts. Explore the remainder of this article to uncover how principal bundles shape modern geometry and physics.
Table of Comparison
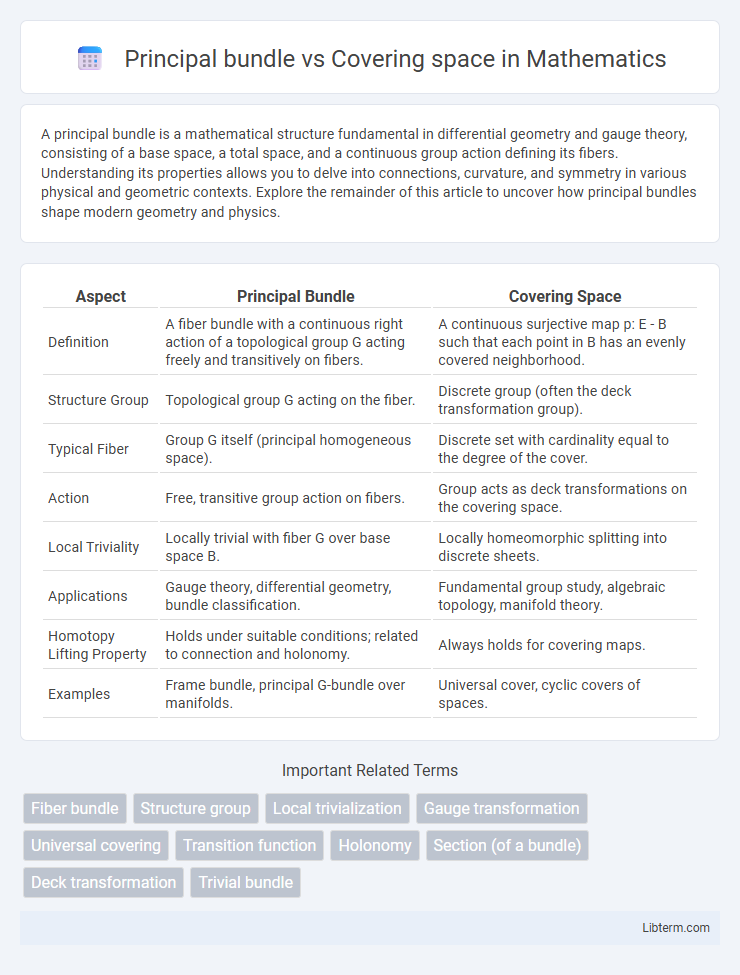
| Aspect | Principal Bundle | Covering Space |
|---|---|---|
| Definition | A fiber bundle with a continuous right action of a topological group G acting freely and transitively on fibers. | A continuous surjective map p: E - B such that each point in B has an evenly covered neighborhood. |
| Structure Group | Topological group G acting on the fiber. | Discrete group (often the deck transformation group). |
| Typical Fiber | Group G itself (principal homogeneous space). | Discrete set with cardinality equal to the degree of the cover. |
| Action | Free, transitive group action on fibers. | Group acts as deck transformations on the covering space. |
| Local Triviality | Locally trivial with fiber G over base space B. | Locally homeomorphic splitting into discrete sheets. |
| Applications | Gauge theory, differential geometry, bundle classification. | Fundamental group study, algebraic topology, manifold theory. |
| Homotopy Lifting Property | Holds under suitable conditions; related to connection and holonomy. | Always holds for covering maps. |
| Examples | Frame bundle, principal G-bundle over manifolds. | Universal cover, cyclic covers of spaces. |
Introduction to Principal Bundles and Covering Spaces
Principal bundles are mathematical structures consisting of a total space, a base space, and a continuous projection map equipped with a free and transitive action of a Lie group called the structure group, facilitating a geometric framework for fiber bundles with symmetry. Covering spaces involve a surjective continuous map from a covering space to a base space such that each point in the base space has an evenly covered neighborhood, providing a topological method to study spaces through simpler, locally homeomorphic copies. Both concepts play crucial roles in topology and geometry, with principal bundles emphasizing group actions and connections, while covering spaces focus on local homeomorphisms and lifting properties.
Mathematical Definitions
A principal bundle is a fiber bundle \( P \xrightarrow{\pi} M \) with a continuous right action by a topological group \( G \) that acts freely and transitively on each fiber, making the fibers homeomorphic to \( G \). A covering space \( \tilde{M} \xrightarrow{p} M \) is a continuous surjective map where each point in \( M \) has an open neighborhood evenly covered by disjoint homeomorphic slices of \( \tilde{M} \), ensuring local triviality with discrete fibers. Principal bundles generalize covering spaces by replacing the discrete fiber group with a possibly non-discrete Lie group, incorporating a richer geometric structure through the group action.
Structural Differences
Principal bundles involve a total space with a free and transitive action of a Lie group G, making the fibers isomorphic to G and allowing for a smooth group structure on the bundle. Covering spaces consist of a continuous surjective map with discrete fibers where locally the space is homeomorphic to a product of the base space and a discrete set, lacking a naturally defined group action. The key structural difference lies in principal bundles encoding symmetry through group actions, whereas covering spaces primarily capture topological unfolding without enforced algebraic structure.
Group Actions and Symmetries
Principal bundles and covering spaces both involve group actions that capture symmetries, but principal bundles feature a Lie group acting freely and transitively on each fiber, encoding continuous symmetries in geometric structures. Covering spaces are characterized by discrete group actions acting properly discontinuously, reflecting topological symmetries and often corresponding to the fundamental group's deck transformations. Understanding the distinction between continuous versus discrete group actions is crucial for classifying these spaces and analyzing their symmetry properties in differential geometry and topology.
Examples in Topology
A principal bundle, such as the Hopf fibration \(S^3 \to S^2\) with fiber \(S^1\), provides a framework where a Lie group acts freely and continuously on the total space, preserving the fiber structure. Covering spaces, exemplified by the universal cover \(\mathbb{R} \to S^1\), are special cases of fiber bundles with discrete fibers and locally homeomorphic projection maps. Unlike covering spaces that focus on discrete fiberings, principal bundles emphasize group actions and symmetries, serving as a fundamental tool in gauge theory and characteristic classes in topology.
Role in Fiber Bundle Theory
Principal bundles serve as a fundamental class of fiber bundles where the fiber is a Lie group acting freely and transitively on itself, enabling the construction of associated bundles with various fibers. Covering spaces represent fiber bundles with discrete fibers and play a crucial role in understanding topological properties and fundamental groups of base spaces. In fiber bundle theory, principal bundles facilitate the study of gauge theories and connections, while covering spaces provide insights into the global structure and classification of bundles.
Local Triviality Compared
A principal bundle and a covering space both exhibit local triviality, meaning they locally resemble a product of their base space with a typical fiber. Principal bundles have a structure group acting freely and transitively on each fiber, ensuring local trivializations compatible with the group's action. Covering spaces possess discrete fibers with local homeomorphisms to the base space, where local triviality reflects the existence of evenly covered neighborhoods but lacks the continuous group action characterizing principal bundles.
Applications in Mathematics and Physics
Principal bundles serve as a fundamental framework in gauge theory, facilitating the description of fiber bundles with group actions that model gauge fields in physics. Covering spaces, characterized by their role in algebraic topology, offer powerful tools for analyzing the fundamental group and solving lifting problems in complex manifolds. Both concepts intersect in the study of topological properties of fibered spaces, with principal bundles enabling the classification of gauge symmetries and covering spaces aiding in the characterization of topological invariants in mathematical physics.
Classification Results
Principal bundles over a topological space X are classified by homotopy classes of maps from X to the classifying space BG of the structure group G, encapsulating fiber bundle isomorphism classes in terms of homotopy theory. Covering spaces correspond to principal bundles with discrete groups as fibers, and their classification is given by the fundamental group p1(X), specifically via the correspondence between conjugacy classes of subgroups of p1(X) and equivalence classes of covering spaces. The classification of principal G-bundles relies on classifying maps to BG, whereas classification of covering spaces depends on algebraic properties of p1(X).
Summary of Key Distinctions
Principal bundles consist of a total space with a free action by a Lie group serving as the fiber, enabling a structured group symmetry, while covering spaces are local homeomorphisms where discrete fibers represent sheeted layers above the base space. Principal bundles feature continuous group actions preserving geometric or algebraic structures, often classified by characteristic classes, whereas covering spaces fundamentally characterize topological properties through lifting and monodromy. The conceptual divergence lies in principal bundles encoding symmetry via group actions with fiber structure, contrasting with covering spaces emphasizing local triviality and discrete multi-sheeted coverings without inherent group action.
Principal bundle Infographic
 libterm.com
libterm.com