Universal enveloping algebra provides a powerful framework to study Lie algebras by embedding them into associative algebras, enabling the use of algebraic tools for representation theory. This construction captures the structure and representations of Lie algebras while preserving their essential properties in a unified algebraic setting. Explore the article to understand how universal enveloping algebras can advance your grasp of Lie algebra theory.
Table of Comparison
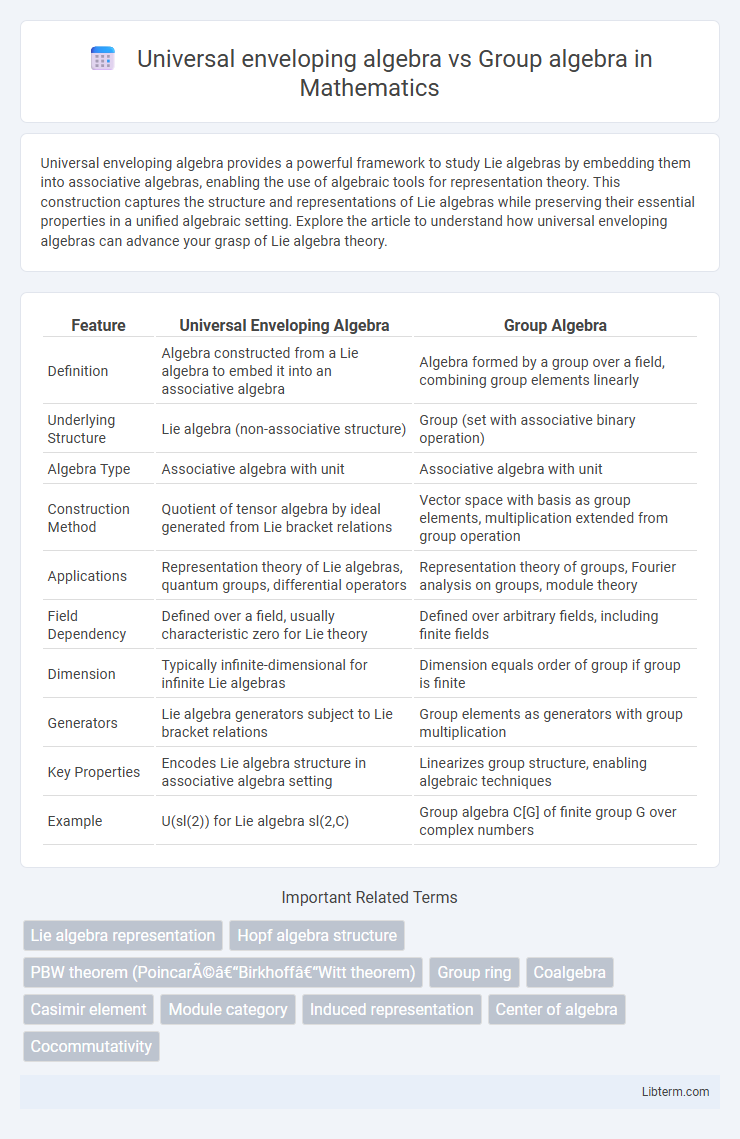
| Feature | Universal Enveloping Algebra | Group Algebra |
|---|---|---|
| Definition | Algebra constructed from a Lie algebra to embed it into an associative algebra | Algebra formed by a group over a field, combining group elements linearly |
| Underlying Structure | Lie algebra (non-associative structure) | Group (set with associative binary operation) |
| Algebra Type | Associative algebra with unit | Associative algebra with unit |
| Construction Method | Quotient of tensor algebra by ideal generated from Lie bracket relations | Vector space with basis as group elements, multiplication extended from group operation |
| Applications | Representation theory of Lie algebras, quantum groups, differential operators | Representation theory of groups, Fourier analysis on groups, module theory |
| Field Dependency | Defined over a field, usually characteristic zero for Lie theory | Defined over arbitrary fields, including finite fields |
| Dimension | Typically infinite-dimensional for infinite Lie algebras | Dimension equals order of group if group is finite |
| Generators | Lie algebra generators subject to Lie bracket relations | Group elements as generators with group multiplication |
| Key Properties | Encodes Lie algebra structure in associative algebra setting | Linearizes group structure, enabling algebraic techniques |
| Example | U(sl(2)) for Lie algebra sl(2,C) | Group algebra C[G] of finite group G over complex numbers |
Introduction to Universal Enveloping Algebra and Group Algebra
Universal enveloping algebra is a construction in Lie algebra theory that associates an associative algebra to a given Lie algebra, enabling the study of Lie algebra representations via module theory. Group algebra is an algebra formed from a group by extending its elements linearly over a field, providing a framework to analyze group representations and modules. Both structures serve as key tools in representation theory, with universal enveloping algebra capturing the Lie algebraic structure and group algebra encoding the discrete group symmetry.
Fundamental Definitions and Key Concepts
Universal enveloping algebra is an associative algebra constructed from a Lie algebra, capturing its Lie bracket through the commutator in an associative setting. Group algebra is a vector space formed from a group, with multiplication extending the group operation linearly, enabling representation theory of groups. Both algebras encode algebraic structures: universal enveloping algebra for Lie algebras and group algebra for discrete groups, facilitating module and representation analysis.
Algebraic Structures: Differences and Similarities
Universal enveloping algebras are constructed from Lie algebras to encode their Lie bracket structure within an associative algebra, while group algebras arise from groups by linearly extending the group multiplication to a vector space basis. Both structures form associative algebras over a field, yet universal enveloping algebras capture Lie algebra representations via the Poincare-Birkhoff-Witt theorem, whereas group algebras facilitate the study of group representations and modules. The key difference lies in their originating objects--Lie algebras versus groups--and how their respective multiplication rules are algebraically extended and preserved.
Universal Enveloping Algebra: Construction and Properties
The Universal Enveloping Algebra (UEA) of a Lie algebra is constructed as a quotient of the tensor algebra by the ideal generated by the Lie bracket relations, ensuring it captures the Lie algebra's structure within an associative algebra framework. Key properties include being a filtered algebra whose associated graded algebra is isomorphic to the symmetric algebra of the Lie algebra, enabling the PBW (Poincare-Birkhoff-Witt) theorem to hold. Unlike group algebras formed from groups, UEAs encode infinitesimal symmetries and provide a bridge between Lie algebras and representation theory through their universal mapping property.
Group Algebra: Construction and Properties
Group algebra is constructed by associating a vector space over a field with a given group, where the group elements form a basis and multiplication extends linearly from the group operation. This algebra encodes the group's structure and serves as a fundamental tool in representation theory, allowing group actions to be studied via linear transformations. Key properties include associativity, the existence of an identity element, and the ability to analyze modules and characters corresponding to the underlying group.
Representation Theory: Modules and Actions
Universal enveloping algebras serve as an essential tool to study representations of Lie algebras by providing a bridge between Lie algebra modules and associative algebra modules, enabling the use of module theory in representation analysis. Group algebras translate the abstract group elements into algebraic elements over a field, facilitating the investigation of group representations through modules over the group algebra. The action of the universal enveloping algebra on a module reflects the infinitesimal symmetry encoded by the Lie algebra, while the group algebra action captures the global symmetry of the group, allowing representation theory to explore continuous and discrete symmetries respectively.
Relationship to Lie Algebras and Groups
The universal enveloping algebra of a Lie algebra provides an associative algebra that encodes the Lie bracket structure, enabling the study of Lie algebra representations through module theory. In contrast, the group algebra of a group forms an associative algebra capturing the group's multiplicative structure, reflecting group elements as basis vectors. The universal enveloping algebra relates to Lie groups by serving as an algebraic bridge to their Lie algebras, while group algebras directly represent discrete group symmetries in an algebraic framework.
Applications in Mathematics and Physics
The universal enveloping algebra plays a crucial role in representation theory and Lie algebra applications, enabling the study of symmetries in differential equations and quantum mechanics. Group algebras facilitate the analysis of finite groups through module theory, impacting combinatorics, coding theory, and crystallography. Both structures provide foundational tools for understanding algebraic and geometric properties in theoretical physics and abstract algebra.
Comparative Advantages and Use Cases
Universal enveloping algebras provide a powerful framework for studying Lie algebras by capturing their non-associative structure within an associative algebra, facilitating representation theory and differential operators analysis. Group algebras, constructed from groups over fields, excel in encoding group symmetries and are essential in character theory, finite group representations, and Fourier analysis on groups. While universal enveloping algebras are crucial for Lie algebra representations and quantum mechanics applications, group algebras find extensive use in combinatorics, group theory, and harmonic analysis, highlighting their complementary roles in algebraic structures.
Summary Table: Universal Enveloping Algebra vs Group Algebra
The Universal Enveloping Algebra (UEA) of a Lie algebra encodes its structure in an associative algebra, allowing representation theory and deformation analysis, while the Group Algebra forms from a group by extending scalars to a field, capturing group symmetries algebraically. Key differences include UEA's reliance on Lie bracket relations versus group algebra's basis elements indexed by group members, and the UEA's role in Lie algebra representations versus the group algebra's facilitation of group representation theory. The summary table highlights distinctions in construction, algebraic relations, basis, and applications, showcasing UEA as a tool for Lie algebra analysis and group algebra for finite group symmetry representations.
Universal enveloping algebra Infographic
 libterm.com
libterm.com