Direct sum is a fundamental concept in linear algebra and abstract algebra, representing the combination of two subspaces or modules into a larger space where each element can be uniquely expressed as a sum of elements from the original spaces. This operation is crucial for understanding vector space decompositions and simplifying complex algebraic structures. Explore the rest of the article to deepen your understanding of direct sums and their applications.
Table of Comparison
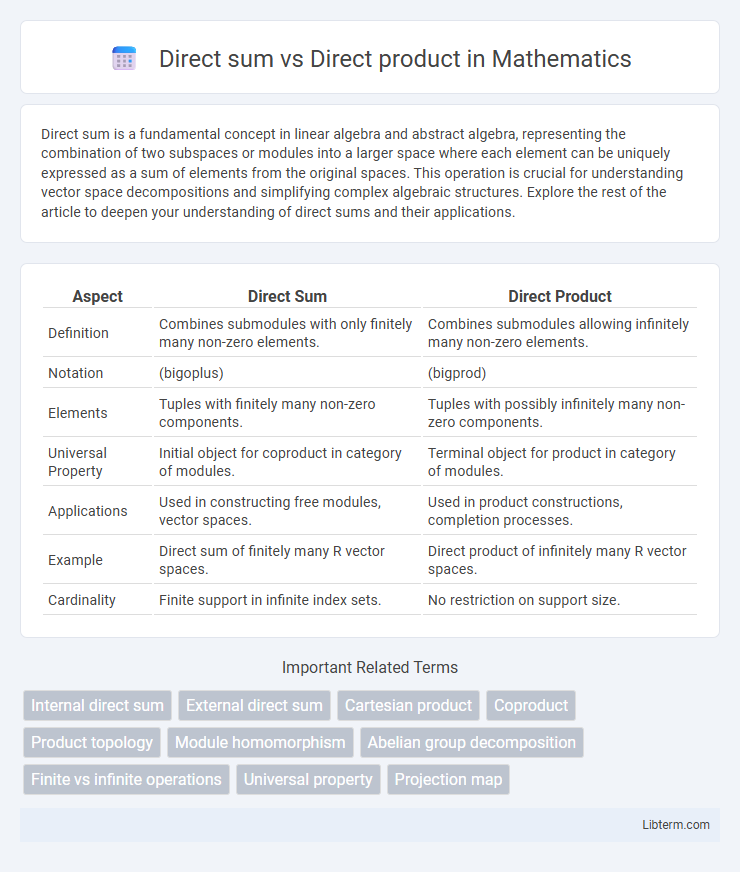
| Aspect | Direct Sum | Direct Product |
|---|---|---|
| Definition | Combines submodules with only finitely many non-zero elements. | Combines submodules allowing infinitely many non-zero elements. |
| Notation | (bigoplus) | (bigprod) |
| Elements | Tuples with finitely many non-zero components. | Tuples with possibly infinitely many non-zero components. |
| Universal Property | Initial object for coproduct in category of modules. | Terminal object for product in category of modules. |
| Applications | Used in constructing free modules, vector spaces. | Used in product constructions, completion processes. |
| Example | Direct sum of finitely many R vector spaces. | Direct product of infinitely many R vector spaces. |
| Cardinality | Finite support in infinite index sets. | No restriction on support size. |
Introduction to Direct Sum and Direct Product
The direct sum of a family of modules or vector spaces consists of elements with finitely many nonzero components, enabling a structure that simplifies decomposition and analysis. In contrast, the direct product includes all possible tuples without restriction on the number of nonzero components, allowing for a more extensive and less constrained construction. These concepts are fundamental in algebra and functional analysis, providing different approaches to combining structures while preserving internal operations.
Definitions: Direct Sum Explained
The direct sum of a family of modules or vector spaces is the set of tuples with finite nonzero entries, forming a submodule of the direct product. Elements in the direct sum have only finitely many components different from the zero element, ensuring a well-defined structure suitable for algebraic operations. This contrasts with the direct product, which allows infinitely many nonzero components, making the direct sum a more restrictive but algebraically significant construction.
Understanding Direct Product
The direct product of a family of groups is the set of all tuples formed by selecting an element from each group, equipped with component-wise group operations, allowing infinite collections without restriction. Unlike the direct sum, which requires all but finitely many elements to be the identity, the direct product includes every possible combination, making it a more comprehensive construction useful in algebraic topology and module theory. Understanding the distinction clarifies how infinite products maintain structure and enable extensions beyond finitely supported elements.
Key Differences Between Direct Sum and Direct Product
The direct sum and direct product distinguish in their handling of component collections: the direct sum combines elements with only finitely many nonzero entries, while the direct product allows infinitely many nonzero components. In algebraic structures like modules or vector spaces, the direct sum forms a substructure of the direct product, emphasizing finite linear combinations versus unrestricted tuples. Topologically, the direct product inherits the product topology, often resulting in a more complex space than the direct sum, which carries a coarser topology tied to finite support.
Applications in Algebra and Linear Algebra
Direct sums enable the decomposition of vector spaces or modules into simpler, independent substructures, facilitating dimension counting and structural analysis in linear algebra and module theory. Direct products, contrastingly, allow the construction of larger algebraic objects incorporating all components while preserving their individual operations, crucial in category theory and the study of infinite product structures. Applications in algebra often leverage direct sums for simplifying representation theory and homological algebra problems, whereas direct products are essential for dealing with infinite-dimensional spaces and constructing product topologies in functional analysis.
Properties of Direct Sum
The direct sum of modules or vector spaces involves combining elements such that each component is nonzero in only finitely many positions, ensuring a well-defined algebraic structure with simpler computations and clearer submodule characterization. It preserves exact sequences and is inherently related to coproducts in category theory, making it crucial for decomposing modules into simpler, manageable parts. In contrast to the direct product, the direct sum allows homomorphisms to act componentwise without convergence concerns, facilitating its application in functional analysis and module theory.
Properties of Direct Product
The direct product of a family of groups forms a group where each element is an ordered tuple combining elements from each component group, with group operations performed component-wise. It satisfies universal properties characterized by projection homomorphisms onto each factor, making it a categorical product in the category of groups. Unlike the direct sum, the direct product includes all possible tuples, leading to a generally larger and more complex structure, especially in infinite cases where all factor groups contribute without restriction.
Direct Sum and Direct Product in Group Theory
In group theory, the direct sum of groups is a subgroup of the direct product where all but finitely many components are the identity element, enabling the construction of groups with finitely supported tuples. The direct product, by contrast, includes all tuples of elements from each group without restriction, resulting in a potentially larger group structure. Direct sums are particularly critical in the study of abelian groups and module theory due to their finite support condition, which affects homomorphisms and subgroup analysis.
Visualizing Direct Sum vs Direct Product
Visualizing direct sum involves representing vectors as ordered pairs or tuples where each component belongs to a corresponding subspace, emphasizing disjointness and independence. The direct product portrays elements as all possible combinations of component vectors, highlighting a broader structure that includes shared dimensions. Graphically, direct sums appear as separate axes forming a coordinate grid, while direct products resemble a multidimensional space containing overlapping features from each factor.
Summary and Key Takeaways
Direct sum and direct product differ primarily in the scope of their elements: direct sum consists of tuples with finitely many nonzero components, while direct product allows infinitely many nonzero components. In algebraic structures such as groups or vector spaces, the direct sum is a subgroup of the direct product, highlighting a key structural distinction. The choice between using direct sum or direct product impacts convergence, topology, and computational complexity in applications across mathematics and physics.
Direct sum Infographic
 libterm.com
libterm.com