The Hankel transform is an integral transform used primarily in solving problems with cylindrical symmetry in physics and engineering. It is closely related to the Fourier transform but operates on functions defined over radial distances, making it essential for analyzing wave propagation and heat conduction in circular domains. Explore the article to deepen your understanding of how the Hankel transform can be applied to your scientific and engineering challenges.
Table of Comparison
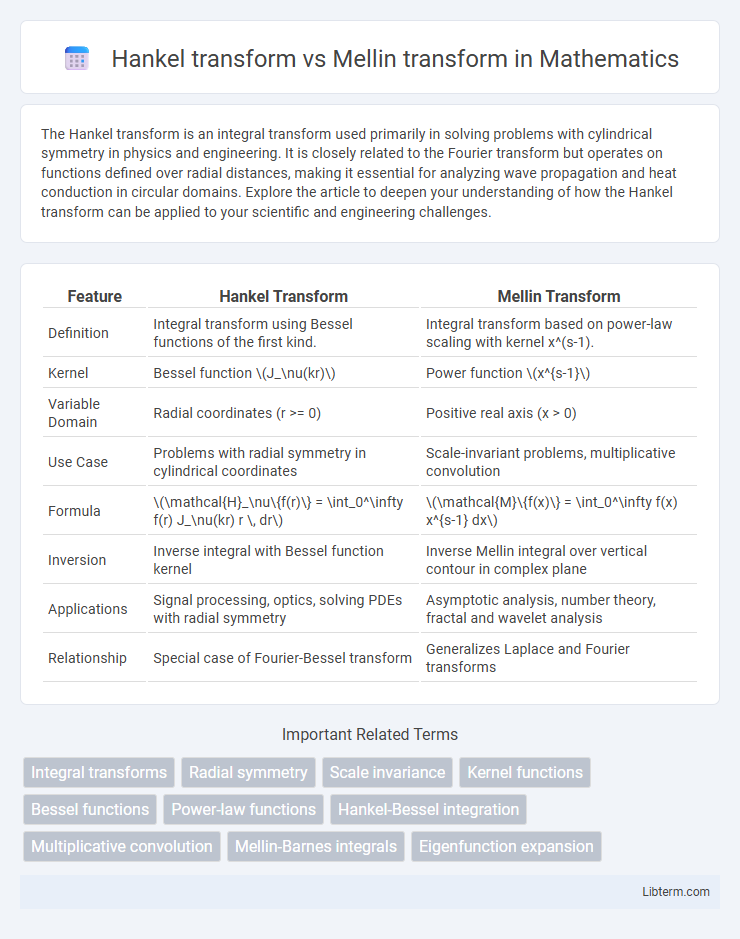
| Feature | Hankel Transform | Mellin Transform |
|---|---|---|
| Definition | Integral transform using Bessel functions of the first kind. | Integral transform based on power-law scaling with kernel x^(s-1). |
| Kernel | Bessel function \(J_\nu(kr)\) | Power function \(x^{s-1}\) |
| Variable Domain | Radial coordinates (r >= 0) | Positive real axis (x > 0) |
| Use Case | Problems with radial symmetry in cylindrical coordinates | Scale-invariant problems, multiplicative convolution |
| Formula | \(\mathcal{H}_\nu\{f(r)\} = \int_0^\infty f(r) J_\nu(kr) r \, dr\) | \(\mathcal{M}\{f(x)\} = \int_0^\infty f(x) x^{s-1} dx\) |
| Inversion | Inverse integral with Bessel function kernel | Inverse Mellin integral over vertical contour in complex plane |
| Applications | Signal processing, optics, solving PDEs with radial symmetry | Asymptotic analysis, number theory, fractal and wavelet analysis |
| Relationship | Special case of Fourier-Bessel transform | Generalizes Laplace and Fourier transforms |
Introduction to Integral Transforms
The Hankel transform and Mellin transform are integral transforms widely used in mathematical physics and engineering for solving differential equations and analyzing functions. The Hankel transform is specifically suited for problems with cylindrical symmetry, utilizing Bessel functions as kernels to convert functions defined on the positive real axis. The Mellin transform, involving complex power functions, is effective for scale-invariant problems and asymptotic analysis, providing a powerful tool for multiplicative convolution and inverse Laplace transform relations.
Overview of the Hankel Transform
The Hankel transform is an integral transform widely used in solving problems with cylindrical symmetry, especially in physics and engineering. It involves Bessel functions of the first kind as kernels, mapping a function into a domain that simplifies radial differential equations. This transform contrasts with the Mellin transform, which is effective for scale-invariant problems and uses power-law kernels, making the Hankel transform specifically suited for analyzing circular or cylindrical geometries.
Overview of the Mellin Transform
The Mellin transform is an integral transform that converts a function into a complex frequency domain, characterized by its ability to analyze multiplicative scaling properties and is widely used in number theory, fractal analysis, and solving differential equations with scale invariance. Unlike the Hankel transform, which operates on radial functions and leverages Bessel functions for problems with circular symmetry, the Mellin transform is defined by integrating a function multiplied by a power function over the positive real axis. This transform provides a powerful framework for scaling analysis and asymptotic expansions, making it essential in image processing, wavelet theory, and complex variable applications.
Mathematical Definitions and Formulations
The Hankel transform is defined as an integral transform involving Bessel functions of the first kind \( J_\nu \), specifically \(\mathcal{H}_\nu\{f(r)\} = \int_0^\infty f(r) J_\nu(kr) r \, dr \), widely used in solving radial problems in cylindrical coordinates. The Mellin transform is formulated as \(\mathcal{M}\{f(x)\}(s) = \int_0^\infty x^{s-1} f(x) \, dx\), converting functions into complex frequency space, often applied in scale-invariant analysis. Both transforms serve distinct purposes: the Hankel transform addresses circular symmetry with order \(\nu\) Bessel functions, while the Mellin transform handles multiplicative scaling via complex powers \( s \).
Key Properties and Theorems
The Hankel transform is characterized by its radial symmetry and is integral in solving problems with cylindrical coordinates, using Bessel functions as kernels, which exhibit orthogonality and inversion properties critical for signal processing and differential equations. The Mellin transform features scale-invariance and converts multiplicative convolutions into additive ones, making it particularly effective for analyzing asymptotic behaviors and fractal structures, supported by the Mellin inversion theorem and Parseval-type identities. Both transforms leverage integral kernel functions to facilitate the transformation of functions into different domains for simplified analysis but differ fundamentally in their application contexts and functional symmetries.
Applications in Signal and Image Processing
The Hankel transform is primarily utilized in circularly symmetric signal and image processing tasks such as wave propagation analysis and radially symmetric pattern recognition. The Mellin transform excels in scale-invariant feature extraction, enabling robust image scaling, texture analysis, and pattern matching across varying resolutions. Both transforms enhance signal processing by providing domain-specific tools for handling symmetry and scale variations in complex data sets.
Differences in Domains and Use-Cases
The Hankel transform primarily operates on functions defined over radial distances in two-dimensional spaces, making it ideal for problems involving circular symmetry such as wave propagation and heat conduction. The Mellin transform acts on functions defined over positive real numbers and is often used in scale-invariant analysis, including applications in fractals, number theory, and asymptotic expansions. The distinct domains reflect their use-cases: Hankel transform suits radial function analysis in cylindrical coordinates, while Mellin transform excels in multiplicative scaling problems.
Computational Considerations
The Hankel transform is computationally efficient for radially symmetric functions due to its reliance on Bessel functions and can be discretized using fast algorithms like the Fast Hankel Transform. The Mellin transform, suited for scale-invariant problems, requires careful numerical integration often involving contour deformation to handle complex variables, which can increase computational complexity. Both transforms benefit from specialized numerical methods, but the Hankel transform generally offers faster computation in applications with circular symmetry.
Advantages and Limitations of Each Transform
The Hankel transform excels in analyzing radially symmetric functions and solving differential equations in cylindrical coordinates, offering efficient computation for problems involving Bessel functions; however, it is limited to functions defined on non-negative real domains and may be less effective for non-radial data. The Mellin transform provides powerful scale-invariant analysis, beneficial in multiplicative convolution and asymptotic analysis, and supports complex variable techniques, yet it struggles with functions not well-behaved under scaling and may require careful contour integration to handle singularities. Both transforms serve distinct applications with the Hankel transform prioritizing spatial radial symmetry and the Mellin transform focusing on scale properties, limiting their interchangeability in signal processing or applied mathematics.
Choosing Between Hankel and Mellin Transforms
Choosing between Hankel and Mellin transforms depends on the problem's symmetry and domain. The Hankel transform is ideal for radially symmetric functions in cylindrical coordinates, leveraging Bessel functions to simplify integral equations. In contrast, the Mellin transform excels in scale-invariant problems by converting multiplicative convolution into algebraic multiplication, making it suitable for analyzing asymptotic behaviors and power-law distributions.
Hankel transform Infographic
 libterm.com
libterm.com