A factor group, also known as a quotient group, is formed by partitioning a group into cosets of a normal subgroup and defining a group operation on these cosets. This construction plays a crucial role in group theory by simplifying complex groups into more manageable structures while preserving group properties. Explore the full article to deepen your understanding of factor groups and their applications in abstract algebra.
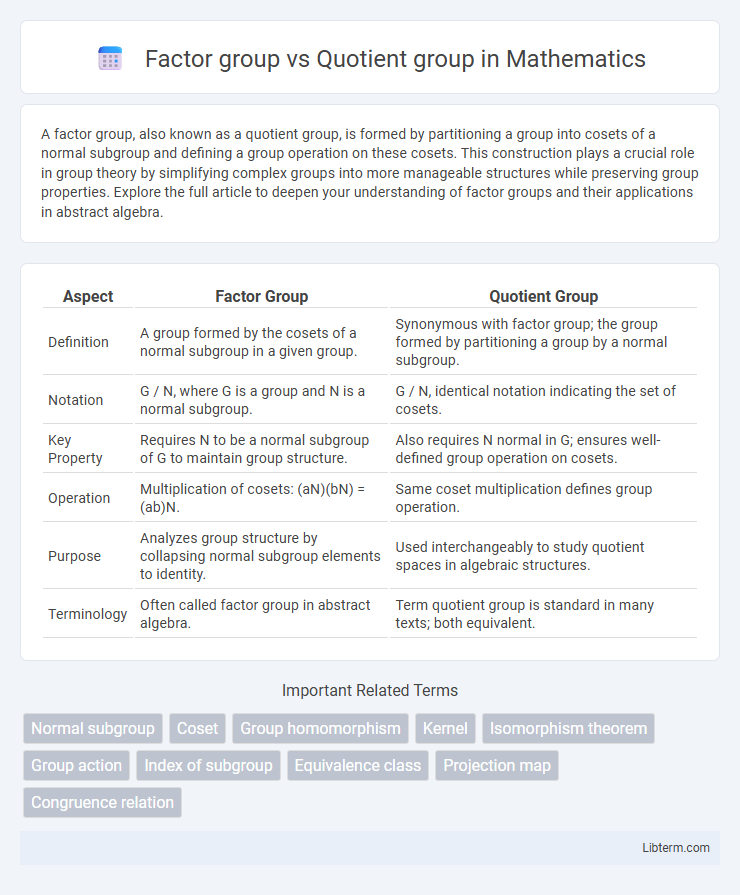
Table of Comparison
| Aspect | Factor Group | Quotient Group |
|---|---|---|
| Definition | A group formed by the cosets of a normal subgroup in a given group. | Synonymous with factor group; the group formed by partitioning a group by a normal subgroup. |
| Notation | G / N, where G is a group and N is a normal subgroup. | G / N, identical notation indicating the set of cosets. |
| Key Property | Requires N to be a normal subgroup of G to maintain group structure. | Also requires N normal in G; ensures well-defined group operation on cosets. |
| Operation | Multiplication of cosets: (aN)(bN) = (ab)N. | Same coset multiplication defines group operation. |
| Purpose | Analyzes group structure by collapsing normal subgroup elements to identity. | Used interchangeably to study quotient spaces in algebraic structures. |
| Terminology | Often called factor group in abstract algebra. | Term quotient group is standard in many texts; both equivalent. |
Introduction to Factor Groups and Quotient Groups
Factor groups and quotient groups both refer to the construction of new groups by partitioning an original group G using a normal subgroup N. The quotient group G/N consists of cosets of N in G, where each coset represents an equivalence class under the relation defined by N. These structures allow algebraists to analyze group properties by studying simpler groups derived from complex ones, with applications in many areas such as algebraic topology and Galois theory.
Defining Groups and Subgroups
A factor group, or quotient group, is formed by partitioning a group \(G\) into cosets of a normal subgroup \(N \triangleleft G\), where the set of these cosets inherits a group structure under well-defined multiplication. Defining the factor group \(G/N\) requires the subgroup \(N\) to be normal so that the operation \((aN)(bN) = (ab)N\) is consistent and independent of representatives. This construction contrasts with general subgroup definitions, where normality is not required, highlighting the importance of normal subgroups in forming quotient groups.
What is a Factor Group?
A factor group, also known as a quotient group, is formed by partitioning a group \( G \) into cosets of a normal subgroup \( N \). The elements of the factor group \( G/N \) are these cosets, which combine under the group operation induced by \( G \). This construction simplifies the study of group properties by analyzing the structure of \( G \) relative to \( N \).
What is a Quotient Group?
A quotient group, also known as a factor group, is formed by dividing a group \(G\) by one of its normal subgroups \(N\), denoted as \(G/N\). The elements of the quotient group are the cosets of \(N\) in \(G\), and the group operation is defined by the multiplication of these cosets. Quotient groups play a critical role in group theory, facilitating the analysis of group structure through homomorphisms and the First Isomorphism Theorem.
Relationship Between Factor Group and Quotient Group
A factor group and a quotient group are essentially the same concept in group theory, representing the set of cosets of a normal subgroup within a group. The relationship between them lies in their interchangeable terminology, where "factor group" emphasizes the role of partitioning by a normal subgroup, while "quotient group" highlights the algebraic structure obtained by this partitioning. Both terms denote the group formed by elements of the original group modulo the normal subgroup, preserving group operations in the reduced structure.
Notation and Terminology Differences
Factor groups and quotient groups refer to the same algebraic structure formed by partitioning a group G by a normal subgroup N, commonly denoted as G/N. The term "factor group" is traditionally used in older literature, while "quotient group" is the preferred modern terminology in abstract algebra. Notation remains consistent, with both representing the set of cosets of N in G under the operation induced by G, but "quotient" emphasizes the partitioning and equivalence relation aspect.
Constructing Factor (Quotient) Groups
Constructing factor groups involves partitioning a group \(G\) by a normal subgroup \(N\), where the elements of the factor group \(G/N\) are the cosets of \(N\) in \(G\). The operation on \(G/N\) is defined by multiplying cosets: \((aN)(bN) = (ab)N\), ensuring the group structure is preserved due to the normality of \(N\). This construction enables the study of group properties through simpler quotient structures, facilitating analysis via homomorphisms and the isomorphism theorems.
Examples: Factor Groups vs Quotient Groups
Factor groups and quotient groups are interchangeable terms in group theory, both referring to the set of cosets of a normal subgroup. For example, the factor group \( \mathbb{Z}/n\mathbb{Z} \) consists of integers modulo \( n \), derived by partitioning the group of integers \( \mathbb{Z} \) with the subgroup \( n\mathbb{Z} \). Another instance is the quotient group \( S_3 / A_3 \), where the symmetric group \( S_3 \) is factored by its normal subgroup \( A_3 \), resulting in a group isomorphic to \( \mathbb{Z}_2 \).
Applications in Group Theory
Factor groups, also known as quotient groups, are fundamental in studying group homomorphisms and normal subgroups, enabling the simplification of complex groups into more manageable structures. They play a crucial role in classifying groups via the First Isomorphism Theorem and in analyzing symmetry within algebraic systems. Applications include solving polynomial equations through Galois theory and exploring group actions in geometry and topology.
Summary: Key Differences and Similarities
Factor groups and quotient groups refer to the same mathematical concept where a group G is partitioned by a normal subgroup N, forming the set of cosets G/N. Both terms emphasize the structure of the resulting group, inheriting operation properties from G and simplifying complex group analysis. Key differences lie mainly in terminology preference across texts, while similarities include the fundamental idea of constructing new groups through equivalence classes derived from normal subgroups.
Factor group Infographic
 libterm.com
libterm.com