A surjective function, also known as onto, maps every element in the codomain to at least one element in the domain, ensuring full coverage of the target set. Understanding surjectivity is essential in fields like mathematics and computer science for solving equations and modeling relationships effectively. Explore the rest of this article to deepen your grasp of surjective functions and their practical applications.
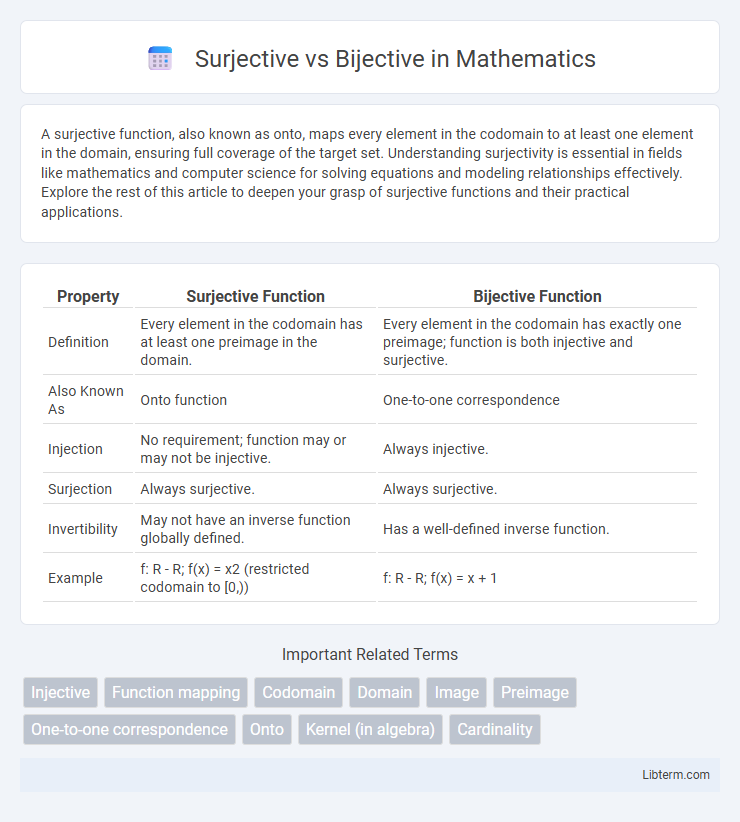
Table of Comparison
| Property | Surjective Function | Bijective Function |
|---|---|---|
| Definition | Every element in the codomain has at least one preimage in the domain. | Every element in the codomain has exactly one preimage; function is both injective and surjective. |
| Also Known As | Onto function | One-to-one correspondence |
| Injection | No requirement; function may or may not be injective. | Always injective. |
| Surjection | Always surjective. | Always surjective. |
| Invertibility | May not have an inverse function globally defined. | Has a well-defined inverse function. |
| Example | f: R - R; f(x) = x2 (restricted codomain to [0,)) | f: R - R; f(x) = x + 1 |
Understanding Functions: Key Concepts
Surjective functions map every element of the codomain to at least one element in the domain, ensuring full coverage of the output set, which is essential for solving equations and defining inverse functions on the codomain. Bijective functions are both injective (one-to-one) and surjective (onto), establishing a perfect pairing between domain and codomain elements, enabling the existence of a two-sided inverse function. Understanding the distinction between surjective and bijective functions is crucial for analyzing mappings, constructing inverses, and exploring isomorphisms in advanced mathematics.
What is a Surjective (Onto) Function?
A surjective (onto) function is defined by its property that every element in the function's codomain has at least one corresponding element in its domain mapping to it, ensuring full coverage of the codomain. Surjectivity guarantees that the range of the function is equal to its codomain, which is critical in solving equations and establishing existence in functional analysis. Unlike bijective functions, surjections do not require uniqueness of mappings, only that the entire codomain is reached by the function.
What is a Bijective Function?
A bijective function is a type of mapping where every element in the domain corresponds to a unique element in the codomain, ensuring a one-to-one and onto relationship. This means the function is both injective (no two domain elements map to the same codomain element) and surjective (every element in the codomain is mapped by some element in the domain). Bijective functions guarantee an exact pairing, allowing the existence of an inverse function that reverses the mapping perfectly.
Surjective vs Bijective: Core Differences
Surjective functions map every element of the codomain to at least one element of the domain, ensuring full coverage of the codomain. Bijective functions are both surjective and injective, meaning they establish a perfect one-to-one correspondence between domain and codomain elements. The core difference lies in bijections requiring uniqueness of mapping, while surjections only require completeness of range coverage.
Visualizing Surjective and Bijective Functions
Visualizing surjective functions involves mapping elements of the domain onto every element in the codomain, ensuring full coverage without gaps. Bijective functions can be depicted as one-to-one correspondences where each element in the domain pairs uniquely with one in the codomain, creating a perfect matchup. Diagrams for surjective functions show arrows covering all codomain points, while bijections illustrate both surjectivity and injectivity with exclusive, complete pairings.
Mathematical Notation and Definitions
A function \( f: A \to B \) is surjective (onto) if for every \( b \in B \), there exists at least one \( a \in A \) such that \( f(a) = b \), symbolically \( \forall b \in B, \exists a \in A : f(a) = b \). A bijective function is both injective and surjective, meaning \( f: A \to B \) satisfies \( \forall b \in B, \exists! a \in A : f(a) = b \), where \( \exists! \) denotes the existence of a unique element. Bijective functions admit an inverse \( f^{-1}: B \to A \) such that \( f^{-1}(f(a)) = a \) and \( f(f^{-1}(b)) = b \).
Practical Applications in Mathematics
Surjective functions ensure every element in the codomain is mapped by at least one element from the domain, crucial in solving equations and modeling real-world problems like resource allocation. Bijective functions establish one-to-one correspondences, enabling invertibility which underpins cryptography, data encoding, and permutation group theory. In linear algebra, bijections correspond to invertible matrices, facilitating transformations and solving systems of linear equations efficiently.
Common Examples of Surjective and Bijective Functions
Surjective functions are exemplified by the projection map from \(\mathbb{R}^2\) to \(\mathbb{R}\), where every real number corresponds to at least one point in the plane. Bijective functions include the exponential function \(f:\mathbb{R} \to (0, \infty)\), which is both one-to-one and onto, establishing a perfect pairing between domain and codomain. The identity function on any set is a classical bijection, serving as a fundamental example in mathematical analysis and algebra.
Importance in Algebra and Set Theory
Surjective functions ensure every element in the codomain is mapped by at least one element in the domain, making them essential for establishing onto mappings in algebra and set theory. Bijective functions, combining both injective and surjective properties, create one-to-one correspondences crucial for defining isomorphisms between algebraic structures and establishing equivalences between sets. Understanding surjective and bijective functions enables the precise characterization of function properties needed for transformations, homomorphisms, and cardinality comparisons in mathematical analysis.
Summary: Choosing Between Surjective and Bijective Functions
Surjective functions map every element of the codomain to at least one element of the domain, ensuring full coverage but allowing multiple inputs to correspond to the same output. Bijective functions provide a one-to-one correspondence between domain and codomain, guaranteeing both surjectivity and injectivity, which enables invertibility. Selecting between surjective and bijective functions depends on whether invertible mappings or comprehensive output coverage is the priority in applications like encoding or function transformations.
Surjective Infographic
 libterm.com
libterm.com