A uniform submodule is a nonzero module in which every pair of nonzero submodules intersects nontrivially, ensuring the submodule is indecomposable in a strong sense. This concept plays a crucial role in module theory and the study of module decompositions, particularly within the context of uniform dimension and essential extensions. Explore the rest of the article to deepen your understanding of uniform submodules and their applications in algebra.
Table of Comparison
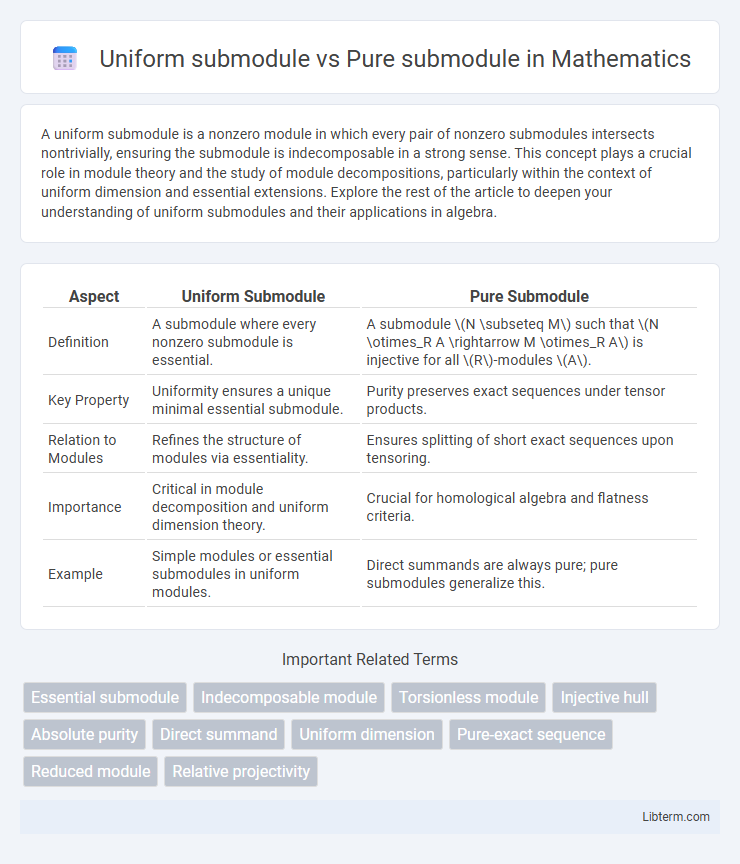
| Aspect | Uniform Submodule | Pure Submodule |
|---|---|---|
| Definition | A submodule where every nonzero submodule is essential. | A submodule \(N \subseteq M\) such that \(N \otimes_R A \rightarrow M \otimes_R A\) is injective for all \(R\)-modules \(A\). |
| Key Property | Uniformity ensures a unique minimal essential submodule. | Purity preserves exact sequences under tensor products. |
| Relation to Modules | Refines the structure of modules via essentiality. | Ensures splitting of short exact sequences upon tensoring. |
| Importance | Critical in module decomposition and uniform dimension theory. | Crucial for homological algebra and flatness criteria. |
| Example | Simple modules or essential submodules in uniform modules. | Direct summands are always pure; pure submodules generalize this. |
Introduction to Submodules in Module Theory
Uniform submodules are submodules in which every pair of nonzero submodules has a nonzero intersection, highlighting their highly interconnected structure within module theory. Pure submodules maintain the property that their inclusion preserves exact sequences after tensoring with any module, emphasizing their significance in preserving module homological properties. Understanding the distinction between uniform and pure submodules is essential for analyzing module decomposition and purity in algebraic structures.
Defining Uniform Submodules
A uniform submodule is defined as a submodule in which every pair of nonzero submodules has a nonzero intersection, ensuring indivisibility within its structure. This concept contrasts with pure submodules, which maintain exact sequences under tensoring with any module, emphasizing structural stability rather than uniformity. Understanding uniform submodules involves analyzing their role in module theory as building blocks that resist decomposition into smaller, non-intersecting parts.
Defining Pure Submodules
Pure submodules are defined as submodules \( N \) of a module \( M \) such that the tensor product with any module preserves exact sequences, meaning the inclusion \( N \hookrightarrow M \) remains injective after tensoring with any \( R \)-module. Uniform submodules, in contrast, focus on intersections of nonzero submodules being nonzero, emphasizing structural indivisibility rather than tensor product behavior. Defining pure submodules involves ensuring that for every finite system of linear equations solvable in \( M \), solutions exist within \( N \), capturing algebraic purity in module theory.
Structural Differences between Uniform and Pure Submodules
Uniform submodules are characterized by the property that every nonzero submodule intersects nontrivially, creating an indecomposable structure focused on uniformity of intersections. Pure submodules maintain a structural integrity by preserving exact sequences under tensor products, ensuring that systems of linear equations solvable in the larger module remain solvable within the submodule. The key structural difference lies in uniform submodules emphasizing internal intersections and indecomposability, whereas pure submodules focus on preservation of algebraic properties through exactness under tensoring.
Key Properties of Uniform Submodules
Uniform submodules exhibit a key property where every nonzero submodule intersects nontrivially, ensuring a strong form of indecomposability crucial for module theory. These submodules play a vital role in understanding the decomposition of modules into uniform components, directly contributing to the Krull-Schmidt theorem. In contrast, pure submodules maintain exactness upon tensoring, which preserves structural properties but does not guarantee the intersection characteristics central to uniform submodules.
Key Properties of Pure Submodules
Pure submodules preserve exact sequences when tensored with any module, ensuring that the inclusion map remains injective under tensor operations. They are characterized by the property that every finite system of linear equations solvable in the larger module is also solvable within the pure submodule. Unlike uniform submodules, which are defined by their uniformity in having all nonzero submodules intersect nontrivially, pure submodules emphasize tensorial exactness and closure properties critical in homological algebra.
Examples Illustrating Uniform and Pure Submodules
A uniform submodule is exemplified by a simple module, such as a cyclic submodule generated by an element with no nontrivial submodules, like the submodule \( \mathbb{Z}/p\mathbb{Z} \) in a \( \mathbb{Z} \)-module over a prime \( p \). Pure submodules include examples such as direct summands and submodules where the tensor product with any module preserves exact sequences, like \( p\mathbb{Z} \) as a pure submodule of \( \mathbb{Z} \). The distinction is clear in modules over rings like \( \mathbb{Z} \), where uniformity relates to submodules with minimal nonzero intersections, and purity ensures compatibility with tensor operations reflecting the module's intrinsic structure.
Homological Implications in Module Theory
Uniform submodules exhibit essentiality in homological contexts by ensuring that every nonzero submodule intersects nontrivially, leading to indecomposability properties crucial for constructing injective envelopes. Pure submodules maintain exactness under tensoring, which preserves flatness and projectivity conditions pivotal for derived functor calculations such as Tor and Ext. The distinction influences resolutions in homological algebra, where uniform submodules aid in minimal injective resolutions, while pure submodules facilitate control over splitting properties and purity in short exact sequences.
Applications and Use Cases
Uniform submodules are essential in module theory for analyzing decompositions where every nonzero submodule is essential, making them valuable in the study of indecomposable modules and representation theory. Pure submodules are crucial in applications involving exact sequences and homological algebra, especially in contexts where preservation of tensor products and flatness conditions are required. In algebraic geometry and model theory, pure submodules facilitate the study of definable sets and allow control over structural properties during localization and base changes.
Summary: Comparing Uniform and Pure Submodules
Uniform submodules are characterized by the property that every two nonzero submodules have nonzero intersection, ensuring a strong form of indecomposability. Pure submodules, defined by preserving the exactness of sequences under tensor products, maintain structural integrity relative to the ambient module, especially in relation to flat modules. Uniform submodules emphasize internal cohesion through intersection properties, while pure submodules focus on preserving algebraic relations through purity conditions in module extensions.
Uniform submodule Infographic
 libterm.com
libterm.com