A compact set in mathematics is a set that is both closed and bounded, ensuring every open cover has a finite subcover. This property is fundamental in analysis and topology, providing critical insights into continuity, convergence, and function behavior. Explore the rest of the article to deepen your understanding of how compactness influences various mathematical concepts.
Table of Comparison
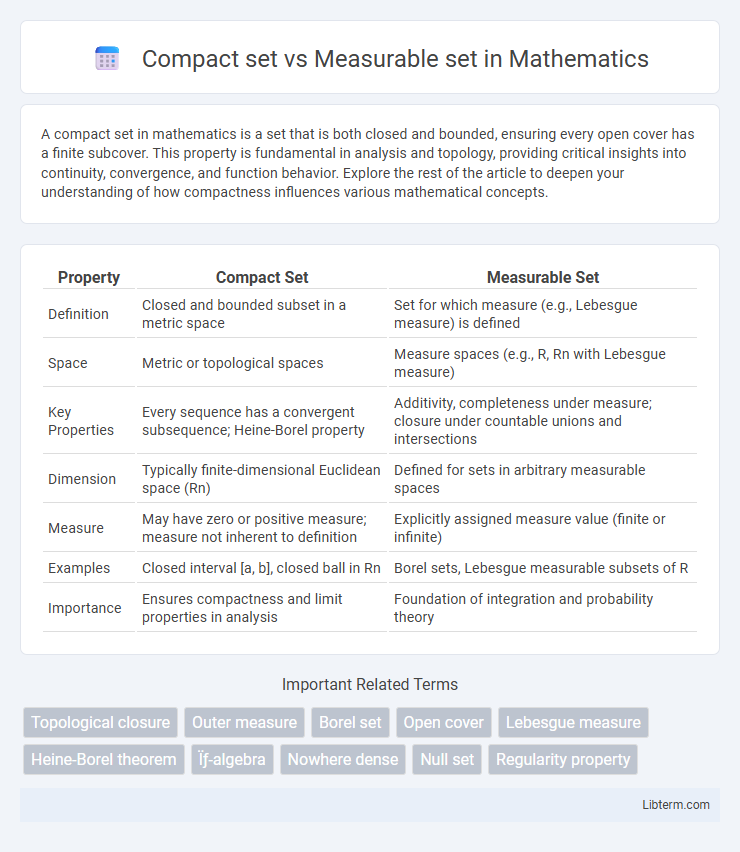
| Property | Compact Set | Measurable Set |
|---|---|---|
| Definition | Closed and bounded subset in a metric space | Set for which measure (e.g., Lebesgue measure) is defined |
| Space | Metric or topological spaces | Measure spaces (e.g., R, Rn with Lebesgue measure) |
| Key Properties | Every sequence has a convergent subsequence; Heine-Borel property | Additivity, completeness under measure; closure under countable unions and intersections |
| Dimension | Typically finite-dimensional Euclidean space (Rn) | Defined for sets in arbitrary measurable spaces |
| Measure | May have zero or positive measure; measure not inherent to definition | Explicitly assigned measure value (finite or infinite) |
| Examples | Closed interval [a, b], closed ball in Rn | Borel sets, Lebesgue measurable subsets of R |
| Importance | Ensures compactness and limit properties in analysis | Foundation of integration and probability theory |
Introduction to Compact and Measurable Sets
Compact sets in topology are defined by their property that every open cover has a finite subcover, ensuring limit points are contained within the set, which is crucial for analysis and topology. Measurable sets, fundamental in measure theory, are subsets of a given space for which a measure, like Lebesgue measure, can be consistently defined, allowing for the formal integration and probability assignment. Understanding the distinction between compactness in topological spaces and measurability in measure spaces underpins many advanced concepts in mathematical analysis and probability theory.
Defining Compact Sets: Key Properties
Compact sets in topology are defined as subsets of a space where every open cover has a finite subcover, ensuring completeness and total boundedness in metric spaces. These sets are closed and bounded in Euclidean spaces, which distinguishes them from merely measurable sets that satisfy criteria based on measure theory rather than topological properties. Key properties of compact sets include sequential compactness, limit point compactness, and preservation under continuous mappings, highlighting their foundational role in analysis and topology.
Understanding Measurable Sets in Measure Theory
In measure theory, measurable sets are those for which a measure, such as the Lebesgue measure, can be consistently defined, allowing the assignment of a size or volume to potentially complex or irregular subsets of a space. Compact sets, in contrast, are topologically closed and bounded, often simplifying measure considerations but not guaranteeing measurability in all contexts. Understanding measurable sets involves grasping sigma-algebras and Caratheodory's criterion, essential tools for extending measures beyond simple intervals to more abstract sets in real analysis.
Topological Foundations: Open and Closed Sets
Compact sets in topology are defined by every open cover having a finite subcover, emphasizing their relationship with open sets. Measurable sets, particularly in measure theory, are characterized by their compatibility with a given sigma-algebra, often generated by open or closed sets, ensuring that their measure is well-defined. The concept of compactness highlights topological closure properties, while measurability underscores set-theoretic structures allowing integration and measure assignment.
Criteria for Compactness in Metric Spaces
In metric spaces, a set is compact if and only if it is closed and totally bounded, meaning every sequence has a convergent subsequence whose limit lies within the set. Measurable sets, defined via Lebesgue measure, focus on the ability to assign a consistent measure rather than topological properties like closure or boundedness. Unlike measurable sets, compact sets guarantee limit point inclusion and finite subcover existence, essential criteria for compactness evaluation.
Measurability: Sigma-Algebras and Measures
Measurable sets are defined within the framework of sigma-algebras, which are collections of subsets closed under countable unions, intersections, and complements, ensuring a consistent notion of measure. Compact sets, crucial in topology, do not inherently guarantee measurability unless they belong to a sigma-algebra associated with a given measure space, such as the Borel sigma-algebra on a topological space. The interplay between compactness and measurability is essential in measure theory, as every compact set in a metrizable space is Borel measurable, allowing the application of measures like the Lebesgue measure.
Relationship Between Compactness and Measurability
Compact sets in Euclidean space are always measurable with respect to the Lebesgue measure, as they are closed and bounded, ensuring finite measure. Measurable sets, however, need not be compact; they can be unbounded or lack closure, but still have well-defined Lebesgue measures. The relationship highlights that compactness implies measurability, but measurability does not imply compactness, crucial in analysis for integrating functions over well-behaved domains.
Examples: Compact Sets vs. Measurable Sets
Compact sets such as the closed interval [0,1] in R illustrate sets that are bounded and closed, ensuring every open cover has a finite subcover, while measurable sets include more general examples like the Cantor set, which is uncountably infinite and has Lebesgue measure zero. An example showing the distinction involves non-measurable sets constructed via the Vitali construction, which are not compact and lack a well-defined Lebesgue measure. In contrast, compact sets in Euclidean spaces are always measurable with finite measure, clarifying the inclusion of compact sets within the class of measurable sets but not vice versa.
Applications in Analysis and Probability
Compact sets provide crucial properties such as closedness and boundedness that simplify optimization problems and ensure the existence of maximum or minimum values in analysis. Measurable sets form the foundation of measure theory, enabling the rigorous definition of integrals and probabilities in probability theory. The interplay between compactness and measurability facilitates advanced techniques in stochastic processes, functional analysis, and ergodic theory, enhancing the study of convergence and distribution of random variables.
Summary: Comparing Compact and Measurable Sets
Compact sets in topology are closed and bounded subsets of Euclidean space, ensuring every open cover has a finite subcover, which guarantees properties like limit point compactness and completeness. Measurable sets, fundamental in measure theory, are subsets for which a measure (such as the Lebesgue measure) is well-defined, allowing integration and probability assignments. While compactness relates to topological structure and convergence, measurability focuses on assigning consistent sizes or volumes, and they intersect in contexts like compact subsets of measurable spaces being measurable with finite measure.
Compact set Infographic
 libterm.com
libterm.com