The mapping class group captures symmetries of surfaces by classifying homeomorphisms up to isotopy, playing a crucial role in topology and geometric group theory. Understanding its structure helps reveal deep connections between algebraic, geometric, and dynamical properties of surfaces. Explore the rest of this article to discover how the mapping class group influences modern mathematical research and applications.
Table of Comparison
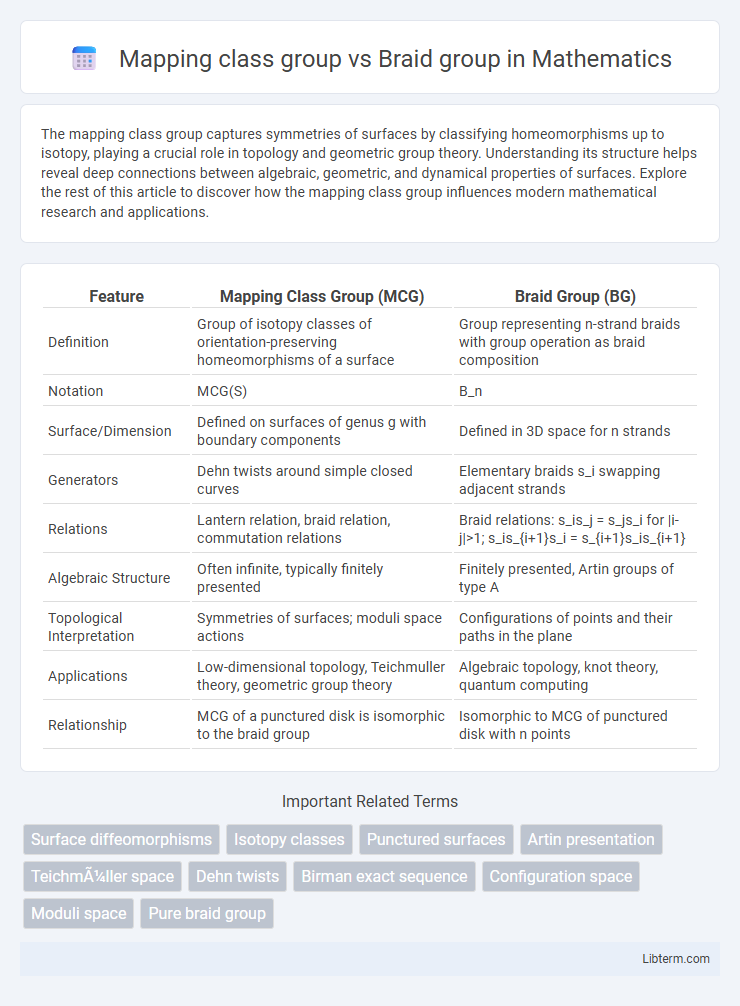
| Feature | Mapping Class Group (MCG) | Braid Group (BG) |
|---|---|---|
| Definition | Group of isotopy classes of orientation-preserving homeomorphisms of a surface | Group representing n-strand braids with group operation as braid composition |
| Notation | MCG(S) | B_n |
| Surface/Dimension | Defined on surfaces of genus g with boundary components | Defined in 3D space for n strands |
| Generators | Dehn twists around simple closed curves | Elementary braids s_i swapping adjacent strands |
| Relations | Lantern relation, braid relation, commutation relations | Braid relations: s_is_j = s_js_i for |i-j|>1; s_is_{i+1}s_i = s_{i+1}s_is_{i+1} |
| Algebraic Structure | Often infinite, typically finitely presented | Finitely presented, Artin groups of type A |
| Topological Interpretation | Symmetries of surfaces; moduli space actions | Configurations of points and their paths in the plane |
| Applications | Low-dimensional topology, Teichmuller theory, geometric group theory | Algebraic topology, knot theory, quantum computing |
| Relationship | MCG of a punctured disk is isomorphic to the braid group | Isomorphic to MCG of punctured disk with n points |
Introduction to Mapping Class Groups and Braid Groups
Mapping class groups describe isotopy classes of orientation-preserving homeomorphisms of surfaces and play a crucial role in the study of 2-dimensional topology and geometric group theory. Braid groups, defined by Artin, encode the algebraic structure of braids as isotopy classes of strand arrangements in 3-dimensional space and serve as fundamental examples of mapping class groups for the punctured disk. Understanding the relationship between mapping class groups and braid groups reveals deep connections between surface diffeomorphisms and algebraic structures arising from configurations of points in the plane.
Historical Background and Development
The Mapping Class Group, first rigorously studied by Max Dehn in the early 20th century, arose from investigations into surface topology and the classification of surface homeomorphisms. The Braid Group, introduced by Emil Artin in 1925, originally captured the algebraic structure underlying braids and their isotopy classes in three-dimensional space. Both groups fundamentally contribute to geometric group theory, with the Mapping Class Group focusing on isotopy classes of diffeomorphisms of surfaces, while the Braid Group models configurations of points in the plane, revealing deep connections through monodromy and configuration spaces.
Defining the Mapping Class Group
The Mapping Class Group of a surface is defined as the group of isotopy classes of orientation-preserving homeomorphisms of that surface. It captures the symmetries of the surface by considering continuous deformations rather than just rigid transformations. This group generalizes the Braid Group, which can be seen as the Mapping Class Group of a punctured disk, linking topological surface transformations with braid theory.
Understanding the Braid Group
The braid group, denoted \( B_n \), consists of \( n \)-strand braids with group operation defined by concatenation, capturing the fundamental group of the configuration space of \( n \) distinct points in the plane. Understanding the braid group involves analyzing its generators, the elementary braids \( \sigma_i \), and the defining Artin relations, which govern how strands intertwine without crossing over themselves. The mapping class group of a punctured disk is isomorphic to the braid group, providing a geometric interpretation for braid group elements as isotopy classes of homeomorphisms fixing the boundary.
Algebraic Structures and Generators
The Mapping Class Group is an algebraic structure representing isotopy classes of orientation-preserving diffeomorphisms of a surface, typically generated by Dehn twists around simple closed curves. The Braid Group, defined algebraically by Artin's presentation, is generated by elementary braid generators subject to specific braid relations reflecting the over- and under-crossings of strands. While both groups exhibit rich combinatorial properties, the Mapping Class Group generalizes braid relations by incorporating surface topology, making its generators correspond to more complex surface homeomorphisms compared to the linear strand interchanges in Braid Groups.
Geometric Interpretations
The mapping class group of a surface represents isotopy classes of orientation-preserving homeomorphisms, capturing geometric transformations of the surface, while the braid group encodes configurations of points moving in the plane without collisions. Geometrically, the braid group acts as the fundamental group of the configuration space of distinct points, highlighting paths of particle exchanges, whereas the mapping class group organizes surface symmetries up to continuous deformation. These interpretations link the braid group to punctured disks and the mapping class group to more general surfaces, revealing their roles in topology and geometric group theory.
Key Similarities and Differences
The Mapping Class Group of a surface and the Braid Group both describe fundamental symmetries and transformations tied to topological spaces, with the Mapping Class Group encoding isotopy classes of orientation-preserving diffeomorphisms and the Braid Group representing braids as isotopy classes of strand movements in a disk. Both groups can be presented by generators and relations, with the Braid Group often viewed as a subgroup or quotient of the Mapping Class Group of a punctured disk. Key differences include the Mapping Class Group's broader applicability to various surfaces and its connections to Teichmuller theory, while the Braid Group specializes in configurations of points and underpins knot theory and algebraic structures such as Artin groups.
Applications in Topology and Algebra
The mapping class group, representing isotopy classes of homeomorphisms of a surface, plays a crucial role in the study of Teichmuller spaces and moduli spaces of Riemann surfaces, offering insights into 3-manifold topology and geometric group theory. The braid group, generated by strands interchanging positions, finds applications in knot theory and algebraic structures such as Artin groups, impacting fields like quantum computing and statistical mechanics. Both groups provide foundational frameworks for understanding fiber bundles, monodromy representations, and the interplay between algebraic and geometric properties in low-dimensional topology.
Relationships with Other Mathematical Groups
The mapping class group of a surface generalizes the braid group by considering isotopy classes of homeomorphisms, connecting directly to the fundamental group and automorphism groups of free groups. Braid groups embed into mapping class groups as those preserving punctures, linking algebraic and geometric group theory through surface topology. Both groups relate to Artin groups and Coxeter groups, highlighting their roles in categorifying symmetries and studying configuration spaces in mathematics.
Recent Research and Open Problems
Recent research on the mapping class group and braid group explores their deep algebraic structures, focusing on their actions on surfaces and configuration spaces, respectively, to understand low-dimensional topology and geometric group theory. Open problems include characterizing injective homomorphisms between these groups and determining the full structure of their automorphism groups, which impacts the study of Teichmuller spaces and 3-manifolds. Advances in categorical and quantum approaches offer promising tools for resolving questions about their relationships and representations.
Mapping class group Infographic
 libterm.com
libterm.com