A congruence class groups numbers sharing the same remainder when divided by a specific modulus, forming an essential concept in modular arithmetic and number theory. Understanding how these classes interact helps simplify complex calculations and solve equations across various fields like cryptography and computer science. Explore the article to deepen your grasp of congruence classes and their practical applications.
Table of Comparison
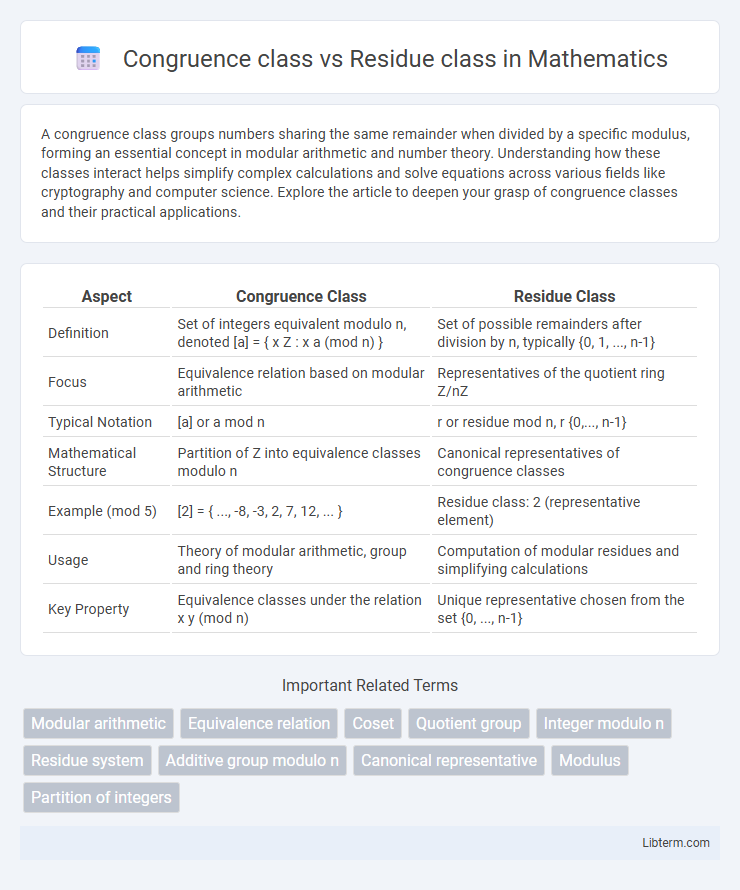
| Aspect | Congruence Class | Residue Class |
|---|---|---|
| Definition | Set of integers equivalent modulo n, denoted [a] = { x Z : x a (mod n) } | Set of possible remainders after division by n, typically {0, 1, ..., n-1} |
| Focus | Equivalence relation based on modular arithmetic | Representatives of the quotient ring Z/nZ |
| Typical Notation | [a] or a mod n | r or residue mod n, r {0,..., n-1} |
| Mathematical Structure | Partition of Z into equivalence classes modulo n | Canonical representatives of congruence classes |
| Example (mod 5) | [2] = { ..., -8, -3, 2, 7, 12, ... } | Residue class: 2 (representative element) |
| Usage | Theory of modular arithmetic, group and ring theory | Computation of modular residues and simplifying calculations |
| Key Property | Equivalence classes under the relation x y (mod n) | Unique representative chosen from the set {0, ..., n-1} |
Introduction to Modular Arithmetic
In modular arithmetic, a congruence class represents all integers that share the same remainder when divided by a fixed modulus, effectively grouping numbers based on their equivalence under modular congruence. A residue class, often used interchangeably with congruence class, specifically refers to the set of all integers congruent to a particular residue modulo n. Understanding these classes is fundamental in number theory for solving problems involving divisibility, cryptography, and algebraic structures.
Defining Congruence Class
A congruence class modulo \( n \) is the set of all integers that share the same remainder when divided by \( n \), formally defined as \([a]_n = \{ x \in \mathbb{Z} \mid x \equiv a \pmod{n} \}\). This equivalence relation partitions the integers into distinct congruence classes, where two integers are congruent if their difference is divisible by \( n \). Residue classes represent these congruence classes as canonical representatives, typically chosen from the set \(\{0, 1, \ldots, n-1\}\).
Understanding Residue Class
A residue class refers to the set of all integers that leave the same remainder when divided by a fixed modulus n, symbolized as [a]_n, where a is a representative integer. Understanding residue classes is crucial in modular arithmetic, as they partition the integers into n distinct classes, each corresponding to one possible remainder from 0 to n-1. Residue classes simplify calculations in number theory by allowing equivalence relations based on congruences, making them fundamental in solving congruence equations and in group theory applications.
Key Differences Between Congruence and Residue Classes
Congruence classes are sets of integers that share the same remainder when divided by a modulus, forming equivalence classes under modular arithmetic. Residue classes specifically refer to the distinct possible remainders modulo a number, representing canonical representatives of these congruence classes. The key difference lies in that a congruence class groups all integers equivalent under modulo operation, while a residue class identifies particular representative elements within those classes.
Mathematical Representation and Notation
A congruence class modulo \( n \) is represented by the set \([a]_n = \{ x \in \mathbb{Z} \mid x \equiv a \pmod{n} \}\), where all integers \( x \) satisfy the congruence relation \( x \equiv a \ (\text{mod } n) \). The residue class is synonymous with the congruence class but often emphasizes elements in the ring of integers modulo \( n \), denoted as \(\mathbb{Z}/n\mathbb{Z}\), where each residue class corresponds to a distinct equivalence class under the modulo operation. Notation-wise, both terms utilize brackets or parentheses and the modulo symbol to denote the equivalence relation, such as \([a]_n\) or \(a \bmod n\), reflecting their shared mathematical structure.
Properties of Congruence Classes
Congruence classes are sets of integers that share the same remainder when divided by a fixed modulus, exhibiting properties like closure under addition, subtraction, and multiplication modulo the modulus. Each congruence class forms an equivalence class in modular arithmetic, ensuring reflexivity, symmetry, and transitivity. These properties enable the creation of well-defined arithmetic in the ring of integers modulo n, commonly denoted as Z/nZ.
Properties of Residue Classes
Residue classes, defined modulo a positive integer \( n \), partition the set of integers into disjoint subsets where each class contains integers congruent modulo \( n \). Key properties include closure under addition, subtraction, and multiplication, ensuring that arithmetic operations on representatives yield results within the same residue class. Each residue class corresponds uniquely to an element in the ring \( \mathbb{Z}/n\mathbb{Z} \), forming a finite cyclic group with cardinality \( n \).
Practical Examples in Number Theory
In number theory, a congruence class modulo n consists of all integers that yield the same remainder when divided by n, exemplified by the set of numbers congruent to 3 mod 5: {..., -7, -2, 3, 8, 13, ...}. Residue classes are specific representatives chosen from each congruence class, often the smallest non-negative integers {0, 1, 2, ..., n-1}. Practical applications include solving linear congruences, cryptographic algorithms like RSA, and modular arithmetic operations in computer science.
Applications in Cryptography and Coding Theory
Congruence classes and residue classes are fundamental in modular arithmetic, forming the basis of many cryptographic algorithms and error-correcting codes. In cryptography, residue classes enable secure key generation and encryption schemes such as RSA and Diffie-Hellman by operating within finite fields and rings defined by modular congruences. Coding theory leverages congruence classes to construct linear codes and cyclic codes, which are essential for detecting and correcting errors in data transmission.
Summary: Choosing the Right Terminology
Selecting between congruence class and residue class depends on the mathematical context and audience familiarity; congruence class is often used in modular arithmetic emphasizing equivalence relations, while residue class highlights the representative elements within modular systems. Congruence classes group integers based on a specified modulus, illustrating partitions of the integer set, whereas residue classes focus on the remainder values as canonical representatives. Precise terminology enhances clarity in algebraic structures and number theory applications, ensuring effective communication of modular concepts.
Congruence class Infographic
 libterm.com
libterm.com