Singular cohomology is a fundamental tool in algebraic topology used to classify and measure the features of topological spaces by assigning algebraic invariants. It involves defining cochains on singular simplices, which are continuous maps from standard simplices into the space, and then computing their cohomology groups to reveal topological properties such as holes and structure. Explore the rest of this article to understand how singular cohomology applies to diverse mathematical contexts and enhances your grasp of topology.
Table of Comparison
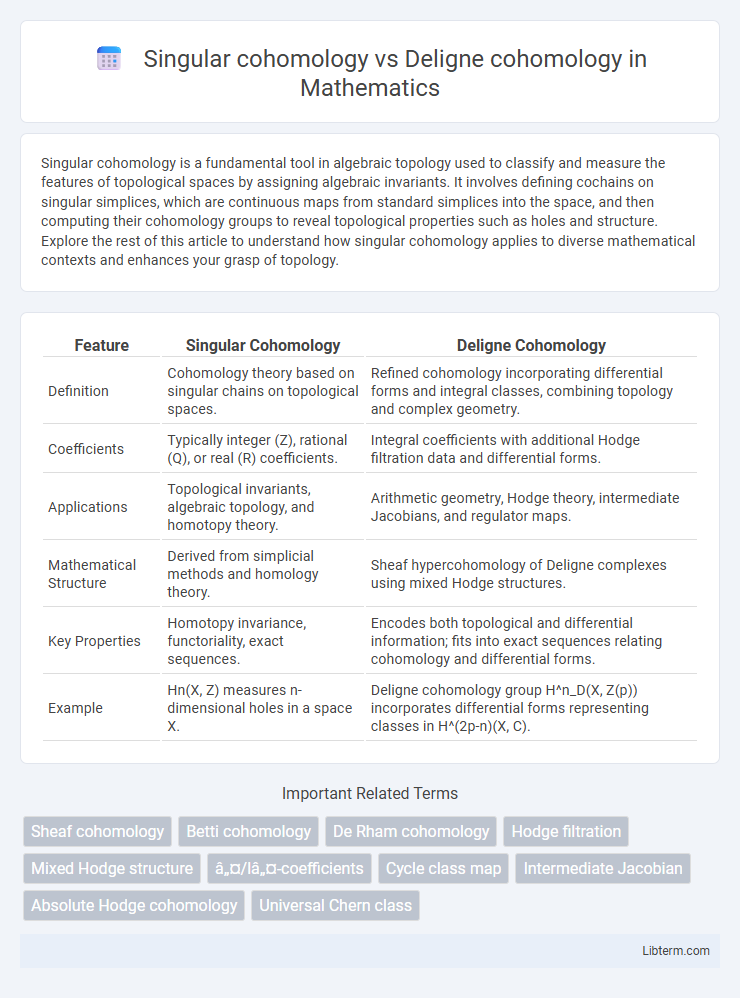
| Feature | Singular Cohomology | Deligne Cohomology |
|---|---|---|
| Definition | Cohomology theory based on singular chains on topological spaces. | Refined cohomology incorporating differential forms and integral classes, combining topology and complex geometry. |
| Coefficients | Typically integer (Z), rational (Q), or real (R) coefficients. | Integral coefficients with additional Hodge filtration data and differential forms. |
| Applications | Topological invariants, algebraic topology, and homotopy theory. | Arithmetic geometry, Hodge theory, intermediate Jacobians, and regulator maps. |
| Mathematical Structure | Derived from simplicial methods and homology theory. | Sheaf hypercohomology of Deligne complexes using mixed Hodge structures. |
| Key Properties | Homotopy invariance, functoriality, exact sequences. | Encodes both topological and differential information; fits into exact sequences relating cohomology and differential forms. |
| Example | Hn(X, Z) measures n-dimensional holes in a space X. | Deligne cohomology group H^n_D(X, Z(p)) incorporates differential forms representing classes in H^(2p-n)(X, C). |
Introduction to Singular and Deligne Cohomology
Singular cohomology provides a fundamental topological invariant capturing global properties of topological spaces using simplicial complexes and continuous mappings. Deligne cohomology refines this by integrating differential forms and algebraic cycles, linking topological data with Hodge theory and arithmetic geometry. Key distinctions lie in singular cohomology's purely topological nature versus Deligne cohomology's mixed analytic and algebraic structure facilitating the study of intermediate Jacobians and regulators.
Historical Background and Motivation
Singular cohomology, developed in the early 20th century by mathematicians such as Eilenberg and Steenrod, provides a fundamental tool for classifying topological spaces via homotopy-invariant cohomological invariants. Deligne cohomology, introduced by Pierre Deligne in the 1970s, emerged to refine classical cohomological theories by integrating both differential and integral structures, particularly to capture finer geometric and arithmetic information on complex algebraic varieties. The motivation behind Deligne cohomology lies in addressing limitations of singular cohomology by incorporating Hodge theory and algebraic cycles, enabling applications in motivic cohomology and the study of regulators in arithmetic geometry.
Foundations: Definitions and Constructions
Singular cohomology is defined using the cochain complex of singular simplices on a topological space, providing a purely topological invariant capturing information about the space's global structure through homology classes. Deligne cohomology extends singular cohomology by incorporating differential forms and sheaf theory, combining topological and geometric data via hypercohomology of the Deligne complex, which includes smooth forms and integral coefficients. The construction of Deligne cohomology relies on the interplay between sheaf complexes, Cech resolutions, and differential forms, making it a refined tool for studying characteristic classes and mixed Hodge structures beyond the topological invariants given by singular cohomology.
Topological vs. Algebraic Geometry Perspectives
Singular cohomology, central to algebraic topology, uses continuous maps of simplices into topological spaces to capture global topological invariants, making it essential for analyzing general topological spaces. Deligne cohomology integrates differential forms with integral cohomology classes, bridging algebraic and analytical perspectives, and is particularly relevant in algebraic geometry for describing variations of Hodge structures and mixed motives. The topological viewpoint emphasizes homotopy invariance and simplicial methods, while the algebraic geometric approach leverages sheaf theory and the language of derived categories to encode refined arithmetic and geometric information.
Singular Cohomology: Key Properties and Applications
Singular cohomology, a fundamental tool in algebraic topology, assigns cohomology groups to topological spaces using singular simplices, capturing essential topological invariants such as Betti numbers. Its functoriality, homotopy invariance, and exactness in Mayer-Vietoris sequences enable effective computations and classification of spaces. Applications include detecting holes in manifolds, classifying fiber bundles, and supporting Poincare duality crucial in geometric analysis.
Deligne Cohomology: Structure and Significance
Deligne cohomology integrates sheaf cohomology and differential forms to capture finer geometric and topological information than singular cohomology alone. Its structure combines the algebraic and analytic aspects of complex manifolds, encoding data about line bundles with connections and characteristic classes. The significance of Deligne cohomology lies in its ability to refine classical invariants, playing a crucial role in arithmetic geometry, Hodge theory, and the study of regulator maps.
Comparing Cohomological Invariants
Singular cohomology provides topological invariants derived from continuous maps of simplices, effectively capturing global topological properties through cohomology classes with coefficients in abelian groups. Deligne cohomology refines these invariants by integrating differential forms and integral data, offering a hybrid approach that combines de Rham cohomology with integral cohomology to encode both topological and geometric information. Compared to singular cohomology, Deligne cohomology enables the classification of more nuanced geometric structures such as line bundles with connection, making it crucial in arithmetic geometry and the study of algebraic cycles with additional differential data.
Interrelations: Maps and Exact Sequences
Singular cohomology and Deligne cohomology are interconnected through natural transformation maps that respect their respective cochain complexes, allowing the translation of topological data into sheaf-theoretic contexts. Exact sequences such as the exponential sequence in Deligne cohomology induce long exact sequences relating singular cohomology with integral coefficients to Deligne cohomology groups, facilitating computations in arithmetic and differential geometry. These interrelations enable the interpretation of Deligne cohomology classes as differential characters, bridging the gap between smooth differential forms and integral singular cohomology classes.
Applications in Algebraic Cycles and Hodge Theory
Singular cohomology provides a topological invariant capturing global properties of algebraic varieties, essential for studying algebraic cycles through cycle class maps. Deligne cohomology refines this by incorporating differential forms with integral coefficients, bridging Hodge theory and algebraic cycles to detect finer arithmetic and geometric structures, such as intermediate Jacobians. In Hodge theory, Deligne cohomology plays a critical role in the formulation of the Hodge conjecture and the description of regulators in arithmetic geometry, offering a richer framework for understanding the interaction between complex geometry and algebraic cycles.
Current Research Directions and Open Problems
Current research in singular cohomology versus Deligne cohomology explores the integration of differential-geometric and topological data to refine characteristic classes and invariants in algebraic and differential geometry. Open problems include extending Deligne cohomology theories to broader categories such as derived algebraic geometry or non-commutative spaces, and resolving the challenges in computational methods for explicit cycle representatives corresponding to transcendental classes. Further investigation targets the comparison of regulator maps and their role in linking arithmetic and motivic cohomology through refined cohomological frameworks.
Singular cohomology Infographic
 libterm.com
libterm.com