Maass forms are complex-valued eigenfunctions of the hyperbolic Laplacian that remain invariant under the action of a discrete subgroup of SL(2, R), playing a crucial role in modern number theory and the theory of automorphic forms. These non-holomorphic analogs of modular forms are essential in understanding spectral theory, L-functions, and quantum chaos. Explore the rest of the article to deepen your understanding of Maass forms and their significant applications.
Table of Comparison
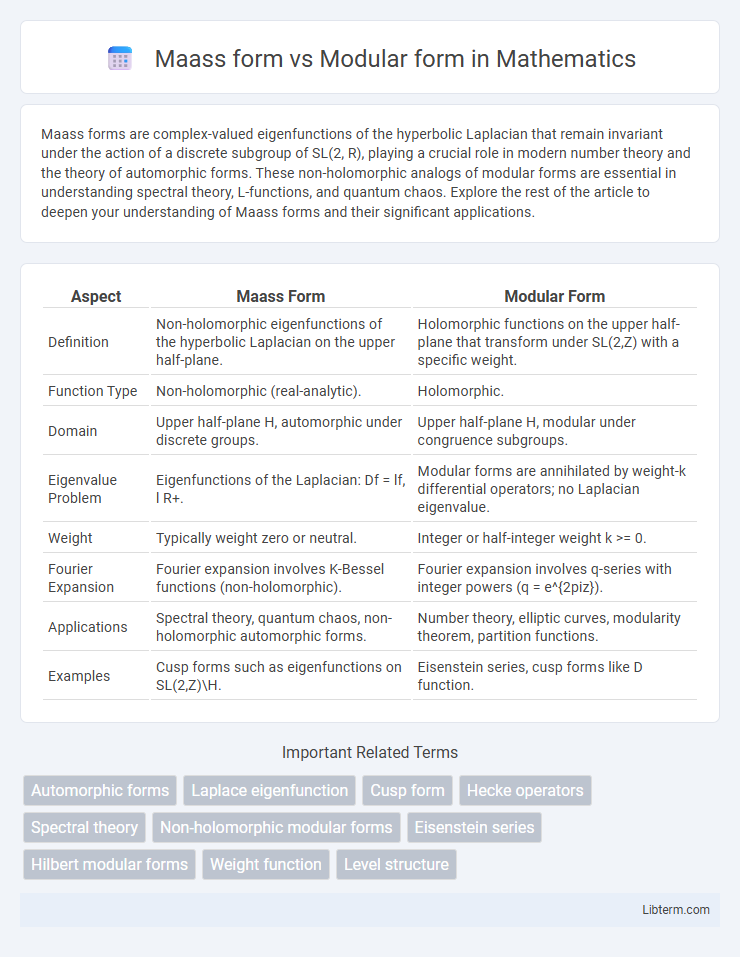
| Aspect | Maass Form | Modular Form |
|---|---|---|
| Definition | Non-holomorphic eigenfunctions of the hyperbolic Laplacian on the upper half-plane. | Holomorphic functions on the upper half-plane that transform under SL(2,Z) with a specific weight. |
| Function Type | Non-holomorphic (real-analytic). | Holomorphic. |
| Domain | Upper half-plane H, automorphic under discrete groups. | Upper half-plane H, modular under congruence subgroups. |
| Eigenvalue Problem | Eigenfunctions of the Laplacian: Df = lf, l R+. | Modular forms are annihilated by weight-k differential operators; no Laplacian eigenvalue. |
| Weight | Typically weight zero or neutral. | Integer or half-integer weight k >= 0. |
| Fourier Expansion | Fourier expansion involves K-Bessel functions (non-holomorphic). | Fourier expansion involves q-series with integer powers (q = e^{2piz}). |
| Applications | Spectral theory, quantum chaos, non-holomorphic automorphic forms. | Number theory, elliptic curves, modularity theorem, partition functions. |
| Examples | Cusp forms such as eigenfunctions on SL(2,Z)\H. | Eisenstein series, cusp forms like D function. |
Introduction to Automorphic Forms
Maass forms are non-holomorphic eigenfunctions of the hyperbolic Laplacian on the upper half-plane, exhibiting automorphic properties under discrete groups like SL(2,Z). Modular forms, in contrast, are holomorphic functions satisfying specific transformation laws under the modular group with growth conditions at cusps. Both Maass and modular forms serve as fundamental objects in the theory of automorphic forms, connecting number theory, representation theory, and the spectral theory of automorphic Laplacians.
Defining Modular Forms
Modular forms are complex analytic functions defined on the upper half-plane that satisfy specific transformation properties under the action of the modular group SL(2, Z) and exhibit growth conditions at cusps. These functions are holomorphic, possess a Fourier expansion, and play a critical role in number theory, particularly in the theory of elliptic curves and L-functions. Unlike Maass forms, which are non-holomorphic eigenfunctions of the Laplacian operator, modular forms emphasize holomorphicity and algebraic structures in their definition.
Understanding Maass Forms
Maass forms are non-holomorphic automorphic forms that generalize classical modular forms by relaxing the holomorphicity condition while preserving eigenfunction properties under the hyperbolic Laplacian. These forms exhibit rich spectral behavior and are essential in the study of quantum chaos, number theory, and the spectral theory of automorphic operators. Understanding Maass forms involves analyzing their eigenvalues, Fourier coefficients, and symmetry properties within the framework of the modular group action on the upper half-plane.
Historical Context and Origins
Maass forms originated in the mid-20th century through the work of Hans Maass, expanding the classical theory of modular forms by introducing non-holomorphic eigenfunctions of the Laplace operator on the upper half-plane. Modular forms trace back to the 19th century, rooted in the study of elliptic functions and complex analysis, with significant contributions from mathematicians such as Bernhard Riemann and Felix Klein. The development of Maass forms provided a crucial link between harmonic analysis and number theory, enriching the spectral theory of automorphic forms beyond the holomorphic framework established by classical modular forms.
Key Mathematical Differences
Maass forms are non-holomorphic eigenfunctions of the hyperbolic Laplacian on the upper half-plane, whereas modular forms are holomorphic functions satisfying specific transformation properties under the action of the modular group. Unlike modular forms, which are characterized by their weight and Fourier expansions with algebraic coefficients, Maass forms are typically real-analytic and possess eigenvalues associated with the Laplace operator. These key mathematical differences highlight the distinct roles of Maass forms in spectral theory and modular forms in complex analysis and arithmetic geometry.
Transformation Properties
Maass forms transform under the action of the modular group with eigenvalues corresponding to non-holomorphic Laplacian operators, exhibiting automorphy but lacking holomorphicity. Modular forms, in contrast, are holomorphic functions on the upper half-plane that satisfy specific transformation rules under the modular group with integral or half-integral weights. Both structures encode rich arithmetic information, yet Maass forms generalize modular forms by relaxing holomorphic constraints while preserving modular symmetry through their transformation properties.
Analytic versus Holomorphic Nature
Maass forms are non-holomorphic automorphic forms characterized by eigenfunctions of the hyperbolic Laplacian with real eigenvalues, whereas modular forms are holomorphic functions on the upper half-plane satisfying specific transformation properties under the modular group. The analytic nature of Maass forms involves smoothness and eigenvalue equations without holomorphy, contrasting with modular forms whose structure depends crucially on complex differentiability. This distinction highlights the fundamental difference in analytic behavior, with Maass forms extending the theory of automorphic forms beyond holomorphic contexts.
Spectral Theory and Eigenvalues
Maass forms are non-holomorphic automorphic forms characterized by eigenvalues of the hyperbolic Laplacian, distinguishing them from classical holomorphic modular forms, which emerge from analytic functions on the upper half-plane. In spectral theory, Maass forms contribute to the discrete spectrum of the Laplacian on modular curves, with eigenvalues corresponding to their spectral parameters; modular forms primarily relate to the cuspidal spectrum via Hecke operators. The study of eigenvalues in Maass forms advances the understanding of quantum chaos and arithmetic quantum unique ergodicity, while modular form eigenvalues connect deeply with arithmetic geometry through eigenforms and L-functions.
Applications in Number Theory and Physics
Maass forms, non-holomorphic eigenfunctions of the hyperbolic Laplacian, play a crucial role in analytic number theory, particularly in the spectral theory of automorphic forms and the study of L-functions, revealing deep connections between prime numbers and quantum chaos. Modular forms, holomorphic functions on the upper half-plane with transformation properties under the action of the modular group, are essential in solving problems in arithmetic geometry, partition theory, and the proof of Fermat's Last Theorem through their relation to elliptic curves. In physics, Maass forms appear in quantum chaos and string theory, while modular forms underpin dualities in conformal field theory and the counting of black hole microstates.
Comparing Maass and Modular Forms: Summary
Maass forms are non-holomorphic automorphic forms characterized by eigenvalues of the Laplace operator, contrasting with modular forms, which are holomorphic functions with complex analytic properties on the upper half-plane. Both forms hold crucial roles in number theory and representation theory, with Maass forms associated with real-analytic eigenfunctions and modular forms linked to complex analytic functions displaying modularity under SL(2, Z) action. The spectral theory of Maass forms complements the algebraic and arithmetic properties of modular forms, highlighting their distinct yet interconnected significance in modern mathematics.
Maass form Infographic
 libterm.com
libterm.com