A linear equation represents a relationship between two variables where the graph forms a straight line, typically written in the form y = mx + b, with m as the slope and b as the y-intercept. Understanding how to solve and manipulate these equations is crucial for applications in algebra, economics, and engineering. Explore the rest of this article to master solving linear equations and applying them to real-world problems.
Table of Comparison
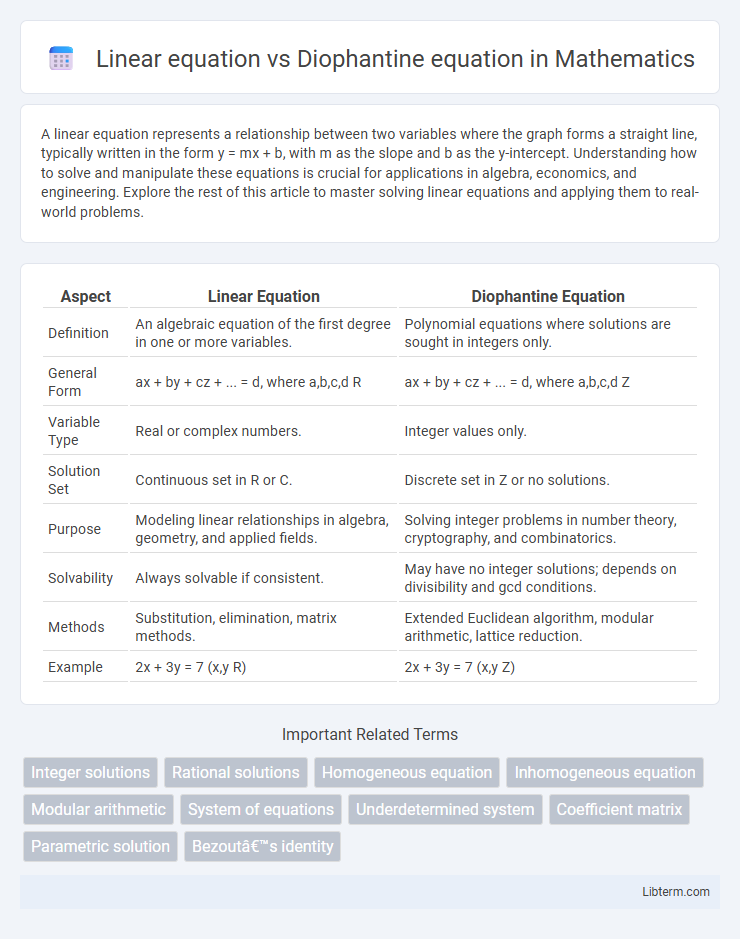
| Aspect | Linear Equation | Diophantine Equation |
|---|---|---|
| Definition | An algebraic equation of the first degree in one or more variables. | Polynomial equations where solutions are sought in integers only. |
| General Form | ax + by + cz + ... = d, where a,b,c,d R | ax + by + cz + ... = d, where a,b,c,d Z |
| Variable Type | Real or complex numbers. | Integer values only. |
| Solution Set | Continuous set in R or C. | Discrete set in Z or no solutions. |
| Purpose | Modeling linear relationships in algebra, geometry, and applied fields. | Solving integer problems in number theory, cryptography, and combinatorics. |
| Solvability | Always solvable if consistent. | May have no integer solutions; depends on divisibility and gcd conditions. |
| Methods | Substitution, elimination, matrix methods. | Extended Euclidean algorithm, modular arithmetic, lattice reduction. |
| Example | 2x + 3y = 7 (x,y R) | 2x + 3y = 7 (x,y Z) |
Introduction to Linear and Diophantine Equations
Linear equations involve expressions of the form ax + b = 0, where a and b are real numbers, focusing on finding solutions within the real or complex number systems. Diophantine equations, named after the ancient mathematician Diophantus, specifically seek integer solutions to polynomial equations, commonly in the form ax + by = c for integers a, b, and c. The key distinction lies in the solution domain: linear equations allow any number from a continuous set, whereas Diophantine equations restrict solutions to discrete integers, making their solvability more complex and significant in number theory.
Definitions: Linear Equations Explained
Linear equations are algebraic expressions representing a straight line, typically written in the form ax + b = 0, where a and b are constants and x is the variable. Diophantine equations, a subset of linear equations, specifically require integer solutions to equations like ax + by = c, with a, b, c as integers. Unlike general linear equations that may have real or complex solutions, Diophantine equations emphasize whole-number solutions important in number theory and integer programming.
Understanding Diophantine Equations
Diophantine equations are polynomial equations where integer solutions are sought, distinguishing them from general linear equations that allow real or complex solutions. These equations often involve multiple variables and require finding sets of integers that satisfy the equation simultaneously, making them a core topic in number theory. The study of Diophantine equations focuses on solvability, characterization of solutions, and the development of algorithms, such as the Euclidean algorithm for linear Diophantine equations.
Fundamental Differences Between Linear and Diophantine Equations
Linear equations involve variables with coefficients and constants typically in real or complex numbers, aiming to find all solutions that satisfy the equation. Diophantine equations specifically require integer solutions, often leading to more complex problem-solving techniques and constraints. The fundamental difference lies in the solution domain: linear equations allow continuous solutions, while Diophantine equations restrict solutions to discrete integers.
Solution Methods for Linear Equations
Solution methods for linear equations primarily involve algebraic techniques such as substitution, elimination, and matrix operations including Gaussian elimination. These methods aim to find exact values for variables that satisfy the linear equation or system of equations. In contrast to Diophantine equations, which require integer solutions and often use number theory approaches, linear equations allow for a broader set of solutions including real or complex numbers.
Techniques for Solving Diophantine Equations
Techniques for solving Diophantine equations often involve methods such as the Euclidean algorithm for finding integer solutions to linear equations, modular arithmetic to reduce complexity, and the method of infinite descent to prove the non-existence of solutions. Unlike general linear equations with real or rational solutions, Diophantine equations require integer solutions, making the problem more restrictive and complex. Advanced approaches include using lattice reduction algorithms and employing bounds derived from number theory to systematically search for all possible integer solutions.
Applications of Linear Equations in Real Life
Linear equations are extensively applied in real-life scenarios such as budgeting, construction, and physics, where relationships between variables need to be modeled and solved to predict outcomes or optimize resources. Unlike Diophantine equations, which seek integer solutions often used in number theory and cryptography, linear equations handle continuous values that model phenomena like supply and demand, electrical circuits, and chemical mixtures. Their versatility in calculating unknowns from known quantities makes them fundamental in engineering, economics, and everyday problem-solving tasks.
Real-World Uses of Diophantine Equations
Diophantine equations, characterized by integer solutions, are essential in cryptography, coding theory, and network design where discrete values are crucial. Unlike linear equations with real-number solutions used in continuous modeling and optimization, Diophantine equations address problems in resource allocation, scheduling, and integer programming in computer science and operations research. Their role in solving integer constraints enhances error detection in digital communications and secure encryption algorithms.
Comparative Analysis: Linear vs. Diophantine Equations
Linear equations represent relationships where variables are raised to the first power and solutions typically reside within real or complex numbers, allowing infinite possible values. Diophantine equations are a specialized subset of linear equations constrained to integer solutions, often requiring more intricate techniques like the Euclidean algorithm or modular arithmetic to resolve feasibility and find particular solutions. The critical contrast lies in solution domains: linear equations focus on continuous spectra, while Diophantine equations emphasize discrete, integral solutions, impacting complexity and application scope.
Conclusion: Choosing the Right Approach
Selecting the appropriate method depends on the nature of the problem: linear equations typically involve continuous variables and standard algebraic techniques, while Diophantine equations require integer solutions and specialized number theory strategies. Understanding the underlying constraints guides whether to apply linear algebra methods or integer-based algorithms such as the Euclidean algorithm or modular arithmetic. Clear identification of solution domains ensures efficient problem-solving in fields like cryptography, coding theory, and combinatorics.
Linear equation Infographic
 libterm.com
libterm.com