Number theory explores the properties and relationships of integers, encompassing prime numbers, divisibility, and modular arithmetic. This branch of mathematics plays a crucial role in cryptography, computer science, and solving complex equations. Dive into the rest of the article to uncover how number theory impacts your daily life and technological advancements.
Table of Comparison
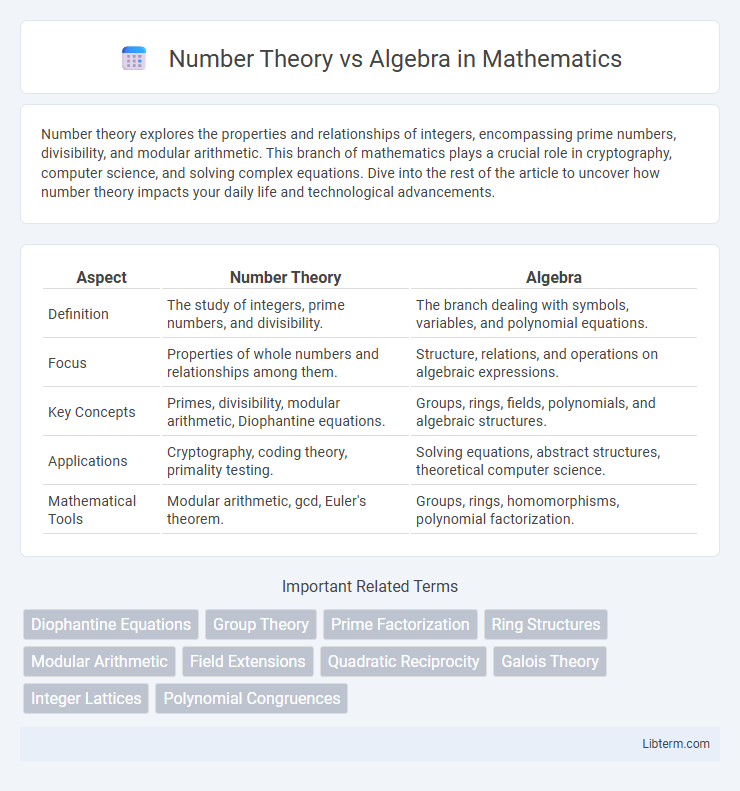
| Aspect | Number Theory | Algebra |
|---|---|---|
| Definition | The study of integers, prime numbers, and divisibility. | The branch dealing with symbols, variables, and polynomial equations. |
| Focus | Properties of whole numbers and relationships among them. | Structure, relations, and operations on algebraic expressions. |
| Key Concepts | Primes, divisibility, modular arithmetic, Diophantine equations. | Groups, rings, fields, polynomials, and algebraic structures. |
| Applications | Cryptography, coding theory, primality testing. | Solving equations, abstract structures, theoretical computer science. |
| Mathematical Tools | Modular arithmetic, gcd, Euler's theorem. | Groups, rings, homomorphisms, polynomial factorization. |
Introduction to Number Theory and Algebra
Number Theory explores properties and relationships of integers, including prime factorization, divisibility, and modular arithmetic, forming a foundation for cryptography and coding theory. Algebra studies symbols and rules for manipulating these symbols, focusing on structures like groups, rings, and fields to solve equations and understand polynomial behavior. Both fields intersect in areas such as algebraic number theory, which applies algebraic methods to solve number-theoretic problems.
Fundamental Concepts in Number Theory
Number theory centers on the properties and relationships of integers, such as divisibility, prime numbers, greatest common divisors, and modular arithmetic. Fundamental concepts include the study of prime factorization, congruences, the Euclidean algorithm, and the distribution of primes. These core elements differentiate number theory from algebra, which primarily explores abstract structures like groups, rings, and fields.
Core Principles of Algebra
Algebra centers on manipulating symbols and solving equations through operations like addition, subtraction, multiplication, and division, providing a framework to express mathematical relationships abstractly. Core principles include understanding variables, functions, and algebraic structures such as groups, rings, and fields that govern the behavior of elements under specific operations. These foundational concepts enable the formulation and resolution of complex problems across diverse mathematical and applied disciplines.
Historical Development of Number Theory and Algebra
Number theory traces its origins to ancient civilizations such as the Babylonians and Greeks, with pivotal contributions from Euclid and Diophantus, while algebra evolved primarily through the works of Persian mathematician Al-Khwarizmi in the 9th century, who formalized systematic solutions for equations. The historical development of number theory advanced significantly with Fermat's Last Theorem and Euler's contributions, whereas algebra expanded during the Renaissance through the symbolic notation introduced by Viete and Descartes. Both disciplines intertwined over centuries, with number theory often considered a subset of algebra under modern abstract algebra frameworks like groups, rings, and fields.
Key Differences Between Number Theory and Algebra
Number theory primarily studies the properties and relationships of integers, including prime numbers, divisibility, and modular arithmetic, while algebra focuses on manipulating symbols and solving equations involving variables across various structures such as groups, rings, and fields. Number theory often deals with discrete structures and specific numerical results, whereas algebra provides a more general framework for abstract mathematical concepts and structural analysis. Key distinctions include number theory's emphasis on the inherent properties of numbers and algebra's focus on operations and transformations within mathematical systems.
Overlapping Areas and Connections
Number theory and algebra intersect significantly in areas such as group theory, ring theory, and field theory, where algebraic structures help solve number-theoretic problems. Concepts like modular arithmetic, Diophantine equations, and algebraic number fields exemplify this overlap, utilizing tools from both disciplines to analyze integers and their properties. These connections enable deeper insights into prime distribution, factorization, and cryptographic algorithms grounded in arithmetic and algebraic frameworks.
Applications of Number Theory in Modern Mathematics
Number theory plays a crucial role in cryptography, enabling secure communication through encryption algorithms like RSA, which rely on properties of prime numbers and modular arithmetic. It also supports error detection and correction in coding theory, essential for data transmission and storage reliability. These applications demonstrate number theory's foundational importance in modern computational and information systems.
Algebraic Structures and Their Uses
Algebraic structures such as groups, rings, and fields form the foundation of abstract algebra, enabling the exploration of mathematical systems through operations and axioms. These structures are pivotal in solving polynomial equations, cryptographic algorithms, and coding theory, providing a framework for understanding symmetry, modular arithmetic, and factorization. In contrast, number theory often employs these algebraic tools to analyze integers, prime distributions, and Diophantine equations, highlighting the interplay between algebraic structures and arithmetic properties.
Challenges and Open Problems in Both Fields
Number theory and algebra both present significant challenges, with number theory grappling with problems such as the distribution of prime numbers and the Riemann Hypothesis, while algebra faces open questions in understanding polynomial equation solutions and group classification. Deep connections exist between the two fields, especially in areas like algebraic number theory, where the structures of algebraic objects illuminate number-theoretic problems. Advances in computational methods have propelled research, yet fundamental open problems like the Birch and Swinnerton-Dyer Conjecture in number theory and the classification of finite simple groups in algebra remain unresolved.
Future Trends in Number Theory and Algebra
Future trends in number theory emphasize advancements in quantum cryptography, leveraging prime factorization and elliptic curves to enhance data security. Algebra is evolving towards higher-dimensional structures and category theory to solve complex problems in topology and theoretical physics. Integration of artificial intelligence accelerates research in both fields, enabling discovery of novel algebraic patterns and number-theoretic algorithms.
Number Theory Infographic
 libterm.com
libterm.com