Action drives progress by turning ideas into tangible results through decisive steps and focused effort. It empowers you to overcome obstacles and achieve goals by maintaining momentum and commitment. Discover how taking effective action can transform your aspirations in the full article ahead.
Table of Comparison
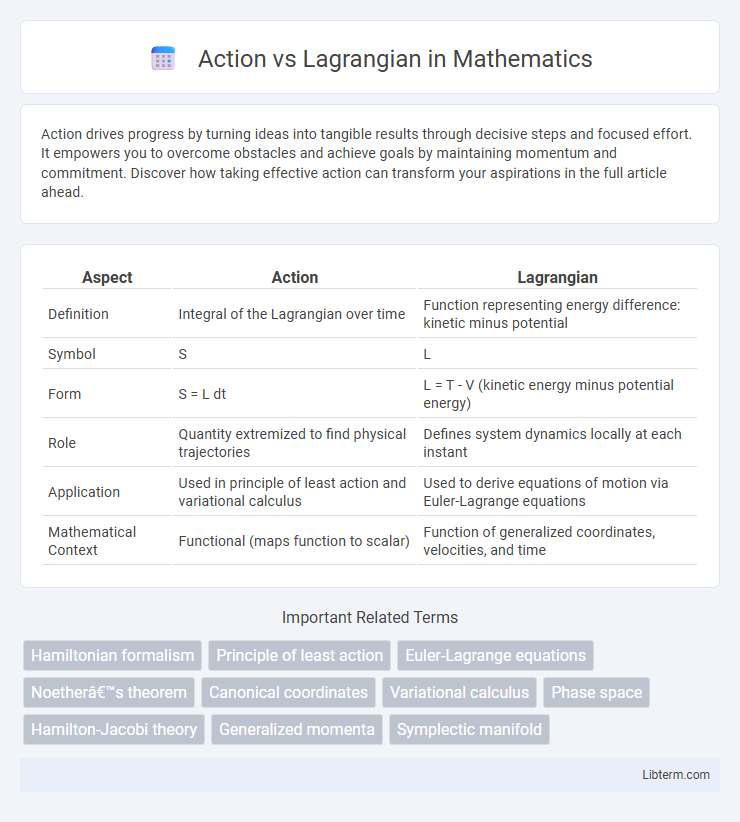
| Aspect | Action | Lagrangian |
|---|---|---|
| Definition | Integral of the Lagrangian over time | Function representing energy difference: kinetic minus potential |
| Symbol | S | L |
| Form | S = L dt | L = T - V (kinetic energy minus potential energy) |
| Role | Quantity extremized to find physical trajectories | Defines system dynamics locally at each instant |
| Application | Used in principle of least action and variational calculus | Used to derive equations of motion via Euler-Lagrange equations |
| Mathematical Context | Functional (maps function to scalar) | Function of generalized coordinates, velocities, and time |
Introduction to Action and Lagrangian
The action is a scalar quantity defined as the integral of the Lagrangian over time, providing a central principle in classical mechanics for deriving equations of motion. The Lagrangian, typically expressed as the difference between kinetic and potential energy (L = T - V), serves as the integrand whose extremization leads to the Euler-Lagrange equations. By minimizing the action, the path taken by a physical system is determined, embodying the principle of least action fundamental to variational mechanics.
Historical Development of Variational Principles
The historical development of variational principles began with Euler and Lagrange's formalization of the principle of least action, which established the foundation for describing physical systems through stationary action functionals. Hamilton extended this framework by introducing the Hamiltonian and reformulating mechanics in terms of the action, leading to the Hamiltonian action principle that unified classical dynamics. These advancements paved the way for modern theoretical physics, linking classical mechanics, quantum mechanics, and field theory through a variational approach.
Fundamental Definitions: Action and Lagrangian
The Action is a scalar quantity defined as the time integral of the Lagrangian, representing the dynamics of a physical system by encapsulating its entire trajectory. The Lagrangian, expressed as L = T - V, is the difference between the kinetic energy (T) and potential energy (V), serving as the core function in Lagrangian mechanics. Minimizing the Action through the principle of least action yields the Euler-Lagrange equations, which govern the system's equations of motion.
The Role of Symmetry in Action and Lagrangian
Symmetry plays a crucial role in both the action and the Lagrangian formalism by dictating conservation laws through Noether's theorem. Invariance of the action under continuous symmetries leads to conserved quantities such as energy, momentum, and angular momentum, directly influencing the form of the Lagrangian. The symmetry properties embedded in the Lagrangian guide the equations of motion, ensuring physical laws remain consistent across transformations.
Euler–Lagrange Equations: Connecting Action and Dynamics
The Euler-Lagrange equations form the cornerstone connecting the Principle of Least Action and the dynamics of a system by providing differential equations that describe motion derived from the Lagrangian function, which encapsulates kinetic and potential energy. Through the variation of the action integral, defined as the integral of the Lagrangian over time, these equations reveal the path a physical system takes to minimize action, leading to equations of motion consistent with Newtonian mechanics. This formalism not only unites classical mechanics under a variational principle but also extends to modern physics frameworks such as quantum mechanics and field theory.
Physical Interpretation of the Lagrangian
The Lagrangian, defined as the difference between kinetic and potential energy (L = T - V), serves as a scalar function that encapsulates the dynamic behavior of a system by describing how energy is distributed and transformed over time. Its physical interpretation centers on the principle of least action, where the actual trajectory of a system minimizes the action integral, linking the Lagrangian to the natural path dictated by underlying forces. This contrasts with the Action itself, which represents the integral of the Lagrangian over time, quantifying the cumulative effect of motion and enabling the derivation of Euler-Lagrange equations governing system evolution.
Applications in Classical Mechanics
The Action principle, defined as the integral of the Lagrangian over time, serves as a foundational concept in classical mechanics for deriving equations of motion via the Euler-Lagrange equations. Applications of the Lagrangian formalism include analyzing complex mechanical systems such as pendulums, rigid body dynamics, and celestial mechanics by transforming constraints into generalized coordinates. This approach simplifies solving problems involving non-conservative forces and provides deeper insights into conservation laws through symmetries identified by Noether's theorem.
Extensions to Quantum Field Theory
The action principle serves as the foundation for formulating quantum field theories by encoding the dynamics of fields through an integral over the Lagrangian density, which encapsulates kinetic and interaction terms. Extensions to quantum field theory often involve modifying the classical action to include gauge fields, fermionic fields, and supersymmetric components, enabling the description of particle interactions and symmetry breaking. These advanced formulations, such as the path integral approach, quantize fields via the functional integral over all possible field configurations weighted by the exponential of the action, bridging classical mechanics with quantum phenomena.
Differences and Similarities: Action vs Lagrangian
The Action is a scalar quantity defined as the time integral of the Lagrangian, which represents the difference between kinetic and potential energy in a system. Both concepts are central to classical mechanics and analytical dynamics, with the Lagrangian function determining the behavior of a system through the principle of stationary action. While the Lagrangian describes instantaneous system properties, the Action accumulates these effects over time to identify the actual path taken by the system.
Future Directions and Open Questions
Future research on the action versus Lagrangian approach prioritizes the development of quantum field theories that unify gravity with the standard model, addressing discrepancies in high-energy regimes. Investigations into non-local actions and generalized Lagrangians aim to resolve anomalies and incorporate dark matter effects within a consistent theoretical framework. Open questions include the role of boundary terms in action principles and the formulation of action functionals in curved spacetime with higher-order derivatives.
Action Infographic
 libterm.com
libterm.com