PSPACE represents the class of decision problems solvable by a Turing machine using a polynomial amount of memory, regardless of the time taken. It encompasses a wide range of complex problems, including those beyond NP and co-NP, highlighting the significant challenge of memory-bounded computation. Explore the rest of the article to uncover the implications of PSPACE in computational complexity and its impact on your understanding of algorithmic problem-solving.
Table of Comparison
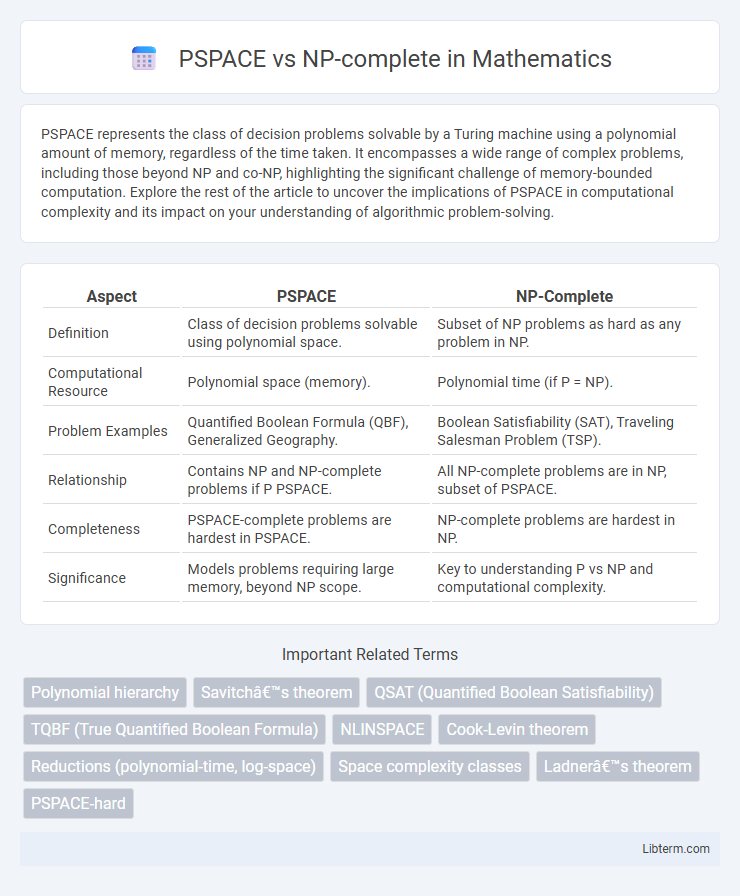
| Aspect | PSPACE | NP-Complete |
|---|---|---|
| Definition | Class of decision problems solvable using polynomial space. | Subset of NP problems as hard as any problem in NP. |
| Computational Resource | Polynomial space (memory). | Polynomial time (if P = NP). |
| Problem Examples | Quantified Boolean Formula (QBF), Generalized Geography. | Boolean Satisfiability (SAT), Traveling Salesman Problem (TSP). |
| Relationship | Contains NP and NP-complete problems if P PSPACE. | All NP-complete problems are in NP, subset of PSPACE. |
| Completeness | PSPACE-complete problems are hardest in PSPACE. | NP-complete problems are hardest in NP. |
| Significance | Models problems requiring large memory, beyond NP scope. | Key to understanding P vs NP and computational complexity. |
Introduction to Complexity Classes
PSPACE encompasses decision problems solvable by a Turing machine using polynomial space, capturing a broader class than NP-complete problems, which are solvable in nondeterministic polynomial time. NP-complete problems are the hardest in NP, meaning every problem in NP reduces to them in polynomial time, while PSPACE includes all problems solvable with polynomial memory regardless of time constraints. Understanding the relationship highlights that NP is contained within PSPACE, but whether PSPACE equals NP-complete remains a central open question in computational complexity theory.
Defining PSPACE: Scope and Significance
PSPACE encompasses all decision problems solvable by a Turing machine using a polynomial amount of memory space, regardless of time constraints, highlighting its broader scope compared to NP-complete problems. NP-complete problems are a subset of NP for which solutions can be verified in polynomial time and are believed to reside within PSPACE, but the equivalence between PSPACE and NP remains an open question. The significance of PSPACE lies in its ability to capture a wide range of complex computational tasks, including games, logic, and quantified Boolean formulas, reflecting the depth of resource limitations beyond mere time.
Understanding NP-complete Problems
NP-complete problems are a class of decision problems that are both in NP and as hard as any problem in NP, meaning every problem in NP can be reduced to them in polynomial time. PSPACE contains all problems solvable with a polynomial amount of memory, including NP and NP-complete problems, indicating PSPACE is a potentially larger complexity class. Understanding NP-complete problems involves recognizing their role as the hardest problems in NP, serving as benchmarks for computational intractability and guiding research on efficient algorithms and complexity theory.
Key Differences Between PSPACE and NP-complete
PSPACE encompasses decision problems solvable using polynomial space, regardless of time, while NP-complete problems require nondeterministic polynomial time verification and are the hardest problems within NP. Unlike NP-complete problems, all PSPACE problems may involve solving games or puzzles with polynomial memory but potentially exponential time, highlighting a broader complexity class. The key distinction lies in resource constraints: NP-complete problems focus on time-bound verification, whereas PSPACE centers on space-bound computation.
Relationships and Containment: PSPACE ⊇ NP-complete
PSPACE, representing problems solvable using polynomial space, strictly contains all NP-complete problems, indicating PSPACE NP-complete. While NP-complete problems are verifiable in polynomial time, PSPACE includes problems potentially requiring more complex strategies but still constrained by polynomial space. This containment reflects the broader computational power of PSPACE compared to NP-complete, though whether these classes are equal or strictly separated remains an open question in complexity theory.
Famous Examples of PSPACE Problems
Famous examples of PSPACE problems include the Quantified Boolean Formula (QBF) problem and various games like Generalized Geography and Hex, which require polynomial space but are believed to be harder than NP-complete problems. Unlike NP-complete problems solvable in nondeterministic polynomial time, PSPACE problems can involve multiple rounds of quantifiers and interleaved choices, making them significantly more complex. The distinction highlights the broader challenge of solving PSPACE problems efficiently compared to the classic NP-complete class.
Notable NP-complete Problems in Practice
Notable NP-complete problems such as the Traveling Salesman Problem, Boolean Satisfiability Problem (SAT), and Graph Coloring showcase significant practical challenges in optimization, verification, and resource allocation. These problems are characterized by their solution spaces that grow exponentially, making them computationally intensive and pivotal in complexity theory. PSPACE, involving problems solvable with polynomial space regardless of time, often encompasses even more complex decision problems than NP-complete, highlighting a critical distinction in computational resource requirements.
Reduction Techniques: PSPACE-complete vs NP-complete
Reduction techniques for PSPACE-complete problems often involve polynomial space reductions that preserve the problem's inherent complexity, highlighting transformations through quantified Boolean formulas or game-like decision processes. NP-complete reductions typically use polynomial-time many-one reductions aiming to convert a known NP-complete problem to another in polynomial time, focusing on satisfiability and combinatorial decision structures. These distinct reduction frameworks underscore the broader computational complexity scope of PSPACE, encompassing problems beyond the NP-complete class.
Open Questions and Major Conjectures
PSPACE vs NP-complete remains a central open question in computational complexity theory, with the major conjecture that PSPACE strictly contains NP-complete, implying problems solvable with polynomial space are potentially harder than NP-complete problems. The open problem whether NP-complete problems can be solved in polynomial space with non-deterministic polynomial time remains unresolved, reflecting the complexity relationship between time-bounded and space-bounded classes. Major conjectures such as PSPACE NP-complete guide research on the boundaries of efficient computation and the inherent difficulty of decision problems.
Real-world Implications and Future Directions
PSPACE problems, characterized by requiring polynomial space, encompass NP-complete problems, which are solvable in nondeterministic polynomial time, highlighting a hierarchy in computational complexity with significant real-world implications for cryptography and optimization. Real-world applications often grapple with NP-complete problems such as scheduling and resource allocation, where efficient algorithms are crucial but remain elusive, pushing research toward approximation and heuristic methods. Future directions include exploring quantum computing's potential to tackle PSPACE challenges and developing algorithms that bridge the gap between theoretical complexity classes and practical problem-solving.
PSPACE Infographic
 libterm.com
libterm.com