Cohomology groups are fundamental tools in algebraic topology that classify and measure the global properties of spaces by assigning algebraic invariants. These groups provide valuable insights into the structure of topological spaces, enabling the study of features such as holes, twists, and other complex characteristics. Explore the rest of the article to deepen your understanding of how cohomology groups reveal the hidden geometry of mathematical spaces.
Table of Comparison
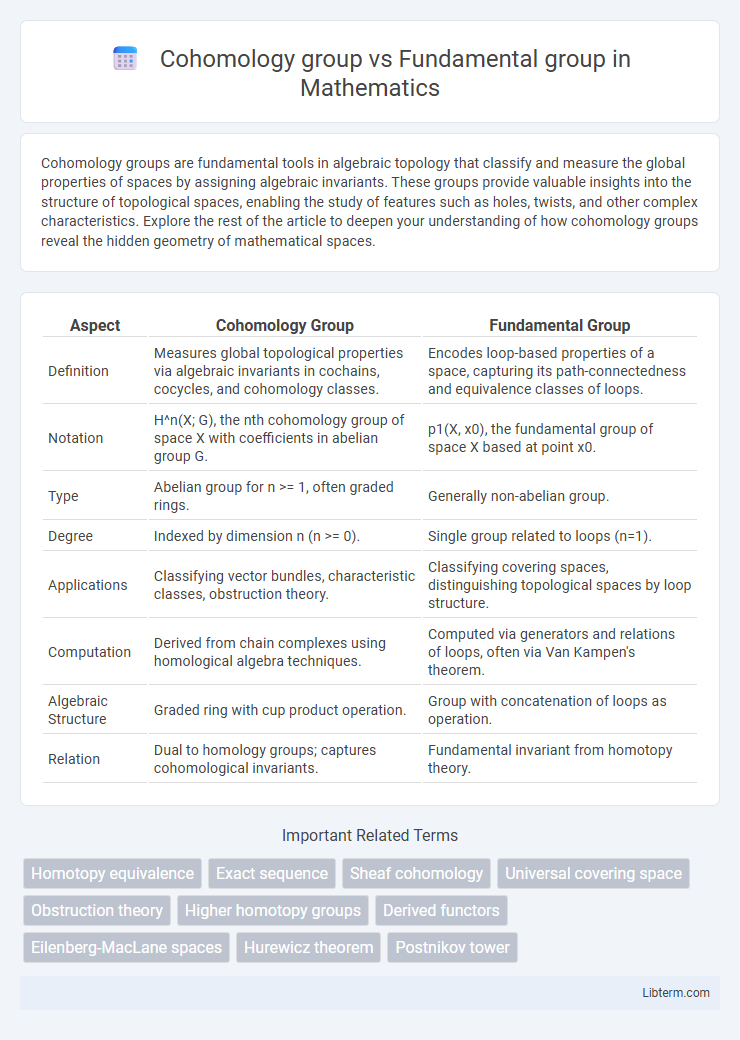
| Aspect | Cohomology Group | Fundamental Group |
|---|---|---|
| Definition | Measures global topological properties via algebraic invariants in cochains, cocycles, and cohomology classes. | Encodes loop-based properties of a space, capturing its path-connectedness and equivalence classes of loops. |
| Notation | H^n(X; G), the nth cohomology group of space X with coefficients in abelian group G. | p1(X, x0), the fundamental group of space X based at point x0. |
| Type | Abelian group for n >= 1, often graded rings. | Generally non-abelian group. |
| Degree | Indexed by dimension n (n >= 0). | Single group related to loops (n=1). |
| Applications | Classifying vector bundles, characteristic classes, obstruction theory. | Classifying covering spaces, distinguishing topological spaces by loop structure. |
| Computation | Derived from chain complexes using homological algebra techniques. | Computed via generators and relations of loops, often via Van Kampen's theorem. |
| Algebraic Structure | Graded ring with cup product operation. | Group with concatenation of loops as operation. |
| Relation | Dual to homology groups; captures cohomological invariants. | Fundamental invariant from homotopy theory. |
Introduction to Cohomology and Fundamental Groups
Fundamental groups classify topological spaces based on loop structures, capturing basic information about their shape and connectivity. Cohomology groups extend this framework by using algebraic tools to measure holes of different dimensions, providing deeper invariants beyond those detected by the fundamental group. Together, these groups offer complementary perspectives in algebraic topology, with the fundamental group focusing on 1-dimensional loops and cohomology groups analyzing higher-dimensional structures through chain complexes and homological algebra.
Defining the Fundamental Group
The fundamental group, denoted p1(X, x0), is defined as the set of equivalence classes of based loops in a topological space X, with equivalence given by homotopy relative to the base point x0. This group captures information about the space's 1-dimensional hole structure and path-connectedness, serving as a powerful algebraic invariant in algebraic topology. In contrast, cohomology groups consist of higher-dimensional algebraic structures derived from cochains, measures of global topological features beyond just loops.
Understanding Cohomology Groups
Cohomology groups provide algebraic invariants that classify topological spaces by capturing global properties through cochains, coboundaries, and cocycles, enriching the information obtained from fundamental groups which mainly detect loop structures and path-connectedness. Unlike the fundamental group p1(X) that measures how loops in a space X fail to contract, cohomology groups Hn(X; G) use contravariant functors to study n-dimensional holes and obstructions via homological algebra techniques. Understanding cohomology groups involves analyzing their ring and module structures, enabling deeper insights into manifold properties, characteristic classes, and dualities absent in traditional homotopy group frameworks.
Key Differences Between Cohomology and Fundamental Groups
Cohomology groups classify topological spaces using algebraic invariants derived from differential forms or cochains, providing information about global properties such as holes and obstructions in various dimensions. Fundamental groups focus on the classification of loops based at a point, capturing the space's basic shape and path-connectedness through elements representing homotopy classes of loops. Unlike the non-abelian fundamental group, cohomology groups are abelian, enabling richer algebraic structures like cup products that encode additional geometric and topological information.
Topological Significance: Homotopy vs Homology
The fundamental group captures the topological structure of a space by classifying loops up to homotopy, reflecting the space's path-connectedness and higher-dimensional holes through homotopy equivalence. In contrast, cohomology groups measure global properties via homology classes, detecting features like holes and voids by analyzing cycles and boundaries in algebraic topology. Together, the fundamental and cohomology groups provide complementary invariants: the fundamental group encodes homotopy-based loop information, while cohomology groups characterize homological structures and algebraic invariants of the space.
Algebraic Structures in Cohomology and Fundamental Groups
The cohomology group is an algebraic structure defined by abelian groups that classify topological spaces through cochains, cocycles, and coboundaries, revealing higher-dimensional holes and invariants. In contrast, the fundamental group is a non-abelian group capturing information about loops and path homotopy classes based at a point, primarily encoding one-dimensional holes. Cohomology groups often possess ring structures via the cup product, enabling rich algebraic operations, while the fundamental group's group operations reflect concatenation of loops and serve as a foundational tool in algebraic topology.
Computation Methods and Techniques
Computing the fundamental group often involves combinatorial techniques such as van Kampen's theorem, which breaks a topological space into simpler parts to analyze loop-based structures, whereas cohomology groups are typically computed using chain complexes and derived functor methods like singular or Cech cohomology. Fundamental group calculations rely heavily on generators and relations derived from paths, while cohomology computations employ algebraic tools including exact sequences and spectral sequences to extract invariants from differential graded algebras. Algorithms for fundamental group determination are less automated and more geometric, contrasted with systematic, algebraic approaches for cohomology that benefit from computational algebra systems and homological algebra frameworks.
Applications in Topology and Geometry
Cohomology groups provide powerful algebraic invariants that classify topological spaces by capturing global geometric structures and detecting holes of various dimensions, essential for studying fiber bundles and characteristic classes. Fundamental groups encode the space's loop structures, revealing information about path-connectedness and coverings crucial for analyzing manifolds and complex algebraic varieties. Together, cohomology and fundamental groups facilitate the classification of surfaces, enable the calculation of Betti numbers, and underpin key results in geometric topology such as the Hurewicz theorem and Poincare duality.
Interactions and Relationships Between the Groups
Cohomology groups and the fundamental group both capture essential topological information but operate at different algebraic levels, with the fundamental group encoding loops and path-connectedness while cohomology groups classify higher-dimensional structures like holes and voids. The relationship between these groups often emerges through the Hurewicz theorem, which connects the abelianization of the fundamental group to the first homology group, dual to the first cohomology group. Additionally, cohomology theories with coefficients in various modules can reflect representations of the fundamental group, highlighting deeper interactions in algebraic topology.
Summary and Future Directions in Group Theory
Cohomology groups and fundamental groups serve distinct yet complementary roles in algebraic topology, with cohomology groups providing algebraic invariants that capture global topological properties and fundamental groups encoding the space's loop structures. Advances in group theory reveal promising intersections, such as using cohomological methods to classify fundamental groups of complex spaces or exploring higher-dimensional analogs through homotopy group generalizations. Future research emphasizes developing computational tools for these groups, investigating their applications in higher category theory, and uncovering deeper connections between geometric structures and algebraic invariants.
Cohomology group Infographic
 libterm.com
libterm.com