A class group serves as an essential platform for students and teachers to collaborate, share resources, and communicate effectively. It enhances learning by enabling quick access to important announcements, study materials, and peer support. Explore the rest of the article to discover how your involvement in a class group can boost academic success.
Table of Comparison
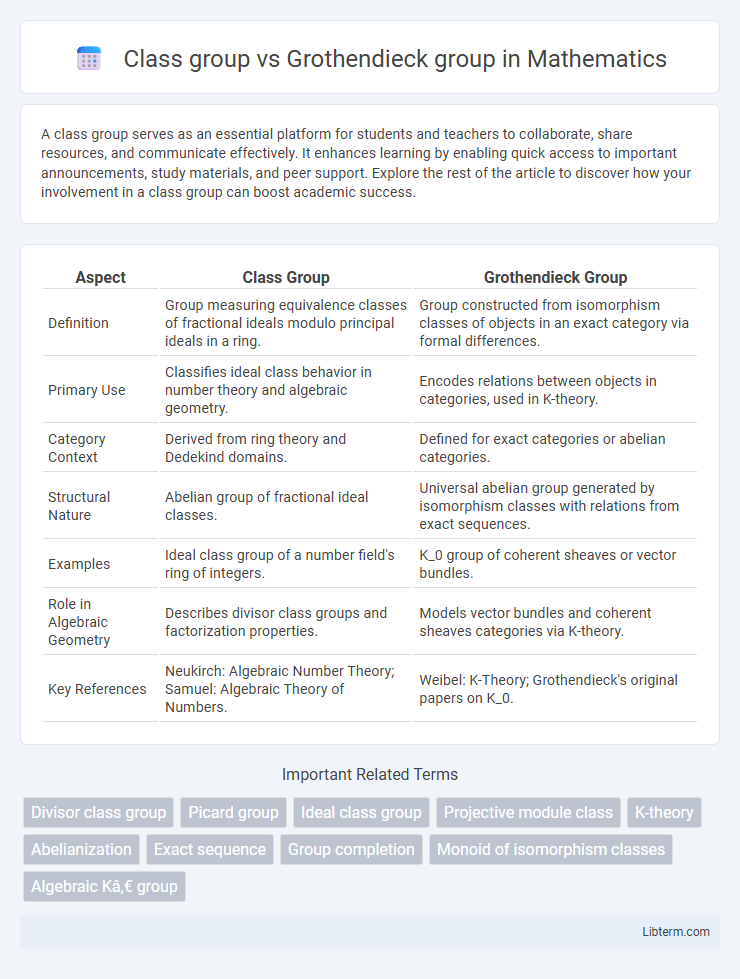
| Aspect | Class Group | Grothendieck Group |
|---|---|---|
| Definition | Group measuring equivalence classes of fractional ideals modulo principal ideals in a ring. | Group constructed from isomorphism classes of objects in an exact category via formal differences. |
| Primary Use | Classifies ideal class behavior in number theory and algebraic geometry. | Encodes relations between objects in categories, used in K-theory. |
| Category Context | Derived from ring theory and Dedekind domains. | Defined for exact categories or abelian categories. |
| Structural Nature | Abelian group of fractional ideal classes. | Universal abelian group generated by isomorphism classes with relations from exact sequences. |
| Examples | Ideal class group of a number field's ring of integers. | K_0 group of coherent sheaves or vector bundles. |
| Role in Algebraic Geometry | Describes divisor class groups and factorization properties. | Models vector bundles and coherent sheaves categories via K-theory. |
| Key References | Neukirch: Algebraic Number Theory; Samuel: Algebraic Theory of Numbers. | Weibel: K-Theory; Grothendieck's original papers on K_0. |
Introduction to Class Groups and Grothendieck Groups
Class groups measure the failure of unique factorization in integral domains by classifying ideal classes modulo principal ideals, providing insights into algebraic number theory and arithmetic geometry. Grothendieck groups generalize this concept by constructing an abelian group from a commutative monoid, typically associated with isomorphism classes of projective modules or vector bundles, capturing essential algebraic and topological invariants. Both concepts play pivotal roles in algebraic K-theory, with class groups focusing on ideal class structures and Grothendieck groups formalizing additive invariants through categorical frameworks.
Defining the Class Group: Structure and Examples
The class group is an algebraic structure that measures the failure of unique factorization in integral domains by classifying fractional ideals modulo principal ideals, forming an abelian group that captures ideal class equivalence. In number theory, the class group of the ring of integers in a number field encodes essential information about its arithmetic properties, with finite class groups indicating unique factorization domains. Examples include the class group of quadratic fields, where a trivial class group implies a unique factorization of integers, while nontrivial class groups reveal more complex ideal structures.
Understanding the Grothendieck Group: Foundations and Applications
The Grothendieck group is a fundamental construction in algebraic K-theory that generalizes the notion of the class group by formally adding inverses to a commutative monoid, enabling the transition from a semigroup of isomorphism classes of objects to an abelian group. It finds crucial applications in algebraic geometry, where it classifies vector bundles, and in number theory, where it refines the classification of projective modules beyond the ideal-theoretic perspective of the class group. By encapsulating equivalence classes with well-defined subtraction, the Grothendieck group provides a robust framework for understanding and manipulating algebraic and geometric invariants.
Historical Development of Class Groups and Grothendieck Groups
Class groups originated in the 19th century through Richard Dedekind's work on algebraic number theory, providing a fundamental tool to measure the failure of unique factorization in rings of integers. Grothendieck groups emerged in the 20th century from Alexander Grothendieck's pioneering efforts in algebraic geometry and homological algebra to generalize the notion of class groups via K-theory, capturing algebraic invariants of categories. The historical trajectory highlights a shift from arithmetic-focused ideals and divisors toward categorical and homological structures that unify and extend classical class group concepts.
Algebraic Structures: Comparing Class Groups and Grothendieck Groups
Class groups and Grothendieck groups are fundamental algebraic structures used to classify and analyze objects up to certain equivalences in algebraic number theory and algebraic geometry. The class group measures the failure of unique factorization in a domain by classifying fractional ideals modulo principal ideals, while the Grothendieck group K_0 abstracts isomorphism classes of projective modules or vector bundles into an abelian group via formal differences. Their comparison highlights the class group's role in arithmetic invariants and the Grothendieck group's universal characterization in K-theory, emphasizing different categorical frameworks and algebraic invariants used to understand module or ideal structures.
Key Differences Between Class Group and Grothendieck Group
The class group primarily measures the failure of unique factorization in a number field or algebraic variety by analyzing fractional ideals modulo principal ideals, capturing divisor-like information. In contrast, the Grothendieck group constructs an abelian group from an exact category by considering isomorphism classes of objects with relations induced by short exact sequences, enabling broader applications in algebraic K-theory. Key differences lie in their foundational purposes: the class group focuses on algebraic number theory and divisor class structures, whereas the Grothendieck group provides a universal additive invariant in category theory and homological algebra.
Roles in Algebraic Geometry and Number Theory
Class groups measure the failure of unique factorization in algebraic number fields and provide key invariants in algebraic number theory. Grothendieck groups serve as universal objects classifying vector bundles or coherent sheaves on schemes, playing a crucial role in algebraic geometry and K-theory. Both groups encode structural information: class groups describe ideal class structure, while Grothendieck groups capture equivalence classes of algebraic objects via exact sequences.
Connections to Module Theory and Category Theory
Class groups capture isomorphism classes of projective modules over a ring, providing invariants in algebraic number theory and algebraic geometry. Grothendieck groups generalize this concept by forming a universal group from exact sequences of modules or objects in an exact category, thereby encoding relations in the module category or abelian category. The interplay between these groups highlights how algebraic K-theory bridges module theory and category theory through the study of projective modules, exact sequences, and categorical equivalences.
Computational Aspects and Challenges
Computing the Class group of a ring involves determining equivalence classes of fractional ideals, often requiring intricate factorization algorithms and heavy algebraic number theory tools, whereas the Grothendieck group construction relies on relations in categories, demanding effective handling of exact sequences and morphism classes. The Class group computation is challenged by intricate ideal class representatives and the need for explicit norm and valuation calculations, while Grothendieck group calculations face difficulties in managing large categories and ensuring well-defined group completions. Efficient algorithms for Class groups leverage algebraic number field data, lattice basis reduction, and ideal class enumeration, contrasting with category-theoretic approaches that require symbolic manipulation of objects and morphisms to construct the Grothendieck group.
Summary: Choosing Between Class Group and Grothendieck Group
The Class group captures the ideal-theoretic structure of a ring by measuring the deviation from unique factorization, crucial for algebraic number theory and algebraic geometry. The Grothendieck group, constructed from exact sequences of objects in an abelian category, encodes more general additive invariants and is fundamental in K-theory and representation theory. Selecting between the Class group and Grothendieck group depends on whether the focus is on ideal class structure or on additive relations among objects in a category.
Class group Infographic
 libterm.com
libterm.com