Axiomatic principles serve as foundational truths in mathematics and logic, providing unquestionable starting points for reasoning and proofs. Understanding these core concepts enables you to grasp complex theories systematically and critically. Explore the rest of the article to discover how axiomatic systems shape various fields of study.
Table of Comparison
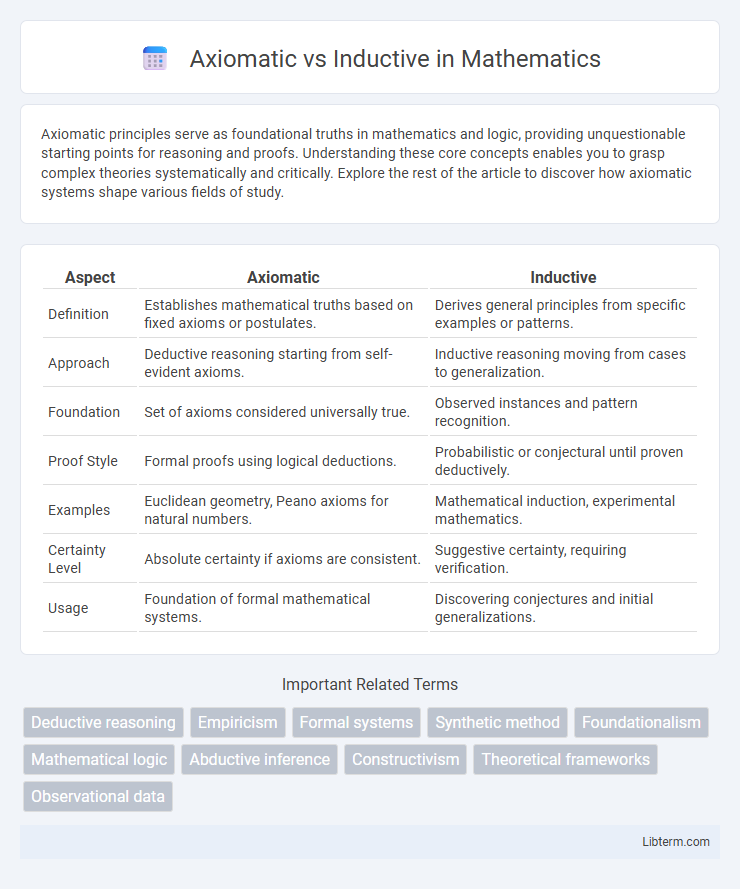
| Aspect | Axiomatic | Inductive |
|---|---|---|
| Definition | Establishes mathematical truths based on fixed axioms or postulates. | Derives general principles from specific examples or patterns. |
| Approach | Deductive reasoning starting from self-evident axioms. | Inductive reasoning moving from cases to generalization. |
| Foundation | Set of axioms considered universally true. | Observed instances and pattern recognition. |
| Proof Style | Formal proofs using logical deductions. | Probabilistic or conjectural until proven deductively. |
| Examples | Euclidean geometry, Peano axioms for natural numbers. | Mathematical induction, experimental mathematics. |
| Certainty Level | Absolute certainty if axioms are consistent. | Suggestive certainty, requiring verification. |
| Usage | Foundation of formal mathematical systems. | Discovering conjectures and initial generalizations. |
Introduction to Axiomatic and Inductive Reasoning
Axiomatic reasoning begins with clearly defined axioms or self-evident truths from which other statements are logically derived, forming a structured and consistent framework essential in fields like mathematics and formal logic. Inductive reasoning, on the other hand, involves drawing generalized conclusions based on specific observations or empirical evidence, widely used in scientific research to formulate hypotheses and theories. Both methods contribute to knowledge development but differ fundamentally in approach: axiomatic relies on deductive logic, while inductive grounds its conclusions in observed patterns.
Defining the Axiomatic Approach
The axiomatic approach establishes a system based on fundamental principles or axioms that are assumed true without proof, serving as the foundation for deriving further theorems and conclusions. This method prioritizes consistency, completeness, and logical deduction within mathematical structures, such as Euclidean geometry or set theory. By defining a clear set of axioms, the axiomatic framework enables rigorous proof construction and systematic knowledge development.
Understanding Inductive Reasoning
Inductive reasoning involves drawing generalized conclusions from specific observations or evidence, allowing for probabilistic but not certain knowledge. Unlike axiomatic reasoning, which starts from self-evident truths or premises to derive conclusions, inductive methods rely on patterns and empirical data to formulate theories. This approach is fundamental in scientific inquiry, where hypotheses are tested and refined based on observed phenomena.
Key Differences Between Axiomatic and Inductive Methods
Axiomatic methods rely on a set of predefined axioms or principles from which conclusions are logically derived, ensuring consistency and certainty in mathematical and logical systems. Inductive methods, in contrast, involve generalizing patterns or rules based on empirical observations and specific examples, emphasizing probabilistic reasoning rather than absolute proof. The key difference lies in axiomatic approaches providing deductive certainty while inductive approaches offer empirical generalizations that remain subject to revision.
Historical Development of Axiomatic and Inductive Logic
The historical development of axiomatic logic began with ancient Greek mathematicians like Euclid, who formalized geometric principles using a fixed set of axioms and rigorous deductive reasoning. Inductive logic evolved later as philosophers like Francis Bacon emphasized empirical observation and the generalization of patterns to form broader conclusions. Both approaches have shaped the foundation of modern scientific methodology, with axiomatic systems providing structured proof frameworks and inductive logic enabling hypothesis generation from experimental data.
Applications of Axiomatic Systems
Axiomatic systems are foundational in mathematics and computer science, providing a rigorous framework for proving theorems and ensuring consistency within abstract structures like geometry and algebra. They enable formal verification in software engineering by establishing clear rules and axioms that guide program correctness and security protocols. In contrast to inductive reasoning, axiomatic methods deliver definitive proofs based on initial axioms, making them indispensable in areas requiring absolute certainty such as logic, cryptography, and formal semantics.
Examples of Inductive Reasoning in Practice
Inductive reasoning involves drawing general conclusions from specific observations, such as noticing that the sun rises every morning and inferring it will rise tomorrow. Scientific research often employs inductive reasoning by collecting experimental data and formulating broader theories, like observing multiple instances of water boiling at 100degC to conclude the boiling point at sea level. Everyday decision-making also reflects inductive reasoning, for example, assuming a restaurant is good based on consistently positive reviews and customer experiences.
Strengths and Limitations of Axiomatic Reasoning
Axiomatic reasoning provides a solid foundation for mathematical and logical systems by relying on clearly defined axioms that ensure consistency and deductive certainty. Its strength lies in producing unequivocal truths and enabling complex theorems to be derived systematically, but it is limited by the dependence on chosen axioms, which may not encompass all real-world phenomena or may lead to incomplete or non-applicable frameworks. Moreover, axiomatic systems can become rigid, making it challenging to incorporate new information that falls outside initial assumptions.
Advantages and Challenges of Inductive Methods
Inductive methods excel in generating new hypotheses by deriving generalized conclusions from specific observations, offering flexibility in exploring complex and dynamic data patterns. These approaches adapt well to real-world scenarios where complete information is unavailable, facilitating innovation in scientific research and machine learning. However, inductive reasoning faces challenges such as potential overgeneralization, susceptibility to bias from incomplete data, and difficulty in guaranteeing absolute certainty compared to axiomatic deductive systems.
Choosing Between Axiomatic and Inductive Approaches
Choosing between axiomatic and inductive approaches depends on the context and goals of the research or analysis. Axiomatic methods rely on well-defined, foundational principles to derive conclusions with certainty, suitable for fields like mathematics and formal logic where precision is paramount. Inductive approaches build generalizations based on empirical observations and data, making them ideal for scientific inquiry and situations requiring hypothesis formation from patterns or trends.
Axiomatic Infographic
 libterm.com
libterm.com