Homology groups are algebraic structures used in topology to measure and classify the features of a geometric object, such as holes of different dimensions. These groups provide a powerful tool for understanding the shape and structure of spaces by capturing essential connectivity information. Dive into the article to explore how homology groups can reveal the hidden properties of your topological spaces.
Table of Comparison
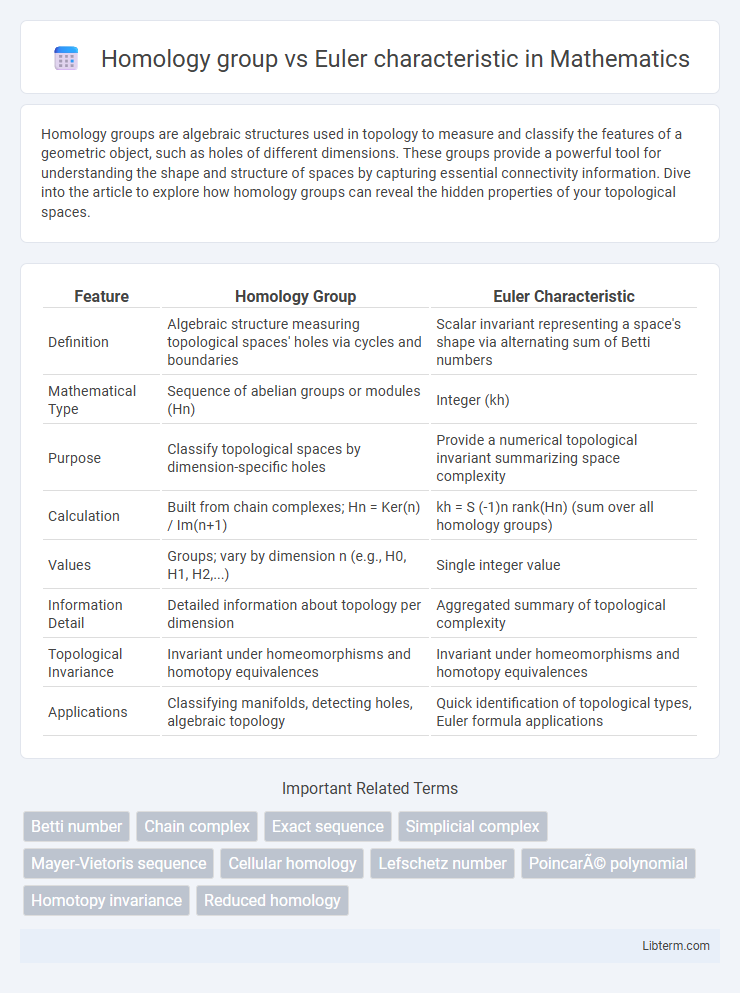
| Feature | Homology Group | Euler Characteristic |
|---|---|---|
| Definition | Algebraic structure measuring topological spaces' holes via cycles and boundaries | Scalar invariant representing a space's shape via alternating sum of Betti numbers |
| Mathematical Type | Sequence of abelian groups or modules (Hn) | Integer (kh) |
| Purpose | Classify topological spaces by dimension-specific holes | Provide a numerical topological invariant summarizing space complexity |
| Calculation | Built from chain complexes; Hn = Ker(n) / Im(n+1) | kh = S (-1)n rank(Hn) (sum over all homology groups) |
| Values | Groups; vary by dimension n (e.g., H0, H1, H2,...) | Single integer value |
| Information Detail | Detailed information about topology per dimension | Aggregated summary of topological complexity |
| Topological Invariance | Invariant under homeomorphisms and homotopy equivalences | Invariant under homeomorphisms and homotopy equivalences |
| Applications | Classifying manifolds, detecting holes, algebraic topology | Quick identification of topological types, Euler formula applications |
Introduction to Homology Groups and Euler Characteristic
Homology groups provide a powerful algebraic tool for analyzing topological spaces by capturing information about cycles and boundaries across different dimensions, enabling the classification of spaces based on their structural features. The Euler characteristic is a topological invariant derived from the alternating sum of the ranks of these homology groups, succinctly summarizing the shape or structure of a space. By linking homology groups to the Euler characteristic, mathematicians gain insight into the fundamental properties of spaces, facilitating deeper understanding in algebraic topology.
Mathematical Foundations of Homology
Homology groups provide algebraic structures that classify topological spaces based on cycles and boundaries, capturing information about holes in different dimensions. The Euler characteristic, defined as the alternating sum of ranks of homology groups, serves as a topological invariant reflecting the space's shape and connectivity. The mathematical foundations of homology rely on chain complexes and exact sequences, enabling computation of homology groups and thereby linking algebraic properties to topological invariants like the Euler characteristic.
Understanding the Euler Characteristic
The Euler characteristic is a topological invariant defined as the alternating sum of the ranks of homology groups, capturing essential information about a space's shape and connectivity. Homology groups quantify the presence of holes across various dimensions, with the Euler characteristic synthesizing this data into a single scalar value. This invariant plays a crucial role in classifying surfaces and complex manifolds by linking algebraic topology to geometric properties.
Historical Development of Homology and Euler Characteristic
The historical development of homology groups began in the early 20th century with pioneers like Henri Poincare, who introduced concepts to classify topological spaces through algebraic invariants. Euler characteristic, initially formulated by Leonhard Euler in the 18th century for polyhedra, later became foundational in topology as a combinatorial invariant linked to homology via Betti numbers. The formalization of homology theory provided a rigorous algebraic framework that deepened the understanding of the Euler characteristic as an alternating sum of ranks of homology groups.
Calculating Homology Groups in Topological Spaces
Calculating homology groups in topological spaces involves analyzing cycles and boundaries within a space to determine its algebraic invariants, which reveal the number of holes of different dimensions. Homology groups are constructed using chain complexes and boundary operators, providing detailed information about the space's structure beyond what the Euler characteristic offers. Unlike the Euler characteristic, which gives a single numeric summary combining ranks of homology groups via alternating sums, homology groups describe the topological space with richer, multi-dimensional algebraic data.
Methods for Computing Euler Characteristic
Computing the Euler characteristic often involves analyzing homology groups by using their ranks, known as Betti numbers, to apply the alternating sum formula kh = S(-1)^i rank(H_i). Techniques such as simplicial homology, cellular homology, and Morse theory provide systematic methods to calculate these homology groups for a topological space. Software tools like computational algebra systems enhance the practical computation of these invariants by automating chain complex reductions and boundary operator calculations.
Relationship Between Homology Groups and Euler Characteristic
The Euler characteristic of a topological space is computed as the alternating sum of the ranks of its homology groups, formally expressed as kh = (-1)^i rank(H_i). Homology groups measure the number of i-dimensional holes, while the Euler characteristic provides a single numerical invariant summarizing these topological features. This relationship allows algebraic topology to connect discrete invariants from homology with a global geometric property like the Euler characteristic.
Applications in Algebraic Topology
Homology groups provide detailed algebraic invariants that classify topological spaces by capturing information about cycles and boundaries at various dimensions. The Euler characteristic serves as a numerical invariant calculated from the alternating sum of the ranks of homology groups, offering a simplified but powerful tool to distinguish topological spaces. Applications in algebraic topology leverage homology groups for detecting holes and connectivity properties, while the Euler characteristic aids in classifying surfaces and analyzing complex structures efficiently.
Examples: Comparing Homology and Euler Characteristic
Homology groups provide detailed algebraic invariants revealing the number and types of holes in a topological space, while the Euler characteristic offers a single integer summarizing the space's shape complexity. For example, a torus has homology groups H_0 Z, H_1 Z2, and H_2 Z reflecting one connected component, two independent loops, and one void, resulting in an Euler characteristic kh = 0. In contrast, a sphere has homology groups H_0 Z, H_1 = 0, H_2 Z and an Euler characteristic kh = 2, highlighting fewer holes and simpler topology.
Summary: Key Differences and Connections
Homology groups classify topological spaces by measuring cycles and boundaries in various dimensions, providing algebraic invariants that capture holes of different types. The Euler characteristic is a single number computed as an alternating sum of the ranks of these homology groups, summarizing the overall shape complexity succinctly. While homology groups offer detailed structural information, the Euler characteristic condenses this data into a scalar invariant useful for distinguishing broad topological properties.
Homology group Infographic
 libterm.com
libterm.com