Eulerian graphs represent a class of graphs where a path exists that visits every edge exactly once, a concept critical in solving routing and network problems. Understanding Eulerian circuits can enhance your ability to optimize routes in logistics, computer networks, and circuit designs. Explore the following article to discover how Eulerian principles apply to real-world challenges and improve your problem-solving skills.
Table of Comparison
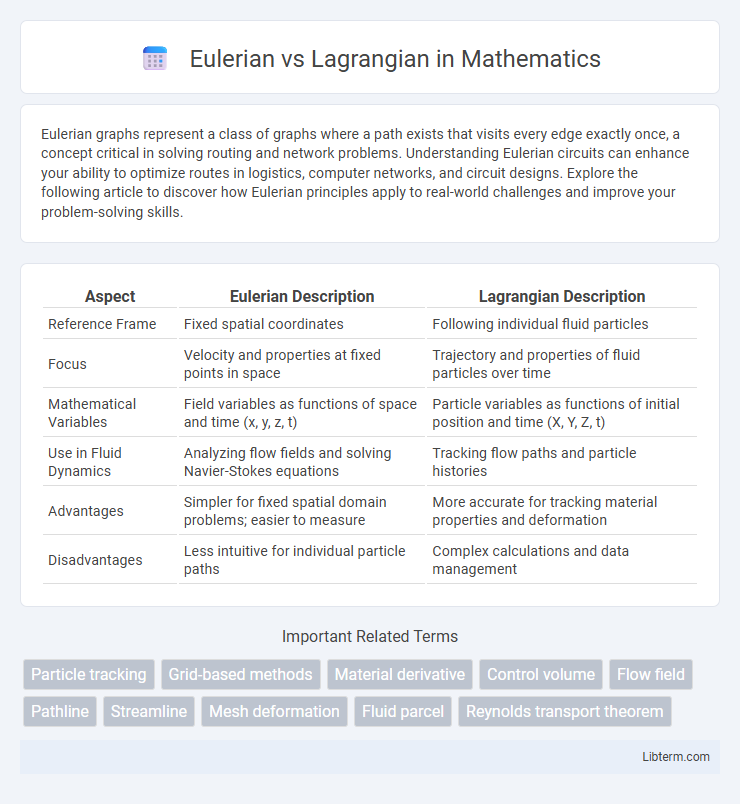
| Aspect | Eulerian Description | Lagrangian Description |
|---|---|---|
| Reference Frame | Fixed spatial coordinates | Following individual fluid particles |
| Focus | Velocity and properties at fixed points in space | Trajectory and properties of fluid particles over time |
| Mathematical Variables | Field variables as functions of space and time (x, y, z, t) | Particle variables as functions of initial position and time (X, Y, Z, t) |
| Use in Fluid Dynamics | Analyzing flow fields and solving Navier-Stokes equations | Tracking flow paths and particle histories |
| Advantages | Simpler for fixed spatial domain problems; easier to measure | More accurate for tracking material properties and deformation |
| Disadvantages | Less intuitive for individual particle paths | Complex calculations and data management |
Introduction to Eulerian and Lagrangian Approaches
The Eulerian approach analyzes fluid flow by examining changes at fixed spatial points, capturing velocity and pressure fields over time. The Lagrangian method tracks individual fluid particles as they move through space, providing detailed trajectories and deformation patterns. Both approaches offer complementary perspectives essential for computational fluid dynamics and advanced flow analysis.
Fundamental Concepts: Eulerian Perspective
The Eulerian perspective in fluid dynamics analyzes flow properties at fixed points in space as the fluid passes through, emphasizing velocity, pressure, and density fields as functions of time and position. This approach contrasts with tracking individual fluid particles, enabling a detailed examination of spatial variations and temporal changes in the flow. Eulerian methods are fundamental in computational fluid dynamics (CFD) for solving Navier-Stokes equations on fixed grids.
Fundamental Concepts: Lagrangian Perspective
The Lagrangian perspective in fluid dynamics tracks individual fluid particles as they move through space and time, focusing on their trajectories and properties. This approach provides detailed information on particle paths, velocities, and accelerations by observing changes from the particle's initial position. It contrasts with the Eulerian framework, which analyzes fluid properties at fixed spatial locations rather than following the particles themselves.
Mathematical Frameworks and Notation
Eulerian frameworks analyze fluid flow by observing changes at fixed points in space, using partial derivatives with respect to time and spatial coordinates, represented as \(\frac{\partial \mathbf{u}}{\partial t} + (\mathbf{u} \cdot \nabla) \mathbf{u}\). Lagrangian approaches track individual fluid particles, employing total derivatives \( \frac{D}{Dt} \) that follow particle trajectories and describe their evolving properties. These distinct notations underpin the mathematical modeling of fluid dynamics, influencing computational methods and physical interpretations within continuum mechanics.
Applications in Fluid Dynamics
Eulerian methods analyze fluid flow by observing changes at fixed points in space, making them ideal for simulating large-scale atmospheric patterns and ocean currents. Lagrangian approaches track individual fluid particles, offering precise insights into pollutant dispersion, particle transport, and multiphase flows in engineering systems. These complementary techniques enhance understanding and prediction in computational fluid dynamics, environmental studies, and aerospace engineering.
Advantages of Eulerian Methods
Eulerian methods excel in analyzing fluid flow by fixing the spatial frame of reference, enabling detailed observation of velocity and pressure fields at specific points. These methods handle complex boundary conditions and turbulent flow patterns more efficiently, making them ideal for computational fluid dynamics simulations. Their fixed-grid approach simplifies mathematical modeling and enhances the accuracy of flow predictions in engineering applications.
Strengths of Lagrangian Techniques
Lagrangian techniques excel in tracking individual particle trajectories, enabling precise modeling of fluid flow and transport phenomena at a granular level. These methods allow for detailed analysis of deformation, mixing, and interface dynamics in complex systems such as multiphase flows or pollutant dispersion. Computational frameworks like Smoothed Particle Hydrodynamics (SPH) leverage Lagrangian strengths to simulate highly nonlinear, transient behaviors with improved accuracy over Eulerian counterparts.
Key Differences and Comparative Analysis
The Eulerian approach analyzes fluid flow by observing specific locations in the space through which the fluid moves, focusing on changes in velocity and other properties at fixed points. In contrast, the Lagrangian method tracks individual fluid particles as they move, providing insights into particle trajectories and history-dependent phenomena. Comparing both, Eulerian models are computationally efficient for steady-state problems, while Lagrangian frameworks excel in capturing transient behaviors and detailed path-dependent dynamics.
Challenges and Limitations of Each Approach
Eulerian methods face challenges in accurately tracking interfaces and boundaries, especially in highly deformable flows, due to their fixed spatial grid. Lagrangian approaches struggle with computational complexity and numerical instability when dealing with large deformations or complex topologies, as particles can cluster or disperse unevenly. Both methods exhibit limitations in capturing multiscale phenomena and require sophisticated numerical techniques to balance accuracy and efficiency.
Choosing the Right Framework: Practical Considerations
Selecting between Eulerian and Lagrangian frameworks hinges on the specific application and data requirements. Eulerian methods excel in fixed spatial analyses such as fluid flow fields, offering straightforward measurement of velocity and pressure at set points. Lagrangian approaches are advantageous for tracking individual particle trajectories and understanding dynamic histories in complex, moving systems.
Eulerian Infographic
 libterm.com
libterm.com