Taylor series provide a powerful method to approximate complex functions using infinite sums of derivatives at a single point, enabling simpler computation in various fields like physics, engineering, and computer science. These series help transform nonlinear problems into manageable polynomial forms, making analysis and problem-solving more accessible. Explore the rest of the article to understand how you can apply Taylor series for accurate function approximations and practical solutions.
Table of Comparison
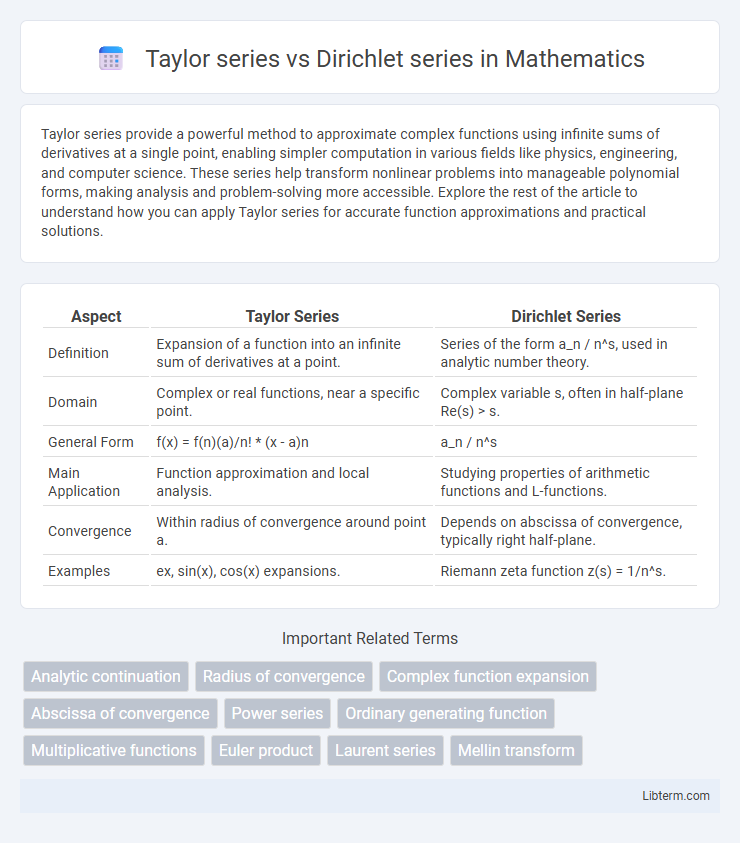
| Aspect | Taylor Series | Dirichlet Series |
|---|---|---|
| Definition | Expansion of a function into an infinite sum of derivatives at a point. | Series of the form a_n / n^s, used in analytic number theory. |
| Domain | Complex or real functions, near a specific point. | Complex variable s, often in half-plane Re(s) > s. |
| General Form | f(x) = f(n)(a)/n! * (x - a)n | a_n / n^s |
| Main Application | Function approximation and local analysis. | Studying properties of arithmetic functions and L-functions. |
| Convergence | Within radius of convergence around point a. | Depends on abscissa of convergence, typically right half-plane. |
| Examples | ex, sin(x), cos(x) expansions. | Riemann zeta function z(s) = 1/n^s. |
Introduction to Taylor Series and Dirichlet Series
Taylor series represent functions as infinite sums of polynomial terms derived from function derivatives at a single point, typically used for analytic functions around that point. Dirichlet series, often expressed as an infinite sum of terms a_n / n^s, are fundamental in number theory and complex analysis, particularly in studying L-functions and the Riemann zeta function. While Taylor series expand functions locally in the complex plane, Dirichlet series encode arithmetic information globally through their coefficients and complex variable exponents.
Fundamental Definitions
Taylor series represent functions as infinite sums of their derivatives evaluated at a single point, typically expressed as \( f(x) = \sum_{n=0}^\infty \frac{f^{(n)}(a)}{n!}(x - a)^n \), capturing local analytic behavior. Dirichlet series are infinite sums of the form \( \sum_{n=1}^\infty \frac{a_n}{n^s} \), where \( s \) is a complex variable and \( a_n \) are complex coefficients, primarily used in number theory and complex analysis. While Taylor series focus on function expansions in powers of \( (x - a) \), Dirichlet series emphasize multiplicative structures and convergence in half-planes of the complex plane.
Historical Development
Taylor series, introduced by Brook Taylor in the early 18th century, marked a breakthrough in approximating functions through infinite polynomial expansions centered around a point. Dirichlet series emerged in the 19th century, formulated by Johann Peter Gustav Lejeune Dirichlet, primarily to study number-theoretic functions and prime distributions using infinite sums of the form a_n n^(-s). The historical development of Taylor series laid foundational analysis tools, while Dirichlet series advanced analytic number theory by connecting complex analysis with arithmetic progressions and L-functions.
Mathematical Formulation
Taylor series represent functions as infinite sums of power terms centered at a point, expressed as f(x) = S (f(n)(a)/n!) (x - a)n, where f(n)(a) denotes the nth derivative of f at a. Dirichlet series take the form D(s) = S an / ns, summing coefficients an weighted by n raised to a complex variable s, often used in analytic number theory. While Taylor series expand functions in terms of powers of variables, Dirichlet series utilize exponentials indexed by integers, highlighting distinct applications and convergence properties.
Convergence Properties
Taylor series converge within a radius determined by the nearest singularity of the function, exhibiting uniform convergence inside this disk. Dirichlet series, commonly expressed as sums of the form \( \sum a_n n^{-s} \), have convergence properties tied to the real part of the complex variable \( s \), converging absolutely in half-planes where the real part exceeds a critical abscissa of convergence. The analytic continuation and boundary behavior differ significantly, with Dirichlet series often requiring advanced techniques like Perron's formula or Tauberian theorems to study convergence on critical lines.
Domains of Application
Taylor series excel in approximating analytic functions within complex analysis, enabling solutions for differential equations, physics problems, and engineering models near a point of expansion. Dirichlet series find primary application in number theory and analytic number theory, particularly in studying properties of arithmetic functions and distribution of prime numbers through L-functions and the Riemann zeta function. The distinct domain of each series reflects their mathematical structure: Taylor series rely on power series expansions convergent in complex neighborhoods, while Dirichlet series converge in half-planes related to complex variables with real parts exceeding certain bounds.
Key Differences
Taylor series represent functions as infinite sums of powers of a variable, primarily used for analytic functions with complex or real arguments, while Dirichlet series express functions as infinite sums of terms involving the reciprocal of integers raised to a complex power, commonly applied in number theory. Taylor series converge within a radius determined by the nearest singularity of the function, whereas Dirichlet series convergence depends on the real part of the complex variable exceeding a certain boundary. Key differences lie in their domains of application, convergence criteria, and the nature of their terms: polynomial powers for Taylor series versus multiplicative inverse powers for Dirichlet series.
Notable Examples
Taylor series, such as the exponential function \( e^x = \sum_{n=0}^\infty \frac{x^n}{n!} \), provide power series expansions centered around a point, offering local approximations of analytic functions. Dirichlet series, exemplified by the Riemann zeta function \( \zeta(s) = \sum_{n=1}^\infty \frac{1}{n^s} \), represent infinite sums indexed by positive integers and are crucial in analytic number theory. These notable examples highlight Taylor series in complex analysis and Dirichlet series in the study of prime distributions and L-functions.
Impact on Mathematical Analysis
Taylor series provide powerful tools for approximating analytic functions through infinite polynomial expansions, significantly advancing the study of function behavior near points of convergence in complex analysis. Dirichlet series, particularly prominent in number theory and complex analysis, enable deep exploration of arithmetic functions and prime number distributions via their convergence properties and analytic continuation. The interplay between Taylor and Dirichlet series enriches mathematical analysis by connecting local function approximation with global number-theoretic structures, fostering advancements in analytic number theory and complex function theory.
Conclusion and Future Perspectives
Taylor series provide powerful tools for approximating analytic functions through power series expansions around a point, with wide applications in calculus and complex analysis. Dirichlet series, characterized by infinite sums of the form a_n/n^s, play a pivotal role in number theory and the distribution of prime numbers, especially in the study of L-functions and the Riemann zeta function. Future research may explore deeper connections between these series frameworks, leveraging advances in analytic number theory and computational methods to refine function approximations and investigate unresolved problems such as the Riemann Hypothesis.
Taylor series Infographic
 libterm.com
libterm.com