The Tor functor is a fundamental tool in homological algebra that measures the extent to which tensor products fail to be exact. It arises naturally in the study of modules over rings and provides insights into projective resolutions and extension problems. Explore this article further to deepen your understanding of the Tor functor and its applications in algebra.
Table of Comparison
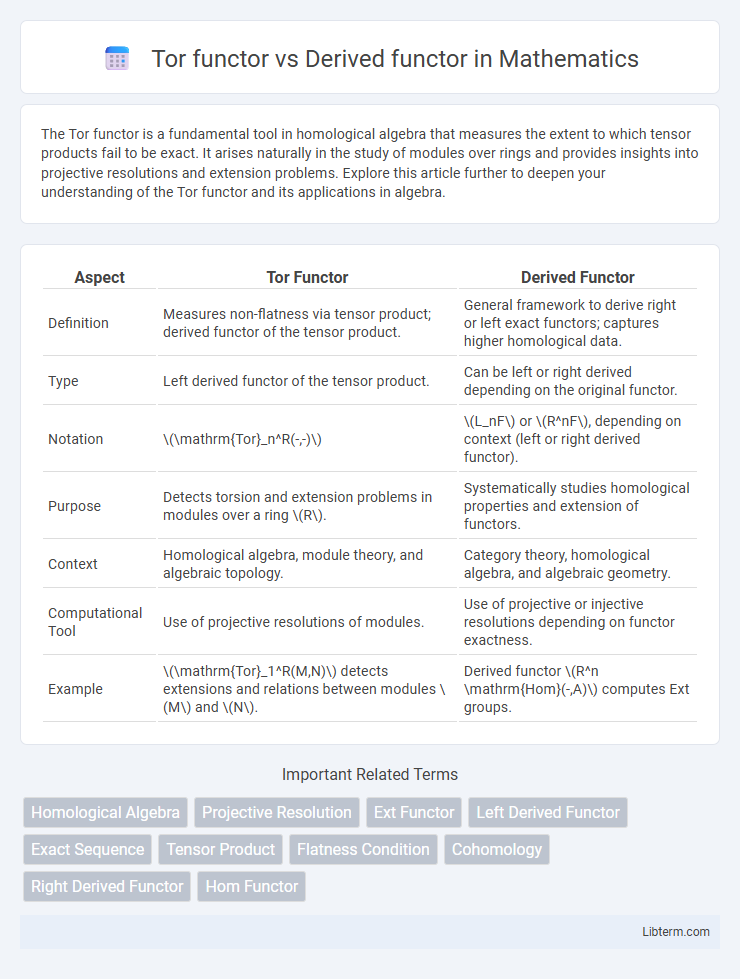
| Aspect | Tor Functor | Derived Functor |
|---|---|---|
| Definition | Measures non-flatness via tensor product; derived functor of the tensor product. | General framework to derive right or left exact functors; captures higher homological data. |
| Type | Left derived functor of the tensor product. | Can be left or right derived depending on the original functor. |
| Notation | \(\mathrm{Tor}_n^R(-,-)\) | \(L_nF\) or \(R^nF\), depending on context (left or right derived functor). |
| Purpose | Detects torsion and extension problems in modules over a ring \(R\). | Systematically studies homological properties and extension of functors. |
| Context | Homological algebra, module theory, and algebraic topology. | Category theory, homological algebra, and algebraic geometry. |
| Computational Tool | Use of projective resolutions of modules. | Use of projective or injective resolutions depending on functor exactness. |
| Example | \(\mathrm{Tor}_1^R(M,N)\) detects extensions and relations between modules \(M\) and \(N\). | Derived functor \(R^n \mathrm{Hom}(-,A)\) computes Ext groups. |
Introduction to Tor and Derived Functors
Tor functors arise in homological algebra as a fundamental tool to measure the failure of flatness of modules, capturing torsion phenomena in tensor products. Derived functors generalize classical functors by extending them to homological contexts, computing higher-order information through projective or injective resolutions. The Tor functor specifically is the left derived functor of the tensor product, revealing extensions and relations between modules beyond the zeroth level tensor product.
Fundamental Concepts of Homological Algebra
The Tor functor is a specific example of a derived functor that measures the failure of flatness in the tensor product of modules, playing a critical role in homological algebra by detecting extensions and torsion. Derived functors arise by applying homological algebra techniques to exact functors, enabling the computation of higher-dimensional invariants such as Ext and Tor groups. Both concepts are foundational in understanding the relationships between modules, exact sequences, and chain complexes within the framework of homological algebra.
Definition and Role of Tor Functor
The Tor functor, denoted as Tor_n^R(-,-), is a specific type of derived functor arising from the tensor product functor in homological algebra, measuring the failure of flatness between modules over a ring R. It captures obstruction to exactness when tensoring two R-modules, playing a crucial role in computing homology and detecting torsion phenomena. Derived functors generalize this concept by systematically extending non-exact functors to their higher-dimensional homological counterparts, with the Tor functor serving as a primary example focused on tensor products.
Overview of Derived Functors
Derived functors generalize classical functors by measuring the failure of exactness, revealing deeper homological properties in categories like modules over rings. They arise from resolving objects via projective or injective resolutions to systematically compute Ext, Tor, and other related invariants. The Tor functor is a specific derived functor of the tensor product, capturing information about how tensoring interacts with non-flat modules and providing insights into module extensions and torsion phenomena.
Key Differences: Tor Functor vs. Derived Functor
The Tor functor specifically measures the failure of flatness in modules and arises as the left derived functor of the tensor product, capturing information about torsion in homological algebra. Derived functors, a broader category, generalize the process of deriving functors beyond tensor products to include Ext, Hom, and global section functors, providing tools to compute homology and cohomology in abelian categories. While Tor focuses on tensor-related homology, derived functors encompass a wider range of constructions essential for studying exactness properties across various functors in derived categories.
Computation: How Tor Functors Are Calculated
Tor functors are computed using projective resolutions of modules, where the tensor product of a projective resolution of one module with another module is taken, and the homology of the resulting complex is studied. Specifically, the nth Tor functor \(\mathrm{Tor}_n^R(M, N)\) is the nth homology group of the complex obtained by tensoring a projective resolution of \(M\) with \(N\). Derived functors extend this process by systematically applying the original functor to resolutions and extracting homological information, making Tor a particular example specialized for tensor products.
Applications of Derived Functors in Algebra
Derived functors extend the reach of homological algebra by generalizing classical functors such as Tor, providing deep insights into module theory, sheaf cohomology, and extension groups. In algebra, derived functors play a crucial role in computing Ext and Tor groups, which measure the failure of exactness in tensor products and homomorphisms, thereby classifying extensions and detecting obstructions. Applications include resolving modules, analyzing depth and projective dimensions, and facilitating the study of spectral sequences and long exact sequences in cohomology theories.
Examples Illustrating Tor and Derived Functors
The Tor functor provides a systematic way to measure the failure of flatness in tensor products, with classic examples including Tor_1^R(M,N) capturing torsion phenomena in modules over a ring R, such as Tor_1^Z(Z/nZ, Z/mZ) Z/gcd(n,m)Z. Derived functors extend this concept by generalizing homological constructions like Ext and Tor, computed via projective or injective resolutions; for instance, Ext^n_R(M, N) arises from the right-derived functors of Hom_R, revealing extension classes and higher-order relations. Concrete cases include calculating Tor and Ext over polynomial rings or group algebras, illustrating connections between algebraic topology, module theory, and cohomological dimensions.
Importance of Exact Sequences in Functor Derivation
Exact sequences play a crucial role in the derivation of functors, serving as foundational tools to measure the failure of exactness in functors such as the Tor functor. The Tor functor arises specifically from applying the tensor product functor to projective resolutions, capturing information about extensions in homological algebra, thus providing insight into the structure of modules over rings. Derived functors generalize this concept by systematically constructing sequences that extend a given functor to higher dimensions, using exact sequences to preserve homological properties and extract deeper algebraic invariants.
Summary and Comparative Insights
The Tor functor, a specific example of a derived functor, measures the failure of flatness in module tensor products and provides information about extensions and syzygies. Derived functors generalize this concept by extending homological algebra operations, such as Ext and Tor, to derived categories for a broader class of functors. While Tor focuses on tensor product-related exactness, derived functors encompass a wider range of homological phenomena, offering a comprehensive framework for studying complex algebraic structures.
Tor functor Infographic
 libterm.com
libterm.com