Constant mean curvature surfaces exhibit uniform curvature at every point, making them critical examples in differential geometry and mathematical physics. These surfaces often arise in applications like modeling soap films, where surface tension creates equilibria with constant mean curvature. Explore the rest of the article to understand how these surfaces influence both theoretical mathematics and practical phenomena in your studies or projects.
Table of Comparison
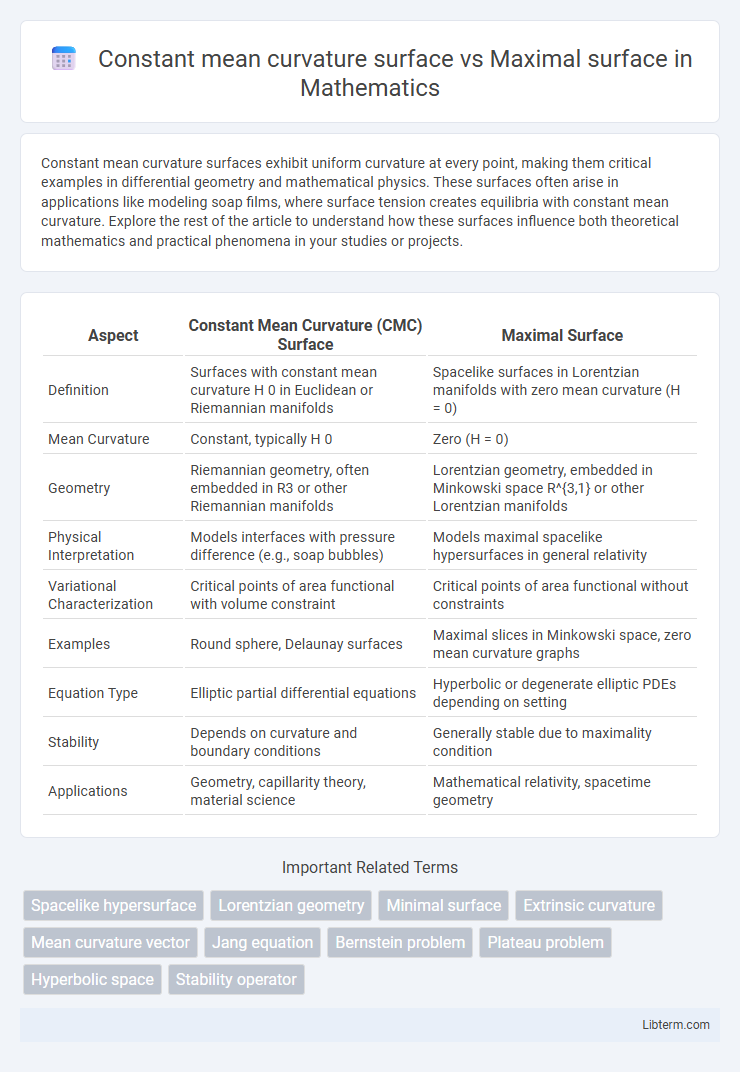
| Aspect | Constant Mean Curvature (CMC) Surface | Maximal Surface |
|---|---|---|
| Definition | Surfaces with constant mean curvature H 0 in Euclidean or Riemannian manifolds | Spacelike surfaces in Lorentzian manifolds with zero mean curvature (H = 0) |
| Mean Curvature | Constant, typically H 0 | Zero (H = 0) |
| Geometry | Riemannian geometry, often embedded in R3 or other Riemannian manifolds | Lorentzian geometry, embedded in Minkowski space R^{3,1} or other Lorentzian manifolds |
| Physical Interpretation | Models interfaces with pressure difference (e.g., soap bubbles) | Models maximal spacelike hypersurfaces in general relativity |
| Variational Characterization | Critical points of area functional with volume constraint | Critical points of area functional without constraints |
| Examples | Round sphere, Delaunay surfaces | Maximal slices in Minkowski space, zero mean curvature graphs |
| Equation Type | Elliptic partial differential equations | Hyperbolic or degenerate elliptic PDEs depending on setting |
| Stability | Depends on curvature and boundary conditions | Generally stable due to maximality condition |
| Applications | Geometry, capillarity theory, material science | Mathematical relativity, spacetime geometry |
Introduction to Constant Mean Curvature Surfaces
Constant mean curvature (CMC) surfaces are characterized by having a uniform mean curvature at every point, making them critical in differential geometry and physical applications such as soap films and bubbles. These surfaces generalize minimal surfaces, which have zero mean curvature, by allowing a nonzero constant value, thus exhibiting richer geometric properties. Unlike maximal surfaces, which arise in Lorentzian geometry with mean curvature zero in a spacelike setting, CMC surfaces often occur in Riemannian manifolds and provide insights into stability and shape optimization problems.
Defining Maximal Surfaces: An Overview
Maximal surfaces are spacelike hypersurfaces in Lorentzian manifolds characterized by zero mean curvature, representing critical points of the area functional under compactly supported variations. Unlike constant mean curvature (CMC) surfaces that maintain a nonzero constant mean curvature, maximal surfaces belong to the class of zero mean curvature surfaces, playing a significant role in general relativity and the theory of minimal surfaces in Minkowski space. Their geometry and variational properties distinguish them from CMC surfaces by balancing intrinsic curvature conditions with the causal structure of the ambient spacetime.
Key Differences Between CMC and Maximal Surfaces
Constant mean curvature (CMC) surfaces maintain a uniform mean curvature value, typically representing soap films or bubbles, while maximal surfaces are defined as spacelike surfaces in Minkowski space with zero mean curvature, corresponding to critical points of the area functional under Lorentzian metrics. The key differences include the ambient space geometry--Euclidean for CMC surfaces versus Lorentzian for maximal surfaces--and their geometric interpretations, where CMC surfaces model equilibrium shapes under constant pressure, whereas maximal surfaces describe maximal area spacelike hypersurfaces in relativity. Analytical distinctions arise from their governing equations: CMC surfaces satisfy a nonlinear elliptic partial differential equation, whereas maximal surfaces solve a hyperbolic equation related to the Minkowski metric.
Mathematical Formulation of Constant Mean Curvature
Constant mean curvature (CMC) surfaces are characterized by a uniform mean curvature H, mathematically expressed as H = (k1 + k2)/2, where k1 and k2 are the principal curvatures, satisfying the differential equation Dx = 2H N, with D representing the Laplace-Beltrami operator and N the unit normal vector. In contrast, maximal surfaces in Lorentzian geometry have zero mean curvature (H=0) and arise as critical points of the area functional in Minkowski space, defined by the vanishing mean curvature vector field. The mathematical formulation of CMC surfaces involves solving nonlinear elliptic partial differential equations, often framed as the prescribed mean curvature equation, which balances geometric curvature constraints with boundary conditions to determine the surface shape.
Geometric Properties of Maximal Surfaces
Maximal surfaces in Lorentzian geometry exhibit zero mean curvature, making them the Lorentzian analogs of minimal surfaces in Euclidean space, contrasting with constant mean curvature (CMC) surfaces that maintain nonzero constant mean curvature. These surfaces are spacelike hypersurfaces characterized by locally maximizing area, with their geometry governed by the vanishing of the trace of the second fundamental form. Unlike CMC surfaces, maximal surfaces possess unique geometric properties such as being critical points of the area functional under compactly supported variations, linking closely to solutions of the maximal surface equation in Minkowski space.
Examples of CMC and Maximal Surfaces in Geometry
Constant mean curvature (CMC) surfaces include classic examples such as the sphere, which has positive constant mean curvature, and the cylinder, characterized by zero Gaussian curvature but nonzero constant mean curvature. Maximal surfaces arise primarily in Lorentzian geometry and are exemplified by the maximal slice of the Minkowski space, where the mean curvature vanishes identically, reflecting a critical point of the area functional under Lorentzian metrics. Both surface types play crucial roles in differential geometry and general relativity, illustrating distinct geometric and physical properties.
Applications in Differential Geometry and Physics
Constant mean curvature (CMC) surfaces play a crucial role in differential geometry and physics by modeling interfaces with uniform pressure, such as soap films and bubbles, and contribute to the study of minimal energy configurations in materials science. Maximal surfaces, characterized as spacelike surfaces with zero mean curvature in Minkowski space, are fundamental in general relativity for understanding spacetime foliation and the initial value problem in cosmology. Both surface types provide essential insights into geometric analysis, with CMC surfaces influencing capillarity theory and geometric flows, while maximal surfaces offer solutions to variational problems in Lorentzian manifolds.
Stability and Uniqueness Results
Constant mean curvature (CMC) surfaces exhibit stability characteristics governed by the second variation of area under volume-preserving deformations, with uniqueness results often depending on curvature bounds and boundary conditions in embedded domains. Maximal surfaces, defined as zero mean curvature spacelike hypersurfaces in Lorentzian manifolds, display strong stability linked to their variational characterization as critical points of the volume functional in Minkowski space, with uniqueness typically constrained by causal or asymptotic conditions. Both classes of surfaces serve as critical points of geometric functionals, but the elliptic nature of CMC equations contrasts with the hyperbolic behavior in maximal surface theory impacting their respective stability and uniqueness frameworks.
Challenges in Analyzing CMC vs Maximal Surfaces
Challenges in analyzing Constant Mean Curvature (CMC) surfaces and Maximal surfaces primarily arise from their differing geometric and variational properties; CMC surfaces exhibit uniform mean curvature in Riemannian manifolds, whereas Maximal surfaces maximize area in Lorentzian manifolds with zero mean curvature. The nonlinearity of the prescribed mean curvature equation for CMC surfaces complicates existence and regularity results, while Maximal surfaces face difficulties due to their Lorentzian signature, causing potential issues with hyperbolic-type partial differential equations. Understanding the stability, singularity formation, and global behavior in both contexts requires advanced geometric analysis and PDE techniques tailored to their unique curvature constraints and ambient space structures.
Future Directions and Open Problems
Future research on constant mean curvature (CMC) surfaces explores classification in higher-dimensional Riemannian manifolds and their stability under geometric flows. Maximal surfaces, important in Lorentzian geometry, present open problems regarding their global behavior in spacetimes with non-trivial topology and singularity formation. Advancing numerical methods and employing integrable systems could bridge analytic and geometric approaches, fostering deeper understanding of both CMC and maximal surfaces.
Constant mean curvature surface Infographic
 libterm.com
libterm.com