A generalized solution provides a versatile framework applicable across multiple scenarios, enhancing problem-solving efficiency by addressing a wider range of cases. Such solutions streamline processes and reduce the need for case-by-case adjustments, saving valuable time and resources. Explore the rest of the article to discover how implementing a generalized solution can transform your approach and deliver consistent results.
Table of Comparison
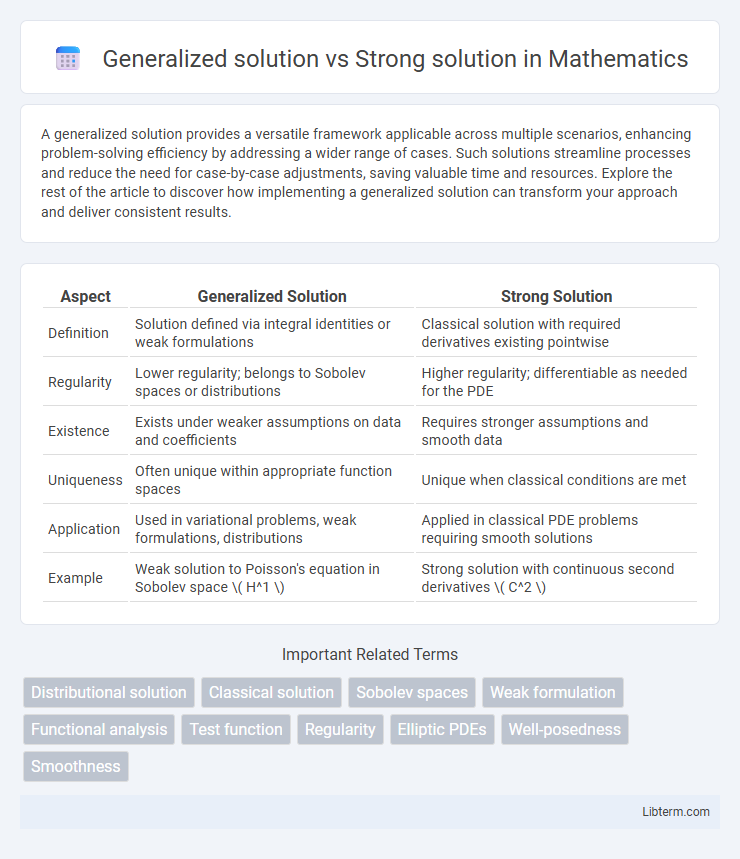
| Aspect | Generalized Solution | Strong Solution |
|---|---|---|
| Definition | Solution defined via integral identities or weak formulations | Classical solution with required derivatives existing pointwise |
| Regularity | Lower regularity; belongs to Sobolev spaces or distributions | Higher regularity; differentiable as needed for the PDE |
| Existence | Exists under weaker assumptions on data and coefficients | Requires stronger assumptions and smooth data |
| Uniqueness | Often unique within appropriate function spaces | Unique when classical conditions are met |
| Application | Used in variational problems, weak formulations, distributions | Applied in classical PDE problems requiring smooth solutions |
| Example | Weak solution to Poisson's equation in Sobolev space \( H^1 \) | Strong solution with continuous second derivatives \( C^2 \) |
Introduction to Solution Concepts in Differential Equations
Generalized solutions extend the classical framework of differential equations by allowing functions that may not possess traditional derivatives but satisfy the equation in an integral or weak sense, broadening the scope of solvable problems. Strong solutions require stricter regularity conditions, ensuring the function and its derivatives exist almost everywhere and satisfy the differential equation pointwise. Understanding the distinction between generalized and strong solutions is crucial in partial differential equations, especially when addressing existence, uniqueness, and stability of solutions in various functional spaces.
Defining Strong Solutions
A strong solution to a stochastic differential equation (SDE) is defined on a probability space equipped with a given Brownian motion, where the solution process is adapted to the filtration generated by that Brownian motion and satisfies the equation almost surely. In contrast, a generalized or weak solution allows the underlying probability space and Brownian motion to be part of the solution, meaning the filtration and noise may be constructed alongside the solution process. Strong solutions provide pathwise uniqueness and depend on a fixed stochastic basis, making them crucial for applications requiring explicit sample path representations.
Understanding Generalized (Weak) Solutions
Generalized (weak) solutions extend the concept of classical solutions by allowing functions that may not be differentiable in the traditional sense but satisfy differential equations in an integral or distributional form, crucial for handling irregular data or domains. These solutions leverage Sobolev spaces and test functions, enabling the formulation of partial differential equations where strong solutions may not exist due to irregular boundaries or discontinuities. Understanding weak solutions is key in mathematical analysis and numerical methods, as they provide a rigorous framework for existence, uniqueness, and approximation of solutions in complex real-world problems.
Key Differences Between Generalized and Strong Solutions
Generalized solutions, also known as weak solutions, extend the notion of solutions to differential equations by relaxing smoothness requirements, allowing functions that satisfy the equations in an integral or distributional sense rather than pointwise. Strong solutions require higher regularity, meaning the function must be differentiable enough to satisfy the differential equation directly almost everywhere. The key differences between generalized and strong solutions lie in existence and uniqueness conditions, regularity assumptions, and the types of boundary or initial conditions they can accommodate.
Existence and Uniqueness: Strong vs Generalized Solutions
Strong solutions to differential equations require the solution to be sufficiently smooth and satisfy the equation pointwise, ensuring both existence and uniqueness under well-defined conditions like Lipschitz continuity. Generalized solutions broaden the concept by allowing functions that satisfy the equation in an integral or weak sense, often ensuring existence when strong solutions may not be attainable, but uniqueness can be weaker or require additional constraints. PDE theory often utilizes generalized solutions to address existence in complex domains, while strong solutions guarantee more regularity and unique behavior in classical frameworks.
Regularity Requirements and Function Spaces
Strong solutions to partial differential equations require higher regularity, typically belonging to Sobolev spaces \( H^k \) with integer \( k \geq 1 \), ensuring classical differentiability and satisfying the equation pointwise. Generalized solutions, or weak solutions, reside in lower-regularity function spaces such as \( L^2 \) or \( H^1 \), where derivatives are understood in the distributional sense, allowing for solutions that lack classical differentiability but satisfy the equation in an integral form. This distinction in function spaces reflects the relaxation of regularity requirements, enabling generalized solutions to address broader classes of PDEs where strong solutions may not exist.
Applications of Strong Solutions
Strong solutions are frequently applied in stochastic differential equations (SDEs) where pathwise uniqueness and measurability with respect to a given Brownian motion are critical, such as in financial mathematics for option pricing models and risk management. They provide explicit constructions of solutions that depend continuously on the driving noise, making them essential in filtering theory and stochastic control problems. Strong solutions also ensure stability in numerical simulations, allowing accurate modeling in engineering and physics where random perturbations influence system dynamics.
Applications of Generalized Solutions
Generalized solutions play a crucial role in solving partial differential equations (PDEs) where classical (strong) solutions may not exist due to irregularities or discontinuities in boundary conditions or coefficients. They are extensively applied in fields such as fluid dynamics, quantum mechanics, and material science to model phenomena involving shock waves, turbulence, or singularities. The flexibility of generalized solutions in accommodating weak derivatives allows numerical methods like finite element and finite volume schemes to approximate solutions in complex, real-world scenarios.
Transitioning from Generalized to Strong Solutions
Transitioning from generalized solutions to strong solutions in partial differential equations requires verifying additional regularity conditions and ensuring classical differentiability almost everywhere. Strong solutions often demand stricter integrability and smoothness criteria, allowing the application of standard differential operators and facilitating uniqueness and stability analyses. Techniques such as mollification or approximation methods help bridge the gap by improving solution regularity while preserving convergence in appropriate Sobolev spaces.
Summary: Choosing the Appropriate Solution Concept
Generalized solutions extend solvability to broader function spaces, accommodating irregular data or weak differentiability, making them suitable for complex partial differential equations. Strong solutions require higher regularity and satisfy the equation pointwise, providing more precise and classical interpretations when smoothness conditions hold. Selecting between generalized and strong solutions depends on the problem's regularity, data smoothness, and desired solution properties, balancing existence with interpretability.
Generalized solution Infographic
 libterm.com
libterm.com