An open set is a fundamental concept in topology, defined as a set where every point has a neighborhood entirely contained within the set, ensuring no boundary points are included. Understanding open sets is crucial for grasping more advanced topics like continuity, convergence, and metric spaces in mathematical analysis. Explore the rest of the article to deepen your understanding of open sets and their significance in various mathematical contexts.
Table of Comparison
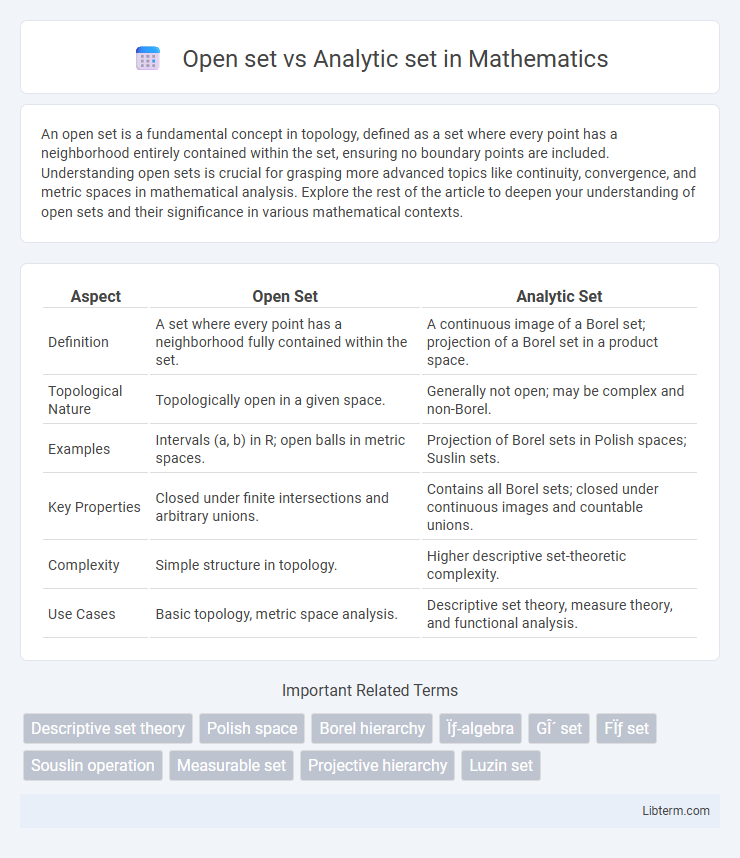
| Aspect | Open Set | Analytic Set |
|---|---|---|
| Definition | A set where every point has a neighborhood fully contained within the set. | A continuous image of a Borel set; projection of a Borel set in a product space. |
| Topological Nature | Topologically open in a given space. | Generally not open; may be complex and non-Borel. |
| Examples | Intervals (a, b) in R; open balls in metric spaces. | Projection of Borel sets in Polish spaces; Suslin sets. |
| Key Properties | Closed under finite intersections and arbitrary unions. | Contains all Borel sets; closed under continuous images and countable unions. |
| Complexity | Simple structure in topology. | Higher descriptive set-theoretic complexity. |
| Use Cases | Basic topology, metric space analysis. | Descriptive set theory, measure theory, and functional analysis. |
Introduction to Open Sets and Analytic Sets
Open sets form the foundation of topology and analysis, defined by containing an open neighborhood around each of their points within a given space. Analytic sets, arising from descriptive set theory, extend beyond Borel sets as continuous images of Borel sets in Polish spaces, capturing complex measurable structures. The distinction lies in the topological basis of open sets versus the definability and measurability properties central to analytic sets.
Definitions: What Is an Open Set?
An open set in topology refers to a collection of points within a space where each point has a neighborhood entirely contained within the set, ensuring no boundary points are included. Analytic sets, also known as Suslin sets, are projections of Borel sets in a product space and generally encompass more complex structures than open sets. Understanding these definitions highlights the topological simplicity of open sets compared to the descriptive complexity of analytic sets.
Definitions: What Is an Analytic Set?
An analytic set is a subset of a Polish space that can be represented as the continuous image of a Borel set from another Polish space, making it more general than an open set which is defined by the topology of the space as a union of open balls. Unlike open sets, analytic sets need not be open or even Borel, but they maintain measurability and have well-defined descriptive set-theoretic properties. Analytic sets play a crucial role in advanced topology and descriptive set theory by extending the concept of definable sets beyond Borel structures.
Key Differences Between Open and Analytic Sets
Open sets are fundamental in topology, defined as collections of points where each point has a surrounding neighborhood fully contained within the set, primarily used to describe continuity and convergence. Analytic sets, originating from descriptive set theory, are more complex, often constructed as continuous images of Borel sets in Polish spaces, and can be non-Borel, making them crucial in advanced measure theory and logic. The key difference lies in their definitional complexity and topological properties: open sets are topologically simple and explicitly definable, while analytic sets capture a broader class of sets that may lack openness but retain measurability and definability attributes.
Topological Properties of Open Sets
Open sets, fundamental in topology, are characterized by containing an open neighborhood around each of their points, ensuring local stability and continuity. Analytic sets, broader in scope, are images of Borel sets under continuous mappings and may lack the 'local openness' property inherent to open sets. The topological properties of open sets include closure under arbitrary unions and finite intersections, while analytic sets exhibit complexities related to measurability and descriptive set theory, influencing their classification beyond standard open set behavior.
Descriptive Set Theory and Analytic Sets
In Descriptive Set Theory, open sets form the foundation of the Borel hierarchy, representing the simplest definable sets in Polish spaces, while analytic sets extend these by including continuous images of Borel sets, thus capturing a broader class beyond Borel sets. Analytic sets, also known as S1^1 sets, are significant for their closure properties under projections and continuous preimages, making them crucial in classifying definable subsets of Polish spaces. Unlike open sets, analytic sets can be non-Borel, highlighting the complexity and richness of definable sets in descriptive set-theoretic analysis.
Examples Illustrating Open Sets
Open sets in topology include intervals such as (0,1) in the real numbers, where every point has a neighborhood fully contained within the set. For example, the union of open intervals (0,1) and (2,3) represents an open set in the real line, demonstrating how open sets can be disjoint yet collectively open. Analytic sets, by contrast, arise in descriptive set theory and can be more complex, including projections of Borel sets, and do not necessarily exhibit the simple neighborhood properties characterizing open sets.
Examples Illustrating Analytic Sets
Analytic sets include projections of Borel sets and are more complex than open sets, which are the simplest examples of Borel sets. For instance, the continuous image of a Borel set in a Polish space is an analytic set but not necessarily open, illustrating that analytic sets extend beyond classical open sets. Examples such as the projection of a Borel subset of the plane onto the real line highlight how analytic sets capture more intricate topological properties than open sets.
Applications: Open Sets vs Analytic Sets
Open sets play a fundamental role in topology, metric spaces, and functional analysis, serving as building blocks for defining continuity, convergence, and differentiability. Analytic sets, a broader class including Borel sets, are crucial in descriptive set theory and measure theory, often applied in probability theory, ergodic theory, and the study of complex dynamic systems. The distinction impacts applications such as defining measurable functions, characterizing projective hierarchies, and solving selection problems in mathematical analysis.
Summary and Final Comparison
Open sets in topology are defined by the property that every point within the set has a neighborhood entirely contained in the set, forming the foundational building blocks for topological spaces. Analytic sets, arising in descriptive set theory, are continuous images of Borel sets in Polish spaces and often exhibit complex, non-Borel characteristics while remaining measurable. The key distinction lies in their complexity and definability: open sets are simple and well-understood, whereas analytic sets generalize Borel sets and capture more intricate structures beyond standard open or closed sets.
Open set Infographic
 libterm.com
libterm.com