A measurable set is a fundamental concept in measure theory, allowing the assignment of a consistent size or volume to subsets within a given space. This property is crucial for integrating functions and analyzing probabilities in mathematical contexts. Explore the rest of the article to understand how measurable sets enable rigorous mathematical analysis and their applications in various fields.
Table of Comparison
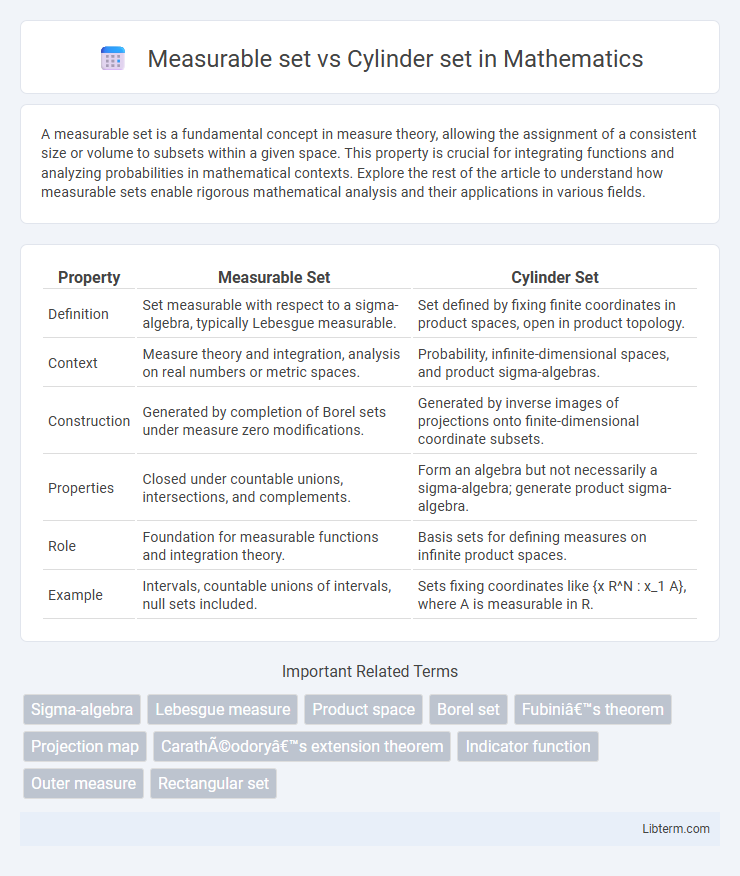
| Property | Measurable Set | Cylinder Set |
|---|---|---|
| Definition | Set measurable with respect to a sigma-algebra, typically Lebesgue measurable. | Set defined by fixing finite coordinates in product spaces, open in product topology. |
| Context | Measure theory and integration, analysis on real numbers or metric spaces. | Probability, infinite-dimensional spaces, and product sigma-algebras. |
| Construction | Generated by completion of Borel sets under measure zero modifications. | Generated by inverse images of projections onto finite-dimensional coordinate subsets. |
| Properties | Closed under countable unions, intersections, and complements. | Form an algebra but not necessarily a sigma-algebra; generate product sigma-algebra. |
| Role | Foundation for measurable functions and integration theory. | Basis sets for defining measures on infinite product spaces. |
| Example | Intervals, countable unions of intervals, null sets included. | Sets fixing coordinates like {x R^N : x_1 A}, where A is measurable in R. |
Introduction to Measurable Sets and Cylinder Sets
Measurable sets are fundamental in measure theory, defined within a sigma-algebra that allows consistent assignment of measures, ensuring properties like countable additivity. Cylinder sets serve as basic building blocks in product spaces, constructed by fixing coordinates in finite dimensions and extending across others, often used to generate sigma-algebras on infinite-dimensional spaces. Distinguishing measurable sets from cylinder sets is crucial for understanding measure construction and integration in advanced probability and functional analysis.
Fundamental Concepts in Measure Theory
Measurable sets form the core of measure theory, defined within a sigma-algebra that allows consistent assignment of measures to sets. Cylinder sets serve as elementary building blocks, especially in product spaces, generated by fixing coordinates in finite dimensions and extended via completion to measurable sets. Understanding the interplay between cylinder sets and measurable sets is crucial in constructing product measures and handling infinite-dimensional spaces in measure theory.
Defining Measurable Sets: Key Properties
Measurable sets are defined within a sigma-algebra, ensuring closure under countable unions, intersections, and complements, which guarantees well-defined measures. Cylinder sets serve as generating sets for the sigma-algebra on product spaces, forming a basis for defining measurable sets through countable operations. Key properties of measurable sets include measurability under projection maps and stability under operations critical for measure construction and integration.
What is a Cylinder Set?
A cylinder set is a fundamental construct in the product sigma-algebra, defined as the preimage of a measurable set under the projection map from an infinite product space onto a finite-dimensional coordinate subspace. It captures finite-dimensional "slices" of sequences or functions, serving as building blocks for measurable sets in spaces like sequence spaces or function spaces. Measurable sets in these product spaces are generated by countable unions, intersections, and complements of cylinder sets, ensuring sigma-algebra properties.
Notation and Construction of Cylinder Sets
Cylinder sets in measure theory are typically denoted as \( C = \{ \omega \in \Omega : (\omega_{i_1}, \omega_{i_2}, \ldots, \omega_{i_k}) \in A \} \), where \( A \) is a measurable subset of a finite product space and \( \{i_1, i_2, \ldots, i_k\} \) indexes finite coordinates. These sets form the base for the product s-algebra and their construction involves identifying fixed coordinates with measurable constraints, enabling the extension to measurable sets in infinite-dimensional spaces. Measurable sets are generated as the s-algebra closure of such cylinder sets, ensuring compatibility with the underlying measure structure.
Measurability of Cylinder Sets
Cylinder sets serve as foundational building blocks in product sigma-algebras, defined by fixing coordinates on finitely many dimensions while allowing variation elsewhere. The measurability of cylinder sets is guaranteed since they belong to the sigma-algebra generated by these finite-dimensional coordinate projections, ensuring they are measurable in the product space. This property is crucial for constructing product measures and facilitating integration on infinite-dimensional spaces.
Comparison: Measurable Set vs Cylinder Set
Measurable sets in a sigma-algebra extend beyond cylinder sets, which are basic building blocks defined by fixing finite coordinates in product spaces. Cylinder sets are always measurable in the product sigma-algebra, but measurable sets may include more complex subsets formed through countable unions, intersections, and complements of cylinder sets. This distinction highlights that while all cylinder sets are measurable, the converse does not hold, reflecting a hierarchical relationship crucial in measure theory and probability on infinite-dimensional spaces.
Role of Cylinder Sets in Product Measures
Cylinder sets serve as the foundational building blocks in the construction of product measures by generating the product s-algebra on infinite-dimensional spaces. These sets, defined by fixing coordinates in a finite number of dimensions while allowing all others to vary freely, facilitate the extension of finite-dimensional measures to infinite product spaces through the Caratheodory extension theorem. Their role ensures that measurable sets in product spaces are well-characterized, enabling accurate integration and probability measure construction in functional analysis and stochastic processes.
Applications in Probability and Analysis
Measurable sets form the foundation of probability spaces by defining events with well-established sigma-algebras, allowing rigorous probability measures to be assigned. Cylinder sets, as finite-dimensional projections in product spaces, serve as building blocks for generating sigma-algebras on infinite-dimensional spaces, crucial in constructing stochastic processes and defining measures like Wiener and Gaussian measures. Applications in analysis include utilizing measurable sets for integration theory and leveraging cylinder sets to extend measures and analyze functional spaces in probability theory.
Summary and Key Takeaways
Measurable sets form the foundation of measure theory, enabling the rigorous assignment of measures such as length, area, or probability, while cylinder sets serve as generating elements of the product sigma-algebra in infinite-dimensional spaces, particularly in probability theory. Every cylinder set is measurable, but measurable sets include broader classes that are limits and complements of cylinder sets, ensuring closure under countable operations vital for constructing measures. Understanding the hierarchy and interaction between measurable and cylinder sets is crucial for applications in stochastic processes, functional analysis, and integration theory.
Measurable set Infographic
 libterm.com
libterm.com