Group algebra combines group theory and ring theory to create an algebraic structure that encodes group elements with coefficients from a given field or ring. This construction allows powerful methods from linear algebra and module theory to analyze the properties and representations of groups. Explore the rest of this article to deepen your understanding of how group algebras support various applications in mathematics and physics.
Table of Comparison
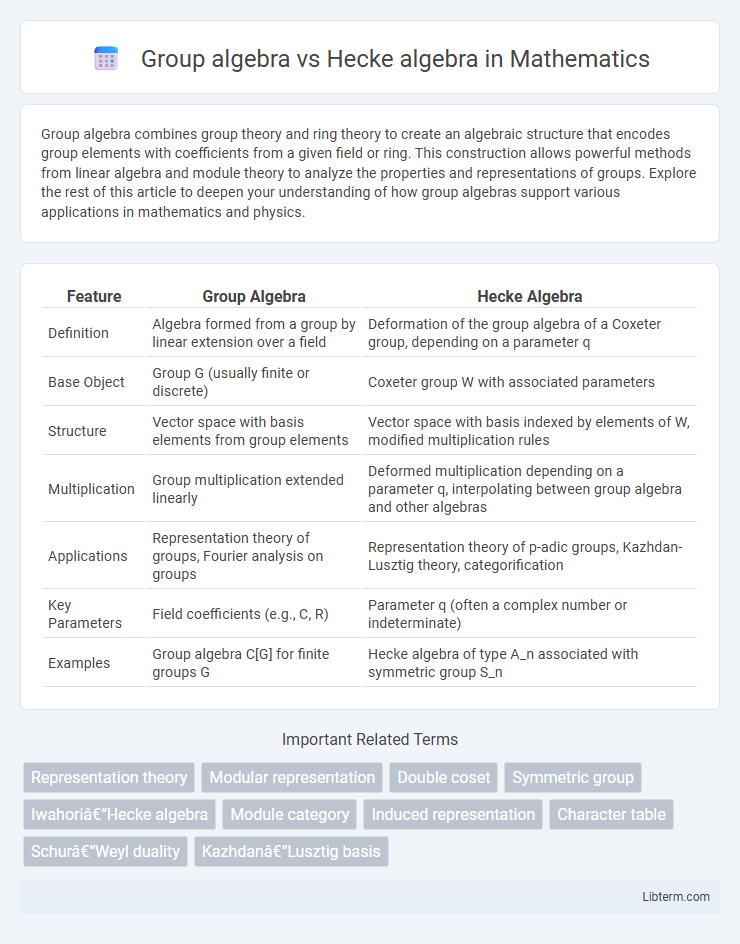
| Feature | Group Algebra | Hecke Algebra |
|---|---|---|
| Definition | Algebra formed from a group by linear extension over a field | Deformation of the group algebra of a Coxeter group, depending on a parameter q |
| Base Object | Group G (usually finite or discrete) | Coxeter group W with associated parameters |
| Structure | Vector space with basis elements from group elements | Vector space with basis indexed by elements of W, modified multiplication rules |
| Multiplication | Group multiplication extended linearly | Deformed multiplication depending on a parameter q, interpolating between group algebra and other algebras |
| Applications | Representation theory of groups, Fourier analysis on groups | Representation theory of p-adic groups, Kazhdan-Lusztig theory, categorification |
| Key Parameters | Field coefficients (e.g., C, R) | Parameter q (often a complex number or indeterminate) |
| Examples | Group algebra C[G] for finite groups G | Hecke algebra of type A_n associated with symmetric group S_n |
Introduction to Group Algebra and Hecke Algebra
Group algebra is a vector space constructed from a given group, where elements are formal linear combinations of group members with coefficients from a specified field, allowing algebraic operations that combine group structure and field properties. Hecke algebra, derived from a Coxeter group and associated with certain double coset spaces, extends group algebra concepts by incorporating deformation parameters that encode symmetries and representation-theoretic properties. Both algebras play crucial roles in representation theory, with group algebras facilitating the study of group representations over fields, while Hecke algebras provide powerful tools for analyzing modular and quantum deformations of these representations.
Algebraic Structures: Foundations and Definitions
Group algebras are algebraic structures formed by combining a group G with a field K, creating a vector space K[G] where group elements serve as a basis, and multiplication extends linearly from group operation. Hecke algebras arise as deformations of group algebras associated with Coxeter groups, equipped with a parameter q that modifies multiplication rules to incorporate representation-theoretic and combinatorial data. Both structures serve as foundational tools in algebraic representation theory, with group algebras encoding symmetries directly and Hecke algebras enriching these symmetries by incorporating weight and braid relations.
Historical Development and Origins
Group algebras originated from the study of group representations in the early 20th century, with foundational work by Richard Brauer and Issai Schur linking algebraic structures to group theory. Hecke algebras emerged later in the mid-20th century through Erich Hecke's investigations into modular forms and number theory, formalizing algebras associated with double cosets and reflecting symmetries in mathematical objects. The historical development of both structures reveals their deep roots in representation theory, with group algebras focusing on linear actions of groups and Hecke algebras extending these ideas to more complex algebraic and combinatorial settings.
Key Properties and Operations
Group algebra is constructed from a group G and a field k, forming a vector space with basis elements corresponding to group elements, enabling linear combinations and multiplication defined by group operations extended linearly. Hecke algebra generalizes this by incorporating a parameter q and certain relations tied to a Coxeter group and its associated braid group, providing a deformation of the group algebra that plays a crucial role in representation theory. Key operations in group algebras include convolution and involution, while Hecke algebras feature braid relations and quadratic relations, reflecting their richer algebraic structure and connection to geometry and combinatorics.
Comparison of Representations
Group algebra representations correspond directly to the underlying group structure, featuring modules formed over the group ring that reflect group elements' linear combinations. Hecke algebra representations arise from deformations of group algebras associated with Coxeter groups, introducing parameters that modify character theory and induce richer, parameter-dependent module categories. This results in Hecke algebra representations generalizing those of group algebras, often exhibiting intricate behavior connected to quantum groups and categorification frameworks.
Applications in Representation Theory
Group algebras provide a foundation for studying representations of finite groups by encoding group elements as basis vectors in an algebra, facilitating module analysis and character theory. Hecke algebras, arising from double coset spaces of Coxeter groups or p-adic groups, offer deformations of group algebras that enable categorifying and understanding modular representations and Kazhdan-Lusztig theory. Applications in representation theory leverage Hecke algebras to classify irreducible representations, analyze parabolic induction, and connect geometric representation theory with number theory through the Langlands program.
Role in Symmetry and Combinatorics
Group algebras encode symmetries by providing an algebraic framework for group actions, enabling the study of representations and invariants in combinatorial structures. Hecke algebras generalize group algebras by deforming the relations of Coxeter groups, playing a central role in the representation theory of symmetric groups and their quantum analogs. Both algebras facilitate the analysis of symmetry via algebraic operations and combinatorial data such as Kazhdan-Lusztig polynomials and Young tableaux.
Differences in Basis and Generators
Group algebra is formed by taking linear combinations of group elements as a basis, where each group element serves as a distinct generator, reflecting the group's underlying structure directly. Hecke algebra generalizes this by introducing generators associated with the Coxeter group elements but modifies relations through deformation parameters, producing a basis linked to double cosets that differ from the original group elements. The key difference lies in the Hecke algebra's use of parameter-dependent generators and a basis that encodes deeper algebraic and geometric properties beyond the straightforward group element basis of the group algebra.
Connections to Quantum Groups and Modular Forms
Group algebras and Hecke algebras both play crucial roles in the study of quantum groups and modular forms by providing algebraic frameworks that facilitate representation theory and symmetry analysis. Hecke algebras arise naturally in the context of p-adic groups and affine Weyl groups, serving as deformations of group algebras that capture deep connections with quantum groups through their categorification and braid group actions. The link to modular forms emerges via the Hecke operators, which act on spaces of modular forms and can be interpreted algebraically using Hecke algebras, revealing profound interactions between number theory, algebraic geometry, and quantum algebra.
Future Directions and Open Problems
Future directions in the study of group algebras and Hecke algebras emphasize the exploration of their categorical and geometric representation theories, particularly through the lens of higher representation theory and categorification. Open problems include classifying irreducible representations in modular settings, understanding the connections between Hecke algebras and quantum groups, and extending the framework to new algebraic structures arising from infinite or p-adic groups. Advances in computational approaches and homological techniques are expected to play a crucial role in resolving these challenges and uncovering deeper links between these algebras.
Group algebra Infographic
 libterm.com
libterm.com