Lebesgue measure is a fundamental concept in measure theory that assigns a consistent way to measure the size of subsets in Euclidean space, extending the notion of length, area, and volume. It is essential for integration, probability, and real analysis, enabling more complex functions and sets to be handled compared to traditional measures. Discover how Lebesgue measure can deepen your understanding of modern mathematics by exploring the rest of this article.
Table of Comparison
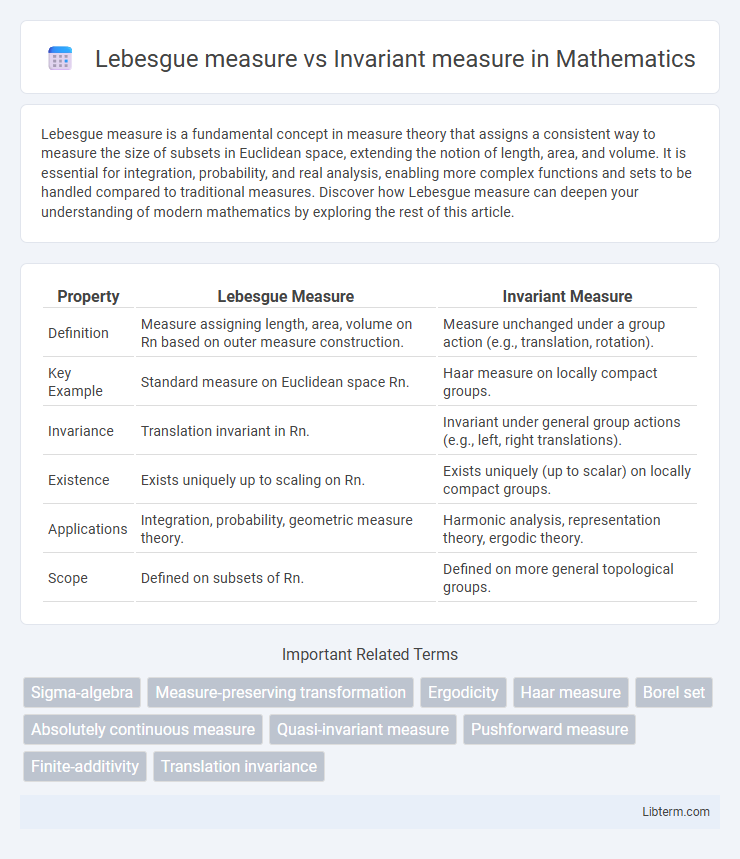
| Property | Lebesgue Measure | Invariant Measure |
|---|---|---|
| Definition | Measure assigning length, area, volume on Rn based on outer measure construction. | Measure unchanged under a group action (e.g., translation, rotation). |
| Key Example | Standard measure on Euclidean space Rn. | Haar measure on locally compact groups. |
| Invariance | Translation invariant in Rn. | Invariant under general group actions (e.g., left, right translations). |
| Existence | Exists uniquely up to scaling on Rn. | Exists uniquely (up to scalar) on locally compact groups. |
| Applications | Integration, probability, geometric measure theory. | Harmonic analysis, representation theory, ergodic theory. |
| Scope | Defined on subsets of Rn. | Defined on more general topological groups. |
Introduction to Measure Theory
In measure theory, Lebesgue measure provides a standard way to assign lengths, areas, or volumes to subsets of Euclidean space, serving as a foundation for integrating functions. Invariant measures, such as Haar measure, remain unchanged under group actions, enabling analysis on topological groups and manifolds. Understanding the distinction between Lebesgue measure's focus on geometric size and invariant measures' symmetry properties is crucial for advanced studies in analysis and probability.
Defining the Lebesgue Measure
The Lebesgue measure is a fundamental concept in measure theory, defined on the sigma-algebra of Lebesgue measurable subsets of \(\mathbb{R}^n\), assigning a non-negative real number representing the "volume" of a set. It is translation-invariant, meaning the measure of a set does not change under shifts, which distinguishes it as a standard example of an invariant measure on Euclidean spaces. Unlike more general invariant measures that may apply to group actions or manifolds, the Lebesgue measure specifically captures the intuitive notion of length, area, or volume in Euclidean geometry.
Understanding Invariant Measures
Invariant measures are fundamental in ergodic theory and dynamical systems, where they remain unchanged under the action of a transformation or group. Unlike the Lebesgue measure, which is translation-invariant on Euclidean spaces and serves as the standard measure for volume, invariant measures can be defined more broadly on abstract spaces, capturing long-term statistical behavior of orbits. Understanding invariant measures involves studying fixed points of the pushforward operator induced by a dynamical system, often leading to insights into system stability, recurrence, and ergodicity.
Key Properties of Lebesgue Measure
Lebesgue measure is a complete, translation-invariant measure defined on the s-algebra of Lebesgue measurable subsets of Rn, assigning the intuitive "volume" to sets while extending the notion of length and area. It satisfies countable additivity, meaning the measure of a countable union of disjoint sets equals the sum of their measures, and is regular, allowing approximation of measurable sets from inside by compact sets and from outside by open sets. Unlike general invariant measures, Lebesgue measure is uniquely characterized by its invariance under translations and its consistency with the standard Euclidean volume.
Fundamental Characteristics of Invariant Measures
Invariant measures maintain consistent measure values under a group action or transformation, ensuring that measurable sets are preserved in size despite changes in their position or configuration. Unlike the Lebesgue measure, which is translation-invariant specifically on Euclidean spaces, invariant measures generalize this concept to diverse structures such as topological groups or dynamical systems. Fundamental characteristics include uniqueness under certain conditions, ergodicity properties, and compatibility with symmetries or group actions, making invariant measures essential in fields like ergodic theory and harmonic analysis.
Examples of Lebesgue and Invariant Measures
The Lebesgue measure on \(\mathbb{R}^n\) assigns the standard notion of volume, length, or area, making it the prototype of a translation-invariant measure extensively used in real analysis. In contrast, invariant measures arise in dynamical systems, where for example, the Haar measure on a compact topological group remains invariant under group actions, such as rotations on the unit circle \(S^1\). Another example is the probability measure invariant under a Markov chain transition, which differs from the Lebesgue measure by encoding the system's long-term statistical behavior rather than geometric volume.
Differences Between Lebesgue and Invariant Measures
Lebesgue measure is a standard way of assigning length, area, or volume to subsets of Euclidean space, characterized by translation invariance and sigma-additivity, making it fundamental in real analysis and probability theory. Invariant measures, on the other hand, are defined relative to a transformation or group action, remaining unchanged under these transformations, which is central in ergodic theory and dynamical systems. The key difference lies in Lebesgue measure being a specific, canonical measure on Euclidean spaces, while invariant measures generalize this concept to various spaces and transformations, often lacking uniqueness and requiring construction tailored to particular group actions.
Applications in Dynamical Systems and Probability
Lebesgue measure provides a fundamental tool for quantifying volume and probability in Euclidean spaces, enabling rigorous formulation of concepts like ergodicity and mixing in dynamical systems. Invariant measures extend Lebesgue measure by remaining unchanged under the dynamics of a system, playing a crucial role in understanding long-term statistical behavior and stability of orbits. Applications in probability include characterizing stationary distributions of Markov processes and analyzing random dynamical systems through invariant probability measures linked to ergodic theorems.
Importance in Modern Analysis
Lebesgue measure plays a crucial role in modern analysis by providing a rigorous framework for integrating functions over real numbers, enabling the treatment of more complex sets than classical Riemann integration allows. Invariant measures, such as Haar measure on groups, are fundamental for studying symmetries and ergodic theory by ensuring measures remain unchanged under group actions. Both measures underpin functional analysis, probability theory, and dynamical systems, establishing foundational tools for modern mathematical research and applications.
Conclusion and Future Directions
The Lebesgue measure serves as a fundamental tool in real analysis and probability, providing a translation-invariant, complete measure on Euclidean spaces, while invariant measures extend this concept to broader settings such as dynamical systems and group actions, preserving measure under specific transformations. Future research may explore the interplay between these measures in non-Euclidean geometries, fractal sets, and ergodic theory, aiming to develop more generalized invariant measures that accommodate various symmetries and complex structures. Advancements in computational methods for invariant measure approximation and applications in statistical mechanics and quantum systems also represent promising avenues for further investigation.
Lebesgue measure Infographic
 libterm.com
libterm.com